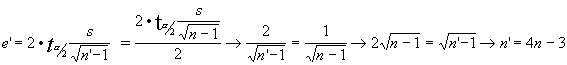1. Se van a realizar un gran y desconocido número de ensayos para calibrar la resistencia media a la rotura de un determinado azulejo en una partida de 10.000.000 de unidades. Si deseamos cometer un error inferior a 10 kg/cm2 , y por ensayos anteriores conocemos que la varianza en la rotura ha sido de 40 (kg/cm2)2 .¿Qué número de ensayos hemos de realizar si hemos decidido trabajar con un nivel de confianza del 95,5% ?

Si suponemos un gran número de ensayos ,suponemos , también, que el tamaño muestral es grande por lo que podemos establecer normalidad así el error sería :

                            dado que nos planteamos un nivel de confianza del 95,5% los valores de

                           por lo que con la información de la que disponemos tendremos que :   

tomaríamos 7 muestras o ensayos lo que evidentemente no es un gran número cómo planteaba el ejercicio.

Por otro lado no hemos usado el factor corrector de poblaciones finitas dado que podemos considerar a la población como infinita (10.000.000 unidades)

2. Para la estimación del parámetro q = m de una población cuya distribución es N[m  ;s ] siendo la desviación conocida , se elabora un intervalo de una determinada holgura y con nivel de confianza del 90% . Determinar el número de observaciones muestrales necesarias con (m.a.s.) para aumentar el nivel de confianza de dicho intervalo al 95% manteniendo , evidentemente , la misma holgura.

Estamos ante un intervalo para la media con población normal y varianza conocida
así la holgura o error será :       para el caso concreto de un nivel de confianza del 90%

     tendremos que     para el caso de nivel de confianza 95%
    tendremos que dado que según tablas

    tendremos que dado que se mantiene la holgura o error :

   

tendremos , pues que aumentar un 141% el tamaño muestral inicial para aumentar el nivel de confianza con la misma holgura.

3. Queremos conocer la diferencia entre las ventas medias diarias de dos de nuestros supermercados ubicados en ciudades distintas. Para ello obtenemos información aleatoria de 300 días de nuestro supermercado de Avila , resultando : ventas medias diarias 20 u.m. desviación típica 5 .u.m La información resultante de 250 días aleatorios en nuestro supermercado de Badajoz fue : media de ventas 15 u.m . desviación 8 u.m. . Si para conocer de diferencia entre las ventas medias construimos un intervalo de confianza con nivel de significación del 10%. Estimar el error que podemos cometer al intentar conocer dicha diferencia.

                En Avila    n=300 y S=5

               En Badajoz n=250 y S=8
            Se quiere construir un intervalo para la diferencia de medias con poblaciones
            que no son normales pero como los tamaños muestrales son grandes podemos tomarlas cómo tales.

    El error será 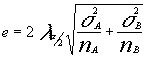          dado que los tamaños son grandes podemos tomar las varianzas poblacionales
como las muestrales , según tablas el valor de
        dado que el nivel de confianza es del 90% así el error u holgura será :

               unidades de holgura.
         el intervalo sería      con nivel de confianza del 90%

4. Para conocer la valoración en forma de porcentaje de aceptación hacia un determinado profesor decidimos encuestar a un determinado número de sus 100 alumnos. Calcular dicho número ,si el error que estamos dispuestos a admitir es del más menos 3% y trabajamos con un nivel de confianza del 95% , conociendo además, por experiencias en otras clases ,que el 5% de los alumnos se niegan a contestar.

El tamaño de la población es pequeño N=100 ,
queremos conocer el tamaño muestral n , evidentemente el muestreo ha de ser irrestricto ,

el error a cometer será de más -menos 3%
                         así :

     en nuestro caso por la tabla de la normal conocemos
    dado que el nivel de confianza con el que trabajamos es del 95% ,
    además tomaremos p=q=0,5 dado que no tenemos otra información sobre p , así :

                       

        necesitamos la información proviniente de 92 encuestas , dado que el 5% no contestan habremos de realizar más para           prever esa falta de información así :

el numero necesario será m de manera que n=m-0,05m =m(1-0,05)=m(0,95)
donde si n=96 m será 101
dado que no hay 101 alumnos tendremos que encuestarlos a todos y después recalcular el error en base a las contestadas.

5. Sean los 22500 créditos concedidos por una entidad financiera , de los que se calcula una proporción máxima de un 5% por cuantías inferiores a 250.000 pts.
Calcule la precisión que se alcanza con una confianza del 90% en la estimación de los créditos de menos de 250.000 ptas supuesta una muestra de 557 créditos

        La población de créditos es N=22500 de los que se conoce que como máximo el 5% son
        de menos de 250000 pts , la muestra es de 557 y la población podemos tomarla como finita así :
        el error (precisión en el intervalo será) :

                   
                el valor de la tabla para un nivel de confianza del 90% será 

             el valor de p lo tomaremos como 0,05 el más desfavorable posible y por tanto tendremos que
                   

6. Si queremos construir un intervalo para la media de la población con una muestra pequeña y conocemos que la población es normal pero desconocemos la varianza .¿Cuánto aumentará el tamaño muestral si nos planteamos reducir la amplitud del intervalo a la mitad, manteniendo el mismo nivel de significación ?

        Según la información que tenemos : muestra pequeña , normalidad , varianza pequeña ,
        el intervalo a construir será :

                   así el error a cometer será :

                         manteniendo nivel de significación tendremos que el error prima será :

                                   

                   
                luego tendremos que aumentar el tamaño muestral de manera que sea 4 veces el anterior menos 3