Research Lines
- Development of QM/MM strategies for the description of large systems: Dual level techniques are designed to allow a better description of the QM subsystem during the exploration of the Potential Energy Surface at a reasonable computational cost. Corrections schemes based on 2D-cubic splines have been also designed to be used during MD simulations.
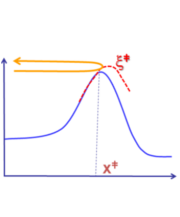
- Dynamical effects in enzymatic catalysis: We use both rare event trajectories and Grote-Hynes theory to rationalize and quantify the dynamic coupling between the reaction coordinate and the rest of degrees of freedom of the system under study.
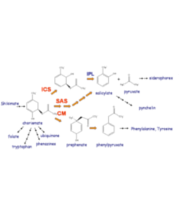
- Analysis of enzymatic reactions: the methyltransferases. This family of enzymes catalyze the methyl transfer from SAM cofactor to the substrate (a neurotranmissor, a DNA sequence, an aminoacid,…) The reaction may include both a methyl transfer and a proton transfer. Reaction mechanism are explored and free energy profiles determined.
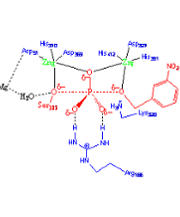
- Analysis of enzymatic reactions: the Alkaline Phosphatase family. These enzymes catalyze the alkaline hydrolysis of phosphodiesters or monoesters. Usually these enzymes also present a secondary activity catalyzing the hydrolysis of their non-natural substrates. A theoretical analysis is being carried out in order to understand how this family evolved from a common ancestror developing either diesterase or monoesterase activity.
- Computer-aided design of new biological catalysts. Our purpose is to use QM/MM-MD techniques to propose specific mutations of a particular protein in order to improve a particular activity. Chorismate rearrangement to prephenate is one of our target reactions.
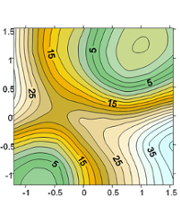
- Development of methods for localization of reaction pathways and transition states in complex chemical processes. Many chemical reactions, especially enzymatic ones, include several simultaneous reaction steps. These reactions can not be treated using a simple, intuitive reaction coordinate and require computationally expensive multidimensional sampling to obtain an adequate description. We address this issue by adapting and combining state of the art pathway based techniques, such as the String Method and path collective variables to obtain sophisticated one-dimensional reaction coordinates that provide a comparable (if not superior) performance to much more computationally demanding multidimensional techniques.