4. ESTRATEGIA DE ANÁLISIS

A la hora de llevar a cabo un proyecto de investigación es habitual, aunque afortunadamente cada vez menos, que los investigadores, una vez recogidos los datos, se acerquen a un estadístico o a una persona con conocimientos de estadística con una base de datos en un disquete con la pregunta ¿ Me puedes hacer la estadística de estos datos para ver si lo que yo pretendía averiguar se puede resolver ? . La respuesta habitual suele ser : De la forma que has recogido los datos, la cantidad de sujetos que tienes no es posible responder a lo que tu te proponías, si no otra cosa que además no tiene nada que ver con tu objetivo. Si hubieras venido antes de recoger los datos, con el mismo esfuerzo...

 El presente modulo pretende mostrar todos aquellos aspectos del análisis que deben de ser considerados en la fase de diseño de una investigación , y en concreto de una investigación cuantitativa.

Para ello como un paso previo seria conveniente que se indique cual es el papel de la estadística en el método de la investigación empírica, así como cuales son sus principales objetivos y limitaciones. 

Habitualmente a la estadística se le ha asignado un importante papel en la parte de recolección, organización y análisis de los datos, sin embargo para que esta parte este bien efectuada, como ya se ha mencionado, habrá que tener en cuenta a la estadística en la fase de diseño del estudio, e incluso en la de la formulación de las hipótesis, dado que muchas veces la hipótesis planteada puede se cambiada según la formulación estadística que se haga. Por ejemplo no es lo mismo decir que la media de la altura de los niños al nacer aumenta en la población que decir que la proporción de niños de más de 58 cm al nacimiento aumenta.

Antes de entrar a definir de forma más concreta la forma y cantidad de recoger los sujetos de estudio vale la pena considerar que es lo que la estadística puede resolver. Ante un problema de investigación, por ejemplo, cual es la prevalencia de efectos secundarios en la vacunación a los 15 meses, la solución ideal sería poder estudiar a todos los niños que se vacuna a los 15 meses y seguirlos para ver cuantos de ellos sufren efectos, lo que es imposible. Podemos suponer que para toda la población de niños de 15 meses que son vacunados existe un mecanismo de caja negra de la naturaleza que es el que indica si un niño ha de tener o no efectos secundarios. La estadística va a utilizar sus métodos para que a modo de fotocopiadora estos traten de emular los mecanismos de la naturaleza y generar unos datos inferidos , de modo que se pueda calcular cual es la distancia entre los datos observados por la naturaleza y los datos inferidos por la estadística.

Este esquema se puede observar abajo tal como realmente se lleva a cabo. A partir de la población que se desea estudiar, por ejemplo los niños de 15 meses que son vacunados, a la caja negra de la naturaleza se le suele llamar distribución de probabilidad, de modo que esta asigna a cada uno de los niños una probabilidad p de padecer efectos secundarios. Este parámetro desconocido p ,que no es más que la prevalencia poblacional de efectos secundarios, es el que se pretende que los métodos estadísticos averigüen. Para ello se obtiene una muestra de la población por las llamadas técnicas de muestreo, y se estima cual es la prevalencia de efectos en esta muestra. Si efectivamente el muestreo es aleatorio o probabilístico, se puede calcular o mejor dicho acotar cual es la distancia entre la verdadera prevalencia en la población y la obtenida a partir del uso de técnicas estadísticas de muestreo. Es lo que se llama error aleatorio.

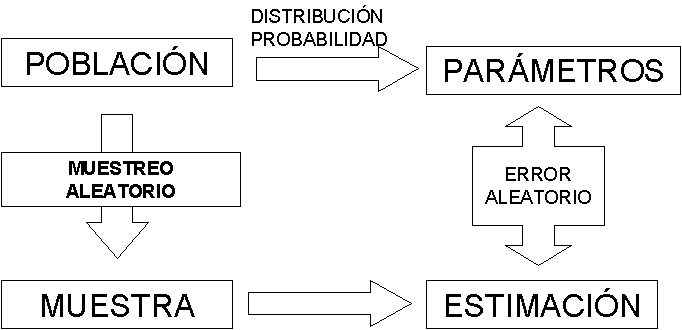
Dado que este es un módulo de diseño, únicamente mencionaremos algunas cosas importantes a la hora de efectuar el diseño. En los siguientes gráficos se presentan aquellos problemas que resuelve la estadística, así como un esquema de análisis de estos datos. Para mayor profundidad y compresión debería consultarse algún manual de estadística, asistir a un curso o consultar con un profesional.

Primero hay que diferenciar que tipo de variable se va a estudiar. Si se trata de variables cuantitativas o cualitativas, dado que la medida y el parámetro a estimar son distintos. En el caso de variables cualitativas, hablaremos de porcentajes, con lo cual el tamaño muestral y el tipo de análisis será para porcentajes. En el caso de variables continuas hablaremos de medias o de percentiles. Además del tipo de variables habrá que tener en cuenta el modo de recogerlas, los esquemas de codificación a utilizar etc. 

Como ya comentamos el tipo de variables a incluir también hay que tenerlo en cuenta, se deben de elegir no solo la variable respuesta o de interés, sino aquellas que se consideren relacionadas con ellas, bien porque son las que se consideran que si un sujeto esta expuestos a ellas tendrá la enfermedad, bien porque pueden estar encubriendo falsas relaciones entre la exposición y el problema a estudio.

En cuanto a la estrategia de análisis se debe de seguir tres pasos:

1) Análisis descriptivo.

Es la fase más importante del análisis en el por medio de tablas y gráficos se debe de resumir la información recogida en las muestras, permite generar nuevas hipótesis no planteadas, así como conocer a los sujetos de estudio. Además de las tablas y gráficos, se debe de calcular estimaciones puntuales y por intervalos de los parámetros seleccionados, habitualmente porcentajes para variables cualitativas y medias para variables cuantitativas. El intervalo de confianza permite medir el error y indicar que con una determinada probabilidad (95%) el porcentaje o medio para la población a estudio se encuentra entre los dos valores del intervalo.

A partir de la matriz de datos, podemos obtener para describir una variable medidas de:

2) Análisis simple de relación

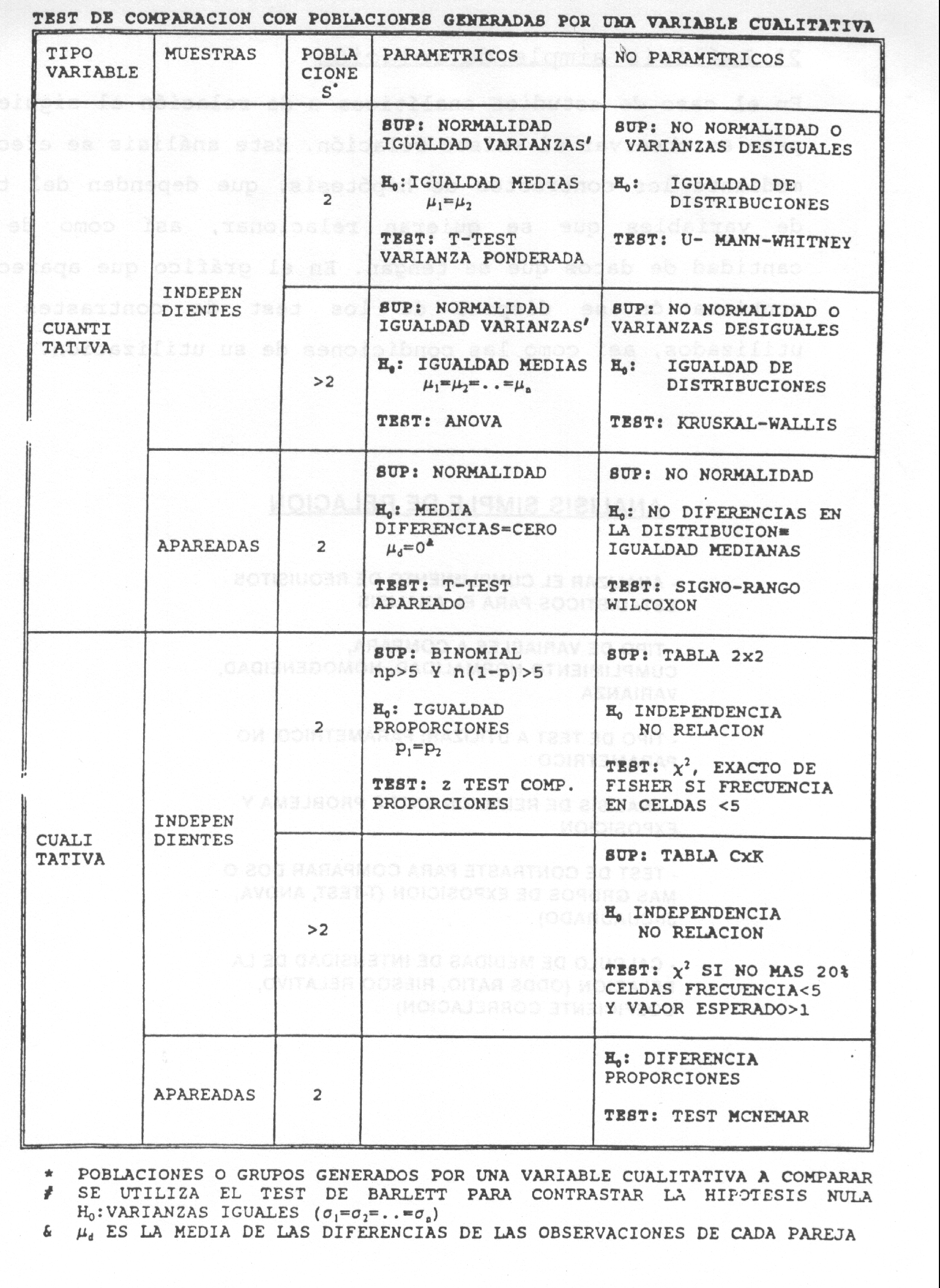
En el caso de estudios analíticos o de relación el siguiente paso es observar si existe relación. Este análisis se efectúa mediante los contrastes de hipótesis, que dependen del tipo de variables que se quieran relacionar, así como de la cantidad de datos que se tengan.  En el gráfico que aparece a continuación se dispone de los test de contrastes mas utilizados así como las condiciones de su utilización.

En la tabla que aparece a continuación se exponen los tests de comparación con poblaciones generadas por una variable cualitativa.

3) Análisis múltiple de relación

Cuando se sospecha que la relación puede estar alterada por una tercera variable, por ejemplo sexo, se procede a estratificar la muestra para ver si la relación se mantiene en todos los grupos, es decir en cada sexo.

Cuando no únicamente se cree que la relación es entre tres variables sino que se pretende construir modelos de multirelación entre variables se utilizan diversos modelos de regresión.