Sesión 1: Análisis Espectral (I)

Introducción a la Serie de Fourier y Síntesis de Señales.

1. El Concepto Fundamental

Jean-Baptiste Joseph Fourier postuló que cualquier señal periódica puede representarse como una suma infinita de funciones sinusoidales de diferentes frecuencias y amplitudes (Armónicos).

Idea clave: Una señal compleja no es más que una suma de "ingredientes" senoidales.

2. Representación Matemática

f(t) = a_0 + \sum_{n=1}^{\infty} \left[ a_n \cos(n\omega_0 t) + b_n \sin(n\omega_0 t) \right]

Los coeficientes \(a_n\) y \(b_n\) definen la amplitud de cada componente espectral.

3. Series de Fourier de Señales Comunes

Onda Cuadrada

Armónicos impares. Caída \(1/n\).

\[f(t) = \frac{4}{\pi} \sum_{n=1,3,5...} \frac{1}{n} \sin(n\omega_0 t)\]

Diente de Sierra

Todos los armónicos. Caída \(1/n\).

\[f(t) = \frac{2}{\pi} \sum_{n=1} \frac{(-1)^{n+1}}{n} \sin(n\omega_0 t)\]

Sintetizador Espectral (Dominio del Tiempo)

Aumenta el número de armónicos para ver cómo se forma la señal.

Señal Objetivo

Armónicos (N): 1

4. Teorema de Parseval y Potencia (Onda Cuadrada)

Calculamos la potencia de una onda cuadrada de amplitud 1V desglosando cada uno de sus armónicos de forma trigonométrica mediante estos tres pasos:

1. Tensión de Pico: Se obtiene de la serie de Fourier (\(V_{pn} = \frac{4}{\pi n}\)). 2. Tensión Eficaz: Al ser una senoidal, \(V_{rms,n} = \frac{V_{pn}}{\sqrt{2}}\). 3. Potencia del Armónico: Se calcula como el cuadrado del valor eficaz: \(P_n = (V_{rms,n})^2 = \frac{V_{pn}^2}{2}\).

Armónico	V. Pico (\(b_n\))	V. Eficaz (RMS)	Potencia (\(P_n\))
n=1 (Fund.)	1.2732 V	0.9003 V	0.8106 W
n=3	0.4244 V	0.3001 V	0.0901 W
n=5	0.2546 V	0.1801 V	0.0324 W
SUMA PARCIAL (n=1 a 5):			0.9331 W
Diferencia (n > 5):			0.0669 W
POTENCIA TOTAL IDEAL:			1.0000 W

💡 Nota: Para alcanzar el 1.0000 W exacto, se deberían sumar infinitos armónicos.

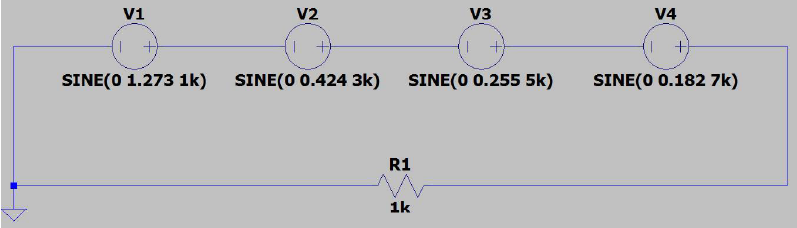
5. Implementación en LTspice

Conexión de generadores en serie para simular la serie de Fourier:

6. El Dominio de la Frecuencia (Espectro)

El dominio de la frecuencia nos permite ver la amplitud de cada ingrediente (armónico) por separado. Se representa mediante un diagrama de líneas donde el eje X es la frecuencia y el eje Y es la amplitud.

¿Por qué es importante? Muchas veces los problemas de comunicación (interferencias, ruido, distorsión) son invisibles en el tiempo pero saltan a la vista en la frecuencia.

Representación Espectral (Dominio de la Frecuencia)

Detalle de los primeros armónicos para identificar la composición de cada señal.

Visualizar Espectro de:

7. Filtrado Paso Bajo RC

Un filtro paso bajo es un circuito electrónico que permite el paso de frecuencias bajas pero atenúa (debilita) las frecuencias altas. El modelo más sencillo es el Filtro RC, compuesto por una resistencia (R) y un condensador (C).

Frecuencia de Corte (\(f_c\)): Es el punto donde la potencia se reduce a la mitad (-3dB). \[f_c = \frac{1}{2\pi R C}\]

En el dominio de la frecuencia, el filtro multiplica cada armónico por un factor de atenuación:

H(f) = \frac{1}{\sqrt{1 + (f/f_c)^2}}

Cuanto mayor sea la frecuencia del armónico (\(f\)) respecto a la frecuencia de corte (\(f_c\)), más desaparecerá esa componente del espectro de salida.

Simulación de Filtrado (Entrada vs Salida)

Ajusta la frecuencia de corte para ver cómo desaparecen los armónicos superiores.

ESPECTRO DE ENTRADA

ESPECTRO FILTRADO (SALIDA)

Frecuencia de Corte (\(f_c\)): 5

Filtrado Leve (fc alta) Filtrado Fuerte (fc baja)

Señal de Prueba: