Playing with hashing
Table of Contents
Keywords: hashing consistent hashing
Introduction
The goal is to define a hash function that allows the distribution of objects (data, files, web pages, etc.) in a fixed number of destinations (memory positions, disks, caches, etc.) in such a way that when we already have objects distributed in those destinations, the computational cost of adding new storage destinations is low.
The first step is to map an object \(o\) to \(\mathbb{N}\): \[ f(o) \longrightarrow n, \; n \in \mathbb{N}\]
Next we need to obtain a number from 1 to the number of destinations (\(N\)): \[h(n) \longrightarrow \{1,...,N\}\]
I will assume that the objects are Strings.
We will use the following funtion \(f\) to map Strings to integers:
\[f(o) = \textrm{decimal}(\textrm{getBits}(\textrm{sha256}(o)),16)\]
where getBits(s,b) return b bits of the first argument.
We will try with two different functions \(h\) and we will check how many objects (already stored) must be moved when we add 2 more destinations.
Non consistent hash function
The first hash function is: \[h(n) = \textrm{mod}(n,N) \]
We are going to obtain the destination (assuming we have \(N=20\)) of 1000 objects. Then we will add two more destinations and recalculate the destination of all the objects (changing the value of \(N\) from 20 to 22). Finally, we will obtain the percentage of objects that should be moved.
This is the Octave code:
% Number of objects D=1000; x=cell(D,1); % Let's generate objects for i=1:D x{i}=['/jgutierrez/masterTWCAM/videos/video_promocion',num2str(i),'.mp4']; endfor % Assume we have 20 destinations N=20; dest=zeros(D,1); for i=1:D % Obtain a number for each object f = hex2dec(substr(hash('sha256',x{i}),1,4)); % Apply function to get a number from {0,19} to get destination of object dest(i)=mod(f,N); endfor % Assume we add 2 destinations N=22; dest_2=zeros(D,1); for i=1:D % Obtain a number for each object f = hex2dec(substr(hash('sha256',x{i}),1,4)); % Apply the same function to get a number from {0,21} dest_2(i)=mod(f,N); endfor %Distribution of objects in destinations: dist=zeros(N,1); for i=1:N dist(i)=sum(dest_2==i); endfor bar([1:N],dist) % Check how many objects must be moved diff=dest-dest_2; nobjs=sum(abs(diff)>0); disp('Percentage objects that should be moved: ') 100*(nobjs/D)
Percentage objects that should be moved: ans = 91.400
The following figure shows the number of objects per destination:
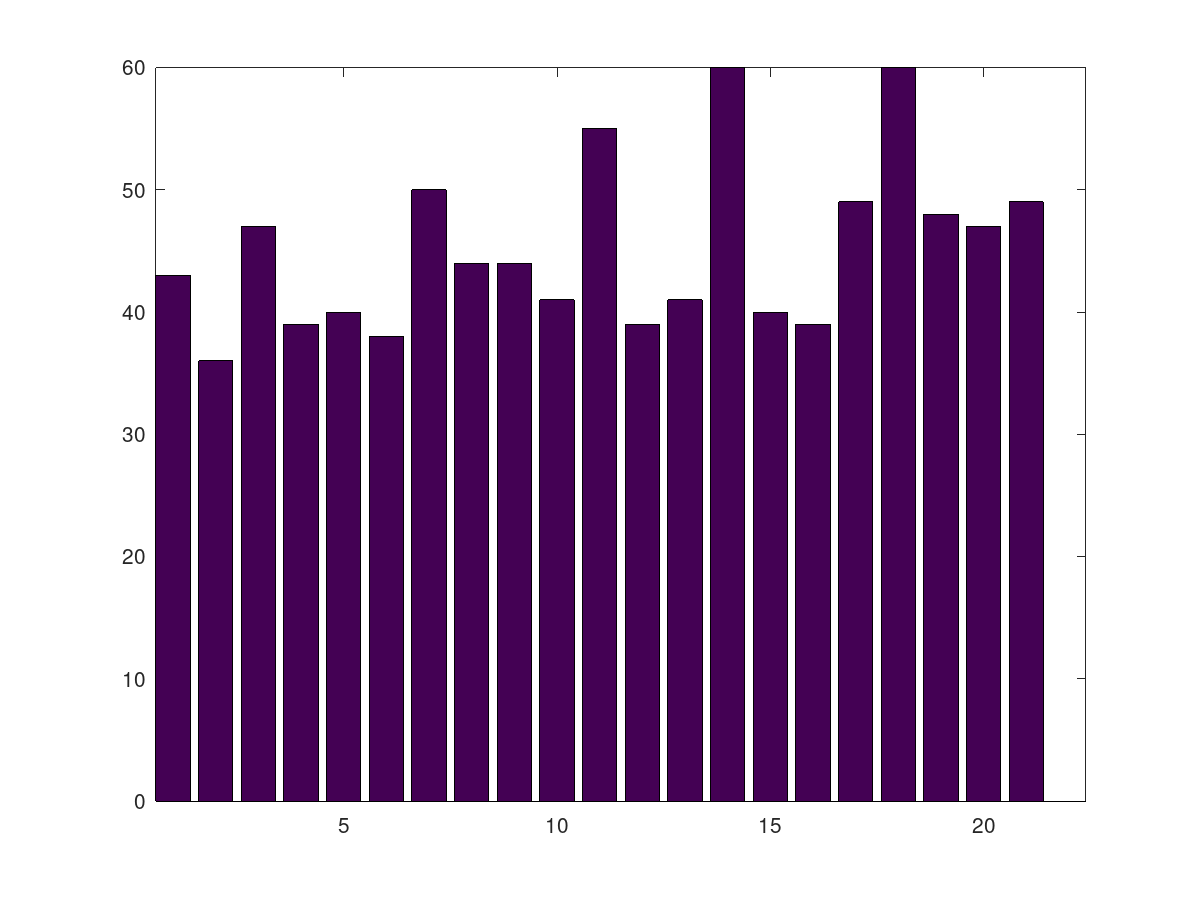
More consistent hash function
In this case we are going to distribute integers between \([0,2^{16}]\) and store those numbers (I will call these numbers "the ring" as it is the name that is used in swift):
N=20; ring=zeros(1,N); for i=1:N ring(i) = hex2dec(substr(hash('sha256',['destino' num2str(i)]),1,4)); end ring
ring =
Columns 1 through 10:
48602 22285 36368 3063 8548 24962 42288 20200 26066 62521
Columns 11 through 20:
5594 26554 11579 24774 28534 55909 18327 42345 54518 49062
To obtain the destination of an object apply the following function (given the integer for this object, obtain the position of the nearest ring number):
diff=abs(ring-n); vmin=min(diff); pos=find(diff==vmin);
This is the final code (we only change the \(h\) function):
% Number of objects D=1000; x=cell(D,1); for i=1:D x{i}=['/jgutierrez/masterTWCAM/videos/video_promocion',num2str(i),'.mp4']; endfor % Assume we have 20 destination to put those objects % Build the ring: N=20; ring=zeros(N,1); for i=1:N ring(i) = hex2dec(substr(hash('sha256',['destino' num2str(i)]),1,4)); end % Obtain the destination of each object dest=zeros(D,1); for i=1:D % Obtain a number from the object f = hex2dec(substr(hash('sha256',x{i}),1,4)); % Check the position of the nearest number in the ring diff=abs(ring-f); vmin=min(diff); pos=find(diff==vmin); dest(i)=pos; endfor % We add 2 more destinations % Rebuild ring N=22; ring2=zeros(N,1); for i=1:N ring2(i) = hex2dec(substr(hash('sha256',['destino' num2str(i)]),1,4)); end % Obtain the destination of each object dest_2=zeros(D,1); for i=1:D % Obtain a number from the object f = hex2dec(substr(hash('sha256',x{i}),1,4)); % Check the position of the nearest number in the ring diff=abs(ring2-f); vmin=min(diff); pos=find(diff==vmin); dest_2(i)=pos; endfor %Distribution of objects in destinations: dist=zeros(N,1); for i=1:N dist(i)=sum(dest_2==i); endfor bar([1:N],dist) % Check how many objects must be moved diff=dest-dest_2; nobjs=sum(abs(diff)>0); disp('Percentage objects that should be moved: ') 100*(nobjs/D)
Percentage objects that should be moved: ans = 6.4000
The following figure shows the number of objects per destination:
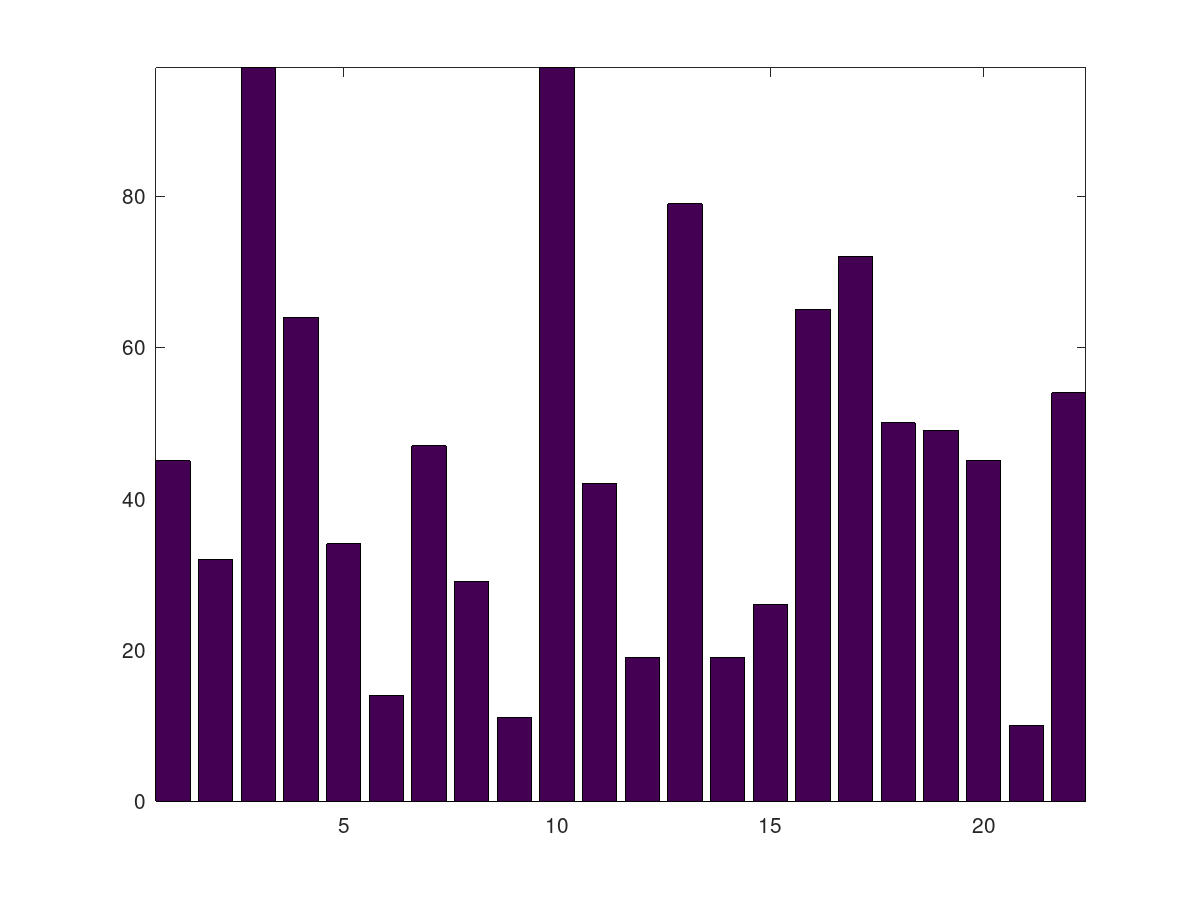
We see that in this case, we need to move 6.4% of the objects while in the first case 91.4% of the objects needed to be relocated.
If you have a lot of objects already stored in a distributed system this is a significant saving, and can reduce system downtime.