TEMA 1. CONCEPTOS de CRISTALOGRAFÍA.

1.2. Redes 2D.

Para familiarizarnos con los conceptos de cristalografía es útil comenzar usando modelos bidimensionales, más fáciles de visualizar que los tridimensionales que son los característicos de los sólidos. Una analogía útil es un papel impreso de decoración, en el que, de manera regular y en las dos dimensiones, se repite una imagen que llamamos motivo.

Podemos ver en este modelo como el motivo se repite de manera regular en el espacio bidimensional de acuerdo con una secuencia de traslaciones. Se definen "puntos equivalentes" aquellos que tienen el mismo entorno. Hay infinitos grupos de puntos equivalentes.

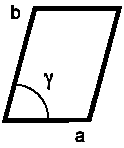
La celda en 2D es un paralelogramo que, por simple traslación en la dirección de los ejes, genera todo el retículo bidimensional. Viene descrita por las dimensiones de los ejes a , b y el ángulo γ que forman ambos ejes.

No hay una celda única. En la figura derecha vemos diferentes celdas seleccionadas. Todas ellas cumplen la condición de generar el modelo o retículo pero no todas tienen el mismo tamaño.

Hay celdas que contienen solo un motivo, como las 1,2,3,6,7 y 8, y otras que contienen dos 4 y 5. Se cuentan los motivos situados dentro de la celda con factor 1, los situados en aristas con factor 0.5 y los situados en vértices con factor 0.25. Las celdas de menor tamaño, que contienen un único motivo se denominan celdas primitivas.Las celdas 1,2,3,6 y 7 se diferencian tan solo en el origen.

Se elige como celda unidad, entre las celdas primitivas la de mayor simetría. En este caso, las celdas 1 y 3 en la figura.

Los vértices de la celda se denominan puntos reticulares. Se caracterizan por tener todos el mismo entorno dentro del retículo y ser puntos infinitesimales a diferencia de los átomos que tienen dimensiones finitas. Es de destacar que los puntos reticulares no siempre coinciden con los átomos del motivo, como ocurre por ejemplo en las celdas 3,5,6 y 7. El conjunto de puntos reticulares constituye el retículo cristalino.

Bibliografía

Al Indice