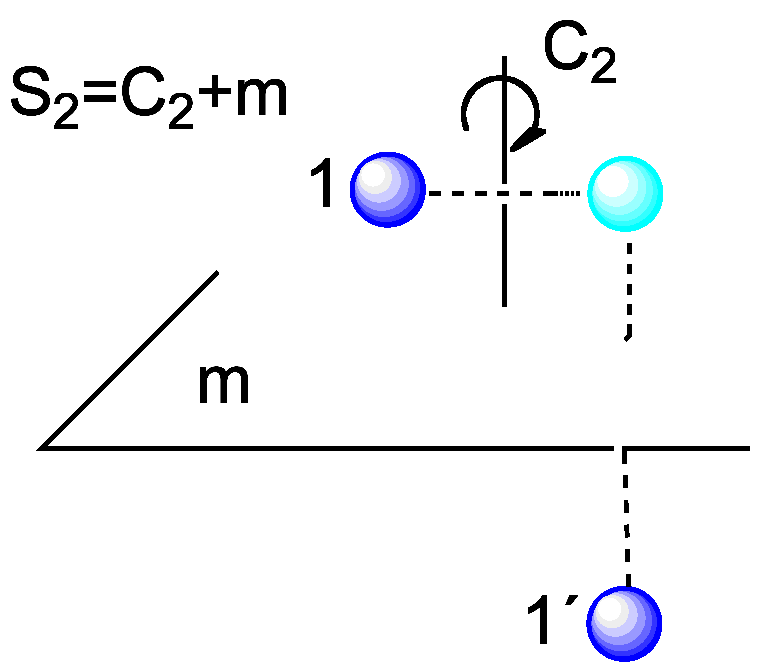Conceptos de Cristalografía.
Tema 1. Conceptos de cristalografía.
1.6. Simetría del cristal.
Al Indice


Hemos visto que para conocer la estructura de un sólido cristalino necesitamos los datos de la celda unidad y las posiciones de los átomos/iones dentro de la celda. En el caso del grafito se necesitaron cuatro coordenadas para localizar todos los átomos. En muchos casos la simetría dentro de la celda repite los átomos y el número de coordenadas necesarias se reduce.
Combinando las 14 redes de Bravais con las operaciones de simetría, resultan 230 formas diferentes de relacionar unos átomos con otros dentro del cristal. Se denominan Grupos espaciales.
El centro de inversión situado en el centro de la celda o en el origen de coordenadas, implica implica una transformación de las coordenadas de X,Y,Z a -X,-Y,-Z.
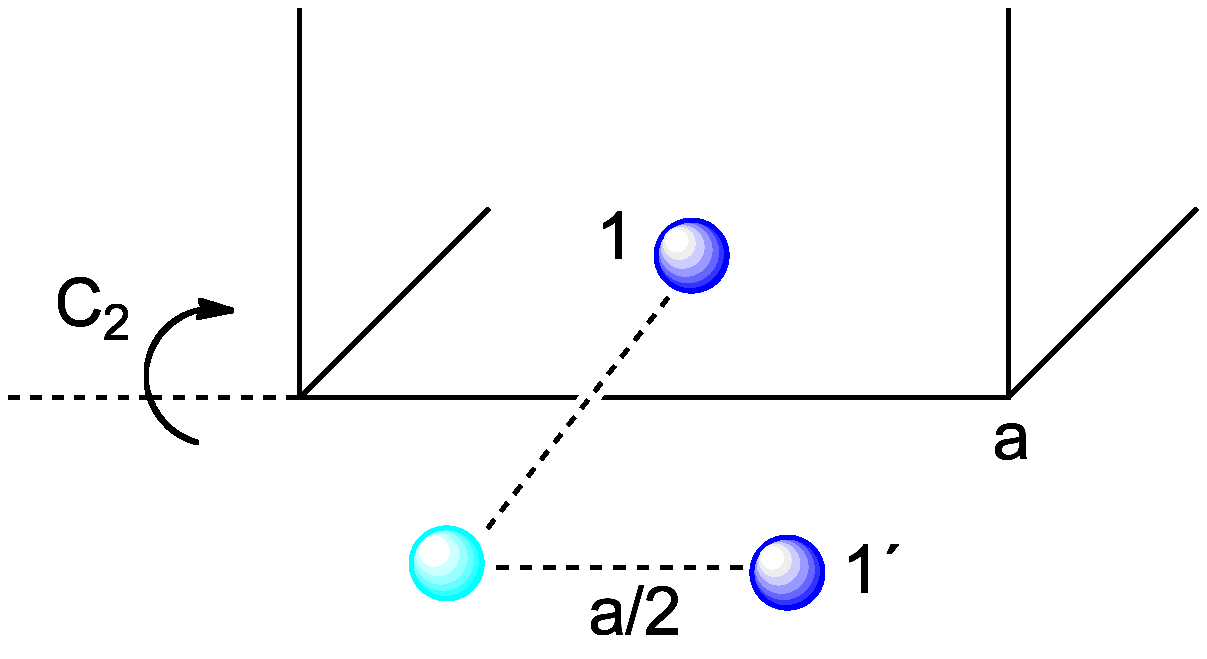
En los cristales, los ejes de simetría sólo pueden ser binarios (2), ternarios (3), cuaternarios (4) ó senarios (6). Los números entre paréntesis es el orden de la rotación, n. Cada eje produce saltos de 360/n grados.
Una rotación por un eje de rotación de orden 2, C2, en la dirección del eje Y, produce este cambio de
coordenadas X,Y,Z ==> -X,Y,-Z. Observad que las coordenadas -X o 1-X son idénticas de manera que la
rotación C2 para un átomo de coordenadas (0.2,0.6,0.3) se puede escribir indistintamente como
(-0.2,0.6,-0.3) ó (0.8,0.6,0.7).
Una rotación por un eje C4, en la dirección del eje Z, produce los siguientes cambios de coordenadas:
(X,Y,Z)(Y,-X,Z)(-X,-Y,Z)(-Y,X,Z).
Los cambios de coordenadas para rotaciones de orden 3 o 6 son más complejas.
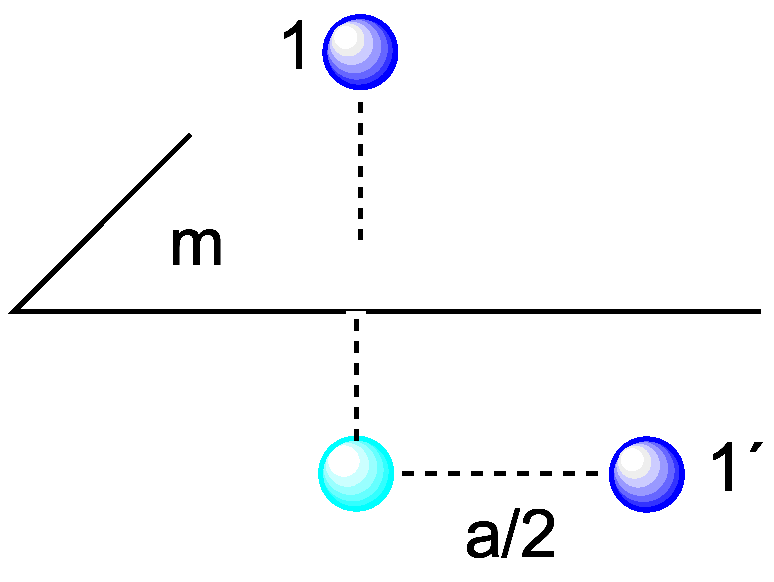
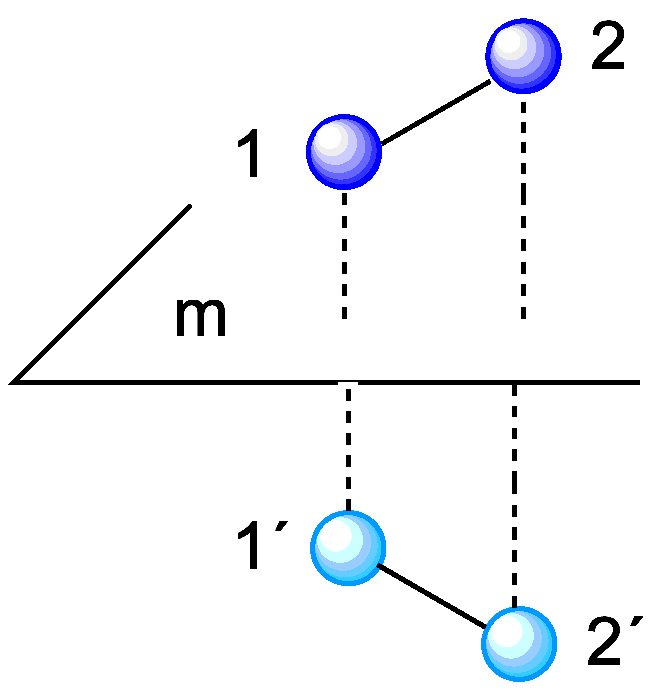
Un plano de simetría, representado por la letra "m", supone el siguiente cambio de coordenadas:
(X,Y1,Z)==> (X,Y2,Z) donde el promedio de las coordenadas Y1 e Y2
es la del plano de simetría.
Una rotación impropia, Sx, es una rotación de orden x acompañada de una
reflexión respecto de un plano perpendicular al eje de rotación. Si el eje de rotación es el Y, se
producirá el siguiente cambio de coordenadas:
(X,Y1,Z)==> (-X,Y2,-Z), donde el promedio de las coordenadas Y1 e Y2
es la del plano de simetría.
/p>
 |
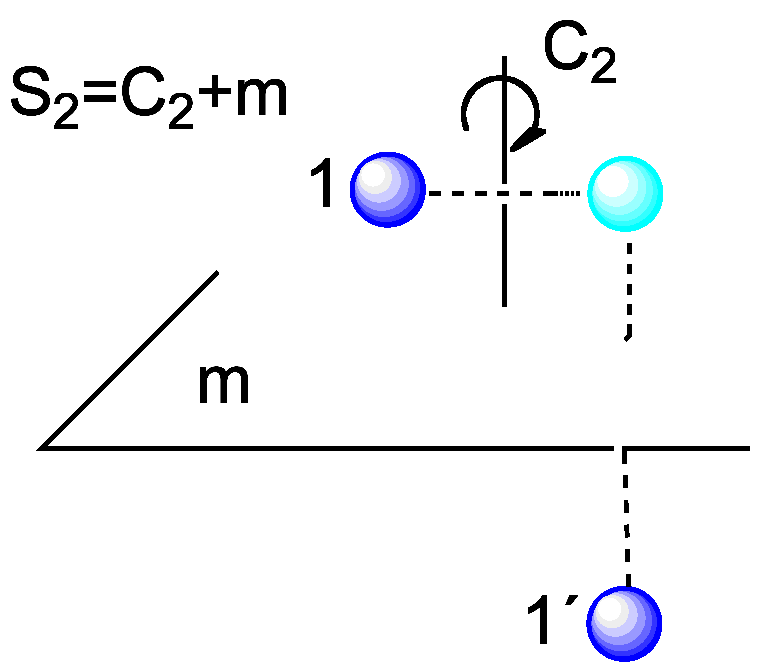 |
Quedan dos operaciones características de la simetría cristalina. A diferencia de las anteriores,
cuando se aplican no queda ningún punto invariante. Se denominan operaciones de simetría espacial.
Los ejes helicoidales son una rotación acompañada de una traslación en la dirección
del eje de rotación. El cambio de coordenadas que se produce es:
(X,Y,Z)==> (-X,Y+0.5,-Z).
Los planos de deslizamiento se representan por las letras a, b, c, n ó d, dependiendo
de que la traslación asociada a la reflexión sea paralela a las traslaciones reticulares (a, b, c) o
a una diagonal de un plano reticular (n) ó a una diagonal de la celdilla elemental (d).
Para más información sobre operaciones de simetría, visitar:
Página Web
 |
Al Indice