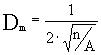
|
|
|
|
E
STADÍSTICO DEL VECINO MÁS PRÓXIMO. LEY DE CLARK-EVANS
Se considera de interés conocer de modo cuantitativo y preciso como es la disposición espacial de los diversos puntos del espacio que representan los centros de los municipios del Área Metropolitana de Valencia. Los centros de los 60 municipios del área ( se ha eliminado los tres de menos de 1000 habitantes) no se refieren a su centro de gravedad , se han tomado como centros los lugares relevantes de cada municipio, bien por encontrase su centro histórico , de comunicaciones , ayuntamiento o algún lugar emblemático .
La disposición espacial observada de los centros municipales debe compararse con las tres teórica y normalmente planteadas. ( Racionero , L. 1985) Es decir :
■ Aletaroria . Cualquier localización del plano tiene la misma probabilidad de recibir uno de los puntos o centros. No afectando la existencia de un punto dado a la localización de otro.
■ Regular . En esta disposición , por el contrario, los puntos están situados de manera que cubren todas las localizaciones del área de forma exhaustiva , formando una malla regular . La distancia que separa los puntos tiende a ser similar. Es la forma hexagonal habitual planteada por Christaller
■ Concentrada . La disposición concentrada supone la existencia de puntos-centros que se encuentran agrupados en uno varios pequeños espacios del área . Existiendo porciones amplias del terreno en las que no se ubica ningún punto.
La disposición real de los puntos o centros no suele coincidir nunca con ninguna de las tres teóricamente establecidas. Si bien existirán ciertas semejanzas con alguna de ellas , semejanzas cuantificables mediante el denominado "estadístico del vecino más próximo"
Dicho estadístico se formula de la siguiente manera .
(expresión
tomada de Bosque ,J.(1992))
Siendo
n = al número de puntos o centros , en nuestro caso 60
A = el área total , medida en las mismas unidades ( pero superficiales) que las distancias entre puntos ; en nuestro caso 1215 kilómetros cuadrados
D0 = distancia media de las mínimas distancias entre puntos o centros de los municipios tomadas en kilómetros
Tendremos que la distancia media
teórica es 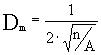
Siendo el valor del estadístico vecino más próximo .
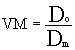
su valor oscila entre 0 y 2,15 .
Dicha expresión es transformada de la propuesta por Clark-Evans . Cuya formulación es:
ρ = densidad de puntos por superficie = n/A = número de puntos/ superficie
d = distancia media observada = media de las mínimas distancias observadas entre puntos
índice de Clark-Evans
=
![]() siendo
sus valores extremos 0 y 2,15
siendo
sus valores extremos 0 y 2,15
En ambos casos
Si el resultado fuera 0 la distribución de puntos sería lógicamente concentrada, si el valor del estadístico fuese 1 , las dos distancias , observada y teórica serían iguales por lo que estaríamos ante una distribución de los centros aleatoria . Si el estadístico se acerca a su valor máximo (2,15) ,estaríamos ante una distribución regular.
En el caso que nos ocupa la Dm
vendría dada por
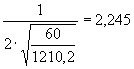 km.
km.
60 son los centros de los municipios.
1210,2 son los km2 que supone el área , 1215 menos los 4,83 que suponen los municipios de Fortaleny , Lugar Nuevo y Emperador de los que se prescinde.
La distancia media teórica sería Dm = 2,245
La distancia media observada Do se ha calculado en 1985 metros (distancias mínimas entre municipios)
Estructura del vecino más próximo
Por lo que el valor del estadístico
![]()
se puede comprobar
que también el valor del Ice = 0,884.
Ante estos resultados podemos hablar , por tanto
, de disposición
aleatoria de los centros municipales con cierta tendencia a la concentración
espacial .
Para concretar la cuestión se lleva a cabo un contraste de hipótesis en el sentido de verificar si es posible que la media de las distancias fuera 2245 , con lo que tendríamos un VM = 1 y por tanto una disposición aleatoria de los centros de los municipios.( ir a programa de realización del contraste)
Realizado el contraste para un nivel de significación de 0,05 . Conociendo que la desviación típica de las distancias mínimas entre centros de municipios se ha calculado en 1443,68. Se llega a la conclusión de que no podemos rechazar la hipótesis de que la distancia media observada sea 2245 , por lo que consideramos que la distribución de los centros de los municipios es aleatoria en el espacio del área metropolitana .

