Práctica 2
IMLE
Para realizar la práctica primero deben generarse tres variables por simulación. Para ello, primero fijamos la semilla para la aleatorización: set.seed(444) cada alumno debe sustituir 444 por su correspondiente número despues seguimos las instucciones que se detallan
set.seed(444)
1.-Considerar v1,v2,v3 como tres variables estadísticas de una cierta base de datos constituida por 250 individuos.Añadir a la base de datos una variable de identificación numérica que recorra los numerales del 1 al 250. Construir un dataframe yuxtaponiendo( función cbind) las tres variables y el identificador ( cuatro variables) Le otorgamos un nombre ( asignamos un objeto) a la base de datos y la analizamos descriptivamente.
Obtener al menos media, varianza, desviación típica, mediana, moda y cuartiles para todas las variables ( para la variable id no ). Obener el histograma . Se aconseja inspirarse en las funciones “descriptiva” y “adescriptivo” del archivo https://www.uv.es/mlejarza/azar/sim.htm (usadas tal cual no serán suficientes)
Nota conceptual : v1,v2 y v3 se generan a partir de distribuciiones de probabilidad pero (una vez generadas) SON variables estadísticas ( con sus respectivas distribuciones de frecuencias) ir a punto siguiente
v1<-rpois(250,lambda=7)#250 datos obtenidos al azar según una distribución de Poisson de parámetro lambda=7#250 datos obtenidos al azar según una distribución Biomial de parámetros n= 12 y p=0.6
v2<-rnorm(250,8,2.8) #250 datos obtenidos al azar según una distribución Normal de media 8 y desv.típica 2.8
v3<-rbinom(250,12,0.6)
id<-1:250bdatos<-as.data.frame(cbind(id,v1,v2,v3))
summary(bdatos)
## id v1 v2 v3
## Min. : 1.00 Min. : 2.000 Min. :-1.990 Min. : 3.000
## 1st Qu.: 63.25 1st Qu.: 5.000 1st Qu.: 6.185 1st Qu.: 6.000
## Median :125.50 Median : 7.000 Median : 8.150 Median : 7.000
## Mean :125.50 Mean : 6.944 Mean : 8.136 Mean : 7.188
## 3rd Qu.:187.75 3rd Qu.: 8.000 3rd Qu.:10.078 3rd Qu.: 8.000
## Max. :250.00 Max. :14.000 Max. :16.905 Max. :11.000## media varianza coef.var
## [1,] 6.944000 5.940864 0.3510064
## [2,] 8.135531 8.559681 0.3596192
## [3,] 7.188000 2.480656 0.2191166_____________________________________________
2.- Construir las tablas de frecuencia ( frecuencias relativas) de las tres variables v1,v2 y v3 . Representar gráficamente las distribuciones
Comentar qué ocurre en el caso de la segunda de las variables, ¿por qué ocurre ?. (Pista: la distribución normal es una distrib. de variable aleatoria continua )
A partir de ellas, después, en el punto 3, construiremos tres variables aleatorias discretas. (Se recomienda, de nuevo consultar el archivo de antes)
ir a punto anterior ir a punto siguiente
## v1
## 2 3 4 5 6 7 8 9 10 11 12 13 14
## 3 9 25 39 46 39 27 20 18 12 6 5 1## v2
## -1.9899887564021 0.160303461162536 0.631313728798288 1.79779465134775
## 1 1 1 1
## 1.90175117623849 2.20775131611033 2.3605366588653 2.39697967304565
## 1 1 1 1
## 2.40061472414512 2.98627560288393 2.99822279621424 3.11921698375362
## 1 1 1 1
## 3.32247886768862 3.32257593076167 3.38876686786049 3.53487333311754
## 1 1 1 1
## 3.85623415142906 4.03609149893955 4.06081889090651 4.11151906982154
## 1 1 1 1
## 4.31344633603439 4.40673325097952 4.46759004501553 4.52110835578764
## 1 1 1 1
## 4.56760717912453 4.56851313430965 4.63603150437771 4.64165676939131
## 1 1 1 1
## 4.71793940245555 4.75918003554902 4.80112925502462 4.93420823337101
## 1 1 1 1
## 5.03784227111326 5.04071273799435 5.13017315155555 5.17393555293854
## 1 1 1 1
## 5.17532039968892 5.19371694586671 5.24749000660756 5.25401728225444
## 1 1 1 1
## 5.39280726579772 5.39580909333139 5.56623043875069 5.60649995479985
## 1 1 1 1
## 5.62194849917454 5.62868494177586 5.66224513397236 5.70188879388203
## 1 1 1 1
## 5.70655758195858 5.7127880662201 5.75500333359522 5.79726422832296
## 1 1 1 1
## 5.82996941569435 5.85623937189902 5.85779649966818 5.86088913962101
## 1 1 1 1
## 5.89485301386109 5.90674687318464 5.92092874520855 5.93542694898489
## 1 1 1 1
## 5.95396137831027 5.99629499691885 6.17567453173424 6.21475377430736
## 1 1 1 1
## 6.23079104016239 6.24140086164753 6.26688942933431 6.30488947421798
## 1 1 1 1
## 6.39941654812276 6.43003573406889 6.4873855011815 6.49493092182029
## 1 1 1 1
## 6.51927411084647 6.57228068183414 6.61005004688062 6.78261125065176
## 1 1 1 1
## 6.80814458185725 6.84160740804475 6.85968593382816 6.90827345189321
## 1 1 1 1
## 6.91388446913737 6.92102350025721 6.92699706276499 6.98479951927431
## 1 1 1 1
## 6.98764159625012 7.00483490499026 7.05316618061229 7.07512186937241
## 1 1 1 1
## 7.07689698682969 7.1122984445105 7.15178349734023 7.17174760398428
## 1 1 1 1
## 7.33843855449715 7.36360386431442 7.38072134123871 7.38834615631528
## 1 1 1 1
## 7.40034301491553 7.43202842012206 7.43909697388573 7.47668160640205
## 1 1 1 1
## 7.48097295684571 7.56410587716868 7.56429158900258 7.5822653761871
## 1 1 1 1
## 7.60094637826755 7.60723219179878 7.61004880802453 7.62514865501
## 1 1 1 1
## 7.62709792273803 7.63423211186193 7.70510409973881 7.73670575333336
## 1 1 1 1
## 7.74499153658842 7.74984680524906 7.78104904019267 7.87247194847798
## 1 1 1 1
## 7.90927620842947 7.94575754152218 7.95171472560479 8.00585641707433
## 1 1 1 1
## 8.01932886759184 8.06656309519708 8.0752991315578 8.12190607913779
## 1 1 1 1
## 8.12345505680835 8.17746893724269 8.23088005043939 8.23833118878273
## 1 1 1 1
## 8.26580864772702 8.26773953999685 8.28355200211534 8.30140613575332
## 1 1 1 1
## 8.3255362470429 8.37033262428342 8.40827542807491 8.41039442864204
## 1 1 1 1
## 8.42775129741709 8.49981212967262 8.50722549376498 8.52047005845179
## 1 1 1 1
## 8.54493868394372 8.56643759866158 8.60143941225252 8.61635844401147
## 1 1 1 1
## 8.6201390378971 8.62463134040049 8.69857650085491 8.72552548366746
## 1 1 1 1
## 8.81160048199054 8.81166107266692 8.83794418411698 8.86883556559362
## 1 1 1 1
## 8.88126614140576 8.91003687665591 8.98543766404693 9.01904463008414
## 1 1 1 1
## 9.04030297142847 9.15684475120749 9.16107251288403 9.17216639195574
## 1 1 1 1
## 9.2143185988388 9.30513569631776 9.36090499657223 9.43238625463358
## 1 1 1 1
## 9.43626388711241 9.46398437578406 9.46665952065498 9.47056874248981
## 1 1 1 1
## 9.5007041971117 9.508581965519 9.53669662916864 9.54566246664581
## 1 1 1 1
## 9.63166891209124 9.64315709557938 9.65165824489433 9.66304769758272
## 1 1 1 1
## 9.70376866645605 9.7196719054091 9.79645371508232 9.79963192510712
## 1 1 1 1
## 9.88395915059212 9.94504296753683 9.98356722172012 10.016310303259
## 1 1 1 1
## 10.0221616958398 10.0261446381799 10.066922941646 10.0812369326834
## 1 1 1 1
## 10.0943954207186 10.1139219153613 10.1554107116085 10.1806647312592
## 1 1 1 1
## 10.2250631641628 10.2365353409898 10.3075671919595 10.3247663387915
## 1 1 1 1
## 10.3542776260516 10.3834390937908 10.3998834450793 10.4259822256322
## 1 1 1 1
## 10.4264425274663 10.4821622858051 10.5090328546378 10.5317972428092
## 1 1 1 1
## 10.5666189525113 10.7151589000925 10.7499280038621 10.8881659501671
## 1 1 1 1
## 10.9171461797526 10.9460283051783 10.9593997415422 11.074061867104
## 1 1 1 1
## 11.093988368276 11.1023241261801 11.1722211675596 11.2206922675539
## 1 1 1 1
## 11.2553689893331 11.3273918460755 11.4323150254305 11.4931405356772
## 1 1 1 1
## 11.5063739504155 11.5207519031208 11.8640026491383 11.9104083969926
## 1 1 1 1
## 11.9133455487755 12.0236740669371 12.0471106250444 12.0701642097287
## 1 1 1 1
## 12.0722045704752 12.139558690161 12.1720922144552 12.3472265398368
## 1 1 1 1
## 12.4031926135823 12.4562023468829 12.5611714576892 12.704615905003
## 1 1 1 1
## 12.7706541831852 12.8011481611077 12.9535742181507 12.9566944229351
## 1 1 1 1
## 13.125522611581 13.4759927508365 13.8235298872779 13.9212984264364
## 1 1 1 1
## 14.0238175071414 14.2833005108229 14.3431078341221 14.6704275375853
## 1 1 1 1
## 16.0794573925562 16.9046873000418
## 1 1## v3
## 3 4 5 6 7 8 9 10 11
## 3 6 27 46 66 46 41 11 4Tabla de frecuencias relativas de v1 ## v1
## 2 3 4 5 6 7 8 9 10 11 12 13
## 0.012 0.036 0.100 0.156 0.184 0.156 0.108 0.080 0.072 0.048 0.024 0.020
## 14
## 0.004Tabla de frecuencias relativas de v2 ## v2
## -1.9899887564021 0.160303461162536 0.631313728798288 1.79779465134775
## 0.004 0.004 0.004 0.004
## 1.90175117623849 2.20775131611033 2.3605366588653 2.39697967304565
## 0.004 0.004 0.004 0.004
## 2.40061472414512 2.98627560288393 2.99822279621424 3.11921698375362
## 0.004 0.004 0.004 0.004
## 3.32247886768862 3.32257593076167 3.38876686786049 3.53487333311754
## 0.004 0.004 0.004 0.004
## 3.85623415142906 4.03609149893955 4.06081889090651 4.11151906982154
## 0.004 0.004 0.004 0.004
## 4.31344633603439 4.40673325097952 4.46759004501553 4.52110835578764
## 0.004 0.004 0.004 0.004
## 4.56760717912453 4.56851313430965 4.63603150437771 4.64165676939131
## 0.004 0.004 0.004 0.004
## 4.71793940245555 4.75918003554902 4.80112925502462 4.93420823337101
## 0.004 0.004 0.004 0.004
## 5.03784227111326 5.04071273799435 5.13017315155555 5.17393555293854
## 0.004 0.004 0.004 0.004
## 5.17532039968892 5.19371694586671 5.24749000660756 5.25401728225444
## 0.004 0.004 0.004 0.004
## 5.39280726579772 5.39580909333139 5.56623043875069 5.60649995479985
## 0.004 0.004 0.004 0.004
## 5.62194849917454 5.62868494177586 5.66224513397236 5.70188879388203
## 0.004 0.004 0.004 0.004
## 5.70655758195858 5.7127880662201 5.75500333359522 5.79726422832296
## 0.004 0.004 0.004 0.004
## 5.82996941569435 5.85623937189902 5.85779649966818 5.86088913962101
## 0.004 0.004 0.004 0.004
## 5.89485301386109 5.90674687318464 5.92092874520855 5.93542694898489
## 0.004 0.004 0.004 0.004
## 5.95396137831027 5.99629499691885 6.17567453173424 6.21475377430736
## 0.004 0.004 0.004 0.004
## 6.23079104016239 6.24140086164753 6.26688942933431 6.30488947421798
## 0.004 0.004 0.004 0.004
## 6.39941654812276 6.43003573406889 6.4873855011815 6.49493092182029
## 0.004 0.004 0.004 0.004
## 6.51927411084647 6.57228068183414 6.61005004688062 6.78261125065176
## 0.004 0.004 0.004 0.004
## 6.80814458185725 6.84160740804475 6.85968593382816 6.90827345189321
## 0.004 0.004 0.004 0.004
## 6.91388446913737 6.92102350025721 6.92699706276499 6.98479951927431
## 0.004 0.004 0.004 0.004
## 6.98764159625012 7.00483490499026 7.05316618061229 7.07512186937241
## 0.004 0.004 0.004 0.004
## 7.07689698682969 7.1122984445105 7.15178349734023 7.17174760398428
## 0.004 0.004 0.004 0.004
## 7.33843855449715 7.36360386431442 7.38072134123871 7.38834615631528
## 0.004 0.004 0.004 0.004
## 7.40034301491553 7.43202842012206 7.43909697388573 7.47668160640205
## 0.004 0.004 0.004 0.004
## 7.48097295684571 7.56410587716868 7.56429158900258 7.5822653761871
## 0.004 0.004 0.004 0.004
## 7.60094637826755 7.60723219179878 7.61004880802453 7.62514865501
## 0.004 0.004 0.004 0.004
## 7.62709792273803 7.63423211186193 7.70510409973881 7.73670575333336
## 0.004 0.004 0.004 0.004
## 7.74499153658842 7.74984680524906 7.78104904019267 7.87247194847798
## 0.004 0.004 0.004 0.004
## 7.90927620842947 7.94575754152218 7.95171472560479 8.00585641707433
## 0.004 0.004 0.004 0.004
## 8.01932886759184 8.06656309519708 8.0752991315578 8.12190607913779
## 0.004 0.004 0.004 0.004
## 8.12345505680835 8.17746893724269 8.23088005043939 8.23833118878273
## 0.004 0.004 0.004 0.004
## 8.26580864772702 8.26773953999685 8.28355200211534 8.30140613575332
## 0.004 0.004 0.004 0.004
## 8.3255362470429 8.37033262428342 8.40827542807491 8.41039442864204
## 0.004 0.004 0.004 0.004
## 8.42775129741709 8.49981212967262 8.50722549376498 8.52047005845179
## 0.004 0.004 0.004 0.004
## 8.54493868394372 8.56643759866158 8.60143941225252 8.61635844401147
## 0.004 0.004 0.004 0.004
## 8.6201390378971 8.62463134040049 8.69857650085491 8.72552548366746
## 0.004 0.004 0.004 0.004
## 8.81160048199054 8.81166107266692 8.83794418411698 8.86883556559362
## 0.004 0.004 0.004 0.004
## 8.88126614140576 8.91003687665591 8.98543766404693 9.01904463008414
## 0.004 0.004 0.004 0.004 ## 9.04030297142847 9.15684475120749 9.16107251288403 9.17216639195574 ## 0.004 0.004 0.004 0.004 ## 9.2143185988388 9.30513569631776 9.36090499657223 9.43238625463358 ## 0.004 0.004 0.004 0.004 ## 9.43626388711241 9.46398437578406 9.46665952065498 9.47056874248981 ## 0.004 0.004 0.004 0.004 ## 9.5007041971117 9.508581965519 9.53669662916864 9.54566246664581 ## 0.004 0.004 0.004 0.004 ## 9.63166891209124 9.64315709557938 9.65165824489433 9.66304769758272 ## 0.004 0.004 0.004 0.004 ## 9.70376866645605 9.7196719054091 9.79645371508232 9.79963192510712 ## 0.004 0.004 0.004 0.004 ## 9.88395915059212 9.94504296753683 9.98356722172012 10.016310303259 ## 0.004 0.004 0.004 0.004 ## 10.0221616958398 10.0261446381799 10.066922941646 10.0812369326834 ## 0.004 0.004 0.004 0.004 ## 10.0943954207186 10.1139219153613 10.1554107116085 10.1806647312592 ## 0.004 0.004 0.004 0.004 ## 10.2250631641628 10.2365353409898 10.3075671919595 10.3247663387915 ## 0.004 0.004 0.004 0.004 ## 10.3542776260516 10.3834390937908 10.3998834450793 10.4259822256322 ## 0.004 0.004 0.004 0.004 ## 10.4264425274663 10.4821622858051 10.5090328546378 10.5317972428092 ## 0.004 0.004 0.004 0.004 ## 10.5666189525113 10.7151589000925 10.7499280038621 10.8881659501671 ## 0.004 0.004 0.004 0.004 ## 10.9171461797526 10.9460283051783 10.9593997415422 11.074061867104 ## 0.004 0.004 0.004 0.004 ## 11.093988368276 11.1023241261801 11.1722211675596 11.2206922675539 ## 0.004 0.004 0.004 0.004 ## 11.2553689893331 11.3273918460755 11.4323150254305 11.4931405356772 ## 0.004 0.004 0.004 0.004 ## 11.5063739504155 11.5207519031208 11.8640026491383 11.9104083969926 ## 0.004 0.004 0.004 0.004 ## 11.9133455487755 12.0236740669371 12.0471106250444 12.0701642097287 ## 0.004 0.004 0.004 0.004 ## 12.0722045704752 12.139558690161 12.1720922144552 12.3472265398368 ## 0.004 0.004 0.004 0.004 ## 12.4031926135823 12.4562023468829 12.5611714576892 12.704615905003 ## 0.004 0.004 0.004 0.004 ## 12.7706541831852 12.8011481611077 12.9535742181507 12.9566944229351 ## 0.004 0.004 0.004 0.004 ## 13.125522611581 13.4759927508365 13.8235298872779 13.9212984264364 ## 0.004 0.004 0.004 0.004 ## 14.0238175071414 14.2833005108229 14.3431078341221 14.6704275375853 ## 0.004 0.004 0.004 0.004 ## 16.0794573925562 16.9046873000418 ## 0.004 0.004Tabla de frecuencias relativas de v3 ## v3
## 3 4 5 6 7 8 9 10 11
## 0.012 0.024 0.108 0.184 0.264 0.184 0.164 0.044 0.016Diagramas de barras
__________________________________________________________________________________________
- Re-consideramos ( transformamos) las variables v1,v2, v3 como si fueran variables aleatorias (discretas). Para poder aplicar la función DiscreteDistribution(),antes habrá que hacer algunos arreglos. Representar gráficamente las tres distribuciones. Puede observarse que , de nuevo, la variable v2 tiene un comportamiento especial. Coméntalo. ¿cómo se puede llegar a representar un histograma para la variable v2 como el que aparece abajo? Si ejecutas la instrucción : plot(density(patatin)), en la que "patatin" es como hayas llamado al recorrido de la variable v2 te sale una aproximación continua a la distribución de la variable. ¿A qué se parece? .- Hay que hacerlo
Nota técnica: Interesará llamar a los 3 objetos de la clase "DiscreteDistribution" que obtengamos con un nombre diferenciado ( distinto de v1,v2 y v3 )
ir a punto anterior ir a punto siguiente
## $v1
## [1] "2" "3" "4" "5" "6" "7" "8" "9" "10" "11" "12" "13" "14"## $v2
## [1] "-1.9899887564021" "0.160303461162536" "0.631313728798288"
## [4] "1.79779465134775" "1.90175117623849" "2.20775131611033"
## [7] "2.3605366588653" "2.39697967304565" "2.40061472414512"
## [10] "2.98627560288393" "2.99822279621424" "3.11921698375362"
## [13] "3.32247886768862" "3.32257593076167" "3.38876686786049"
## [16] "3.53487333311754" "3.85623415142906" "4.03609149893955"
## [19] "4.06081889090651" "4.11151906982154" "4.31344633603439"
## [22] "4.40673325097952" "4.46759004501553" "4.52110835578764"
## [25] "4.56760717912453" "4.56851313430965" "4.63603150437771"
## [28] "4.64165676939131" "4.71793940245555" "4.75918003554902"
## [31] "4.80112925502462" "4.93420823337101" "5.03784227111326"
## [34] "5.04071273799435" "5.13017315155555" "5.17393555293854"
## [37] "5.17532039968892" "5.19371694586671" "5.24749000660756"
## [40] "5.25401728225444" "5.39280726579772" "5.39580909333139"
## [43] "5.56623043875069" "5.60649995479985" "5.62194849917454"
## [46] "5.62868494177586" "5.66224513397236" "5.70188879388203"
## [49] "5.70655758195858" "5.7127880662201" "5.75500333359522"
## [52] "5.79726422832296" "5.82996941569435" "5.85623937189902"
## [55] "5.85779649966818" "5.86088913962101" "5.89485301386109"
## [58] "5.90674687318464" "5.92092874520855" "5.93542694898489"
## [61] "5.95396137831027" "5.99629499691885" "6.17567453173424"
## [64] "6.21475377430736" "6.23079104016239" "6.24140086164753"
## [67] "6.26688942933431" "6.30488947421798" "6.39941654812276"
## [70] "6.43003573406889" "6.4873855011815" "6.49493092182029"
## [73] "6.51927411084647" "6.57228068183414" "6.61005004688062"
## [76] "6.78261125065176" "6.80814458185725" "6.84160740804475"
## [79] "6.85968593382816" "6.90827345189321" "6.91388446913737"
## [82] "6.92102350025721" "6.92699706276499" "6.98479951927431"
## [85] "6.98764159625012" "7.00483490499026" "7.05316618061229"
## [88] "7.07512186937241" "7.07689698682969" "7.1122984445105"
## [91] "7.15178349734023" "7.17174760398428" "7.33843855449715"
## [94] "7.36360386431442" "7.38072134123871" "7.38834615631528"
## [97] "7.40034301491553" "7.43202842012206" "7.43909697388573"
## [100] "7.47668160640205" "7.48097295684571" "7.56410587716868"
## [103] "7.56429158900258" "7.5822653761871" "7.60094637826755"
## [106] "7.60723219179878" "7.61004880802453" "7.62514865501"
## [109] "7.62709792273803" "7.63423211186193" "7.70510409973881"
## [112] "7.73670575333336" "7.74499153658842" "7.74984680524906"
## [115] "7.78104904019267" "7.87247194847798" "7.90927620842947"
## [118] "7.94575754152218" "7.95171472560479" "8.00585641707433"
## [121] "8.01932886759184" "8.06656309519708" "8.0752991315578"
## [124] "8.12190607913779" "8.12345505680835" "8.17746893724269"
## [127] "8.23088005043939" "8.23833118878273" "8.26580864772702"
## [130] "8.26773953999685" "8.28355200211534" "8.30140613575332"
## [133] "8.3255362470429" "8.37033262428342" "8.40827542807491"
## [136] "8.41039442864204" "8.42775129741709" "8.49981212967262"
## [139] "8.50722549376498" "8.52047005845179" "8.54493868394372"
## [142] "8.56643759866158" "8.60143941225252" "8.61635844401147"
## [145] "8.6201390378971" "8.62463134040049" "8.69857650085491"
## [148] "8.72552548366746" "8.81160048199054" "8.81166107266692"
## [151] "8.83794418411698" "8.86883556559362" "8.88126614140576"
## [154] "8.91003687665591" "8.98543766404693" "9.01904463008414"
## [157] "9.04030297142847" "9.15684475120749" "9.16107251288403"
## [160] "9.17216639195574" "9.2143185988388" "9.30513569631776"
## [163] "9.36090499657223" "9.43238625463358" "9.43626388711241"
## [166] "9.46398437578406" "9.46665952065498" "9.47056874248981"
## [169] "9.5007041971117" "9.508581965519" "9.53669662916864"
## [172] "9.54566246664581" "9.63166891209124" "9.64315709557938"
## [175] "9.65165824489433" "9.66304769758272" "9.70376866645605"
## [178] "9.7196719054091" "9.79645371508232" "9.79963192510712"
## [181] "9.88395915059212" "9.94504296753683" "9.98356722172012"
## [184] "10.016310303259" "10.0221616958398" "10.0261446381799"
## [187] "10.066922941646" "10.0812369326834" "10.0943954207186"
## [190] "10.1139219153613" "10.1554107116085" "10.1806647312592"
## [193] "10.2250631641628" "10.2365353409898" "10.3075671919595"
## [196] "10.3247663387915" "10.3542776260516" "10.3834390937908"
## [199] "10.3998834450793" "10.4259822256322" "10.4264425274663"
## [202] "10.4821622858051" "10.5090328546378" "10.5317972428092"
## [205] "10.5666189525113" "10.7151589000925" "10.7499280038621"
## [208] "10.8881659501671" "10.9171461797526" "10.9460283051783"
## [211] "10.9593997415422" "11.074061867104" "11.093988368276"
## [214] "11.1023241261801" "11.1722211675596" "11.2206922675539"
## [217] "11.2553689893331" "11.3273918460755" "11.4323150254305"
## [220] "11.4931405356772" "11.5063739504155" "11.5207519031208"
## [223] "11.8640026491383" "11.9104083969926" "11.9133455487755"
## [226] "12.0236740669371" "12.0471106250444" "12.0701642097287"
## [229] "12.0722045704752" "12.139558690161" "12.1720922144552"
## [232] "12.3472265398368" "12.4031926135823" "12.4562023468829"
## [235] "12.5611714576892" "12.704615905003" "12.7706541831852"
## [238] "12.8011481611077" "12.9535742181507" "12.9566944229351"
## [241] "13.125522611581" "13.4759927508365" "13.8235298872779"
## [244] "13.9212984264364" "14.0238175071414" "14.2833005108229"
## [247] "14.3431078341221" "14.6704275375853" "16.0794573925562"
## [250] "16.9046873000418"## $v3
## [1] "3" "4" "5" "6" "7" "8" "9" "10" "11"Las etiquetas de las tablas de frecuencia son de la clase list y hay que convertirlas en valores numericos.## [1] "list"
la instrucion unlist permite eliminar su caracter de lista, depués habrá que convertirla en número con as.integer
o as.doubleEn el caso de las de v2 interesa que sea double o numeric , más que integer
Después ya podremos convertir el par "recorrido , probabilidades ( frec.rel.)" en una distribución de probabilidad
para cada una de las tres variables.
Luego podremos representar las gráficas.
Histograma y densidad de la aproximación contínua de la variable v2. Debe realizarse, también.____________________________________________
4.Analizar las tres distribuciones obtenidas, calculando sus principales indicadores.
ir a punto anterior ir a punto siguiente
## esperanza mediana varianza coef.asimetría coef.curtosis
## 6.9440000 7.0000000 5.9408640 0.5192085 -0.1921383Variable v2 el resultado debe ser similar a esto
## esperanza mediana varianza coef.asimetría coef.curtosis
## 8.13553061 8.12345506 8.55968058 -0.09074949 0.34968788Variable v3 el resultado debe ser similar a esto
## esperanza mediana varianza coef.asimetría coef.curtosis
## 7.18800000 7.00000000 2.48065600 -0.04139551 -0.238987295.- Considera ahora las variables aleatorias :
v4= 3.v1 - 5
v5= 2.v3-6
Atención : las variables v1 y v3 a las que nos referimos ahora son las obtenidas en el punto 3 ( y analizadas en el 4 ). Son variables aleatorias y no deben confundirse con las que se generaron al principio , en el punto 1 , que eran variables estadísticas
De hecho, si hemos tenido en cuenta la nota técnica del punto 3, v1 y v3 no serán tales , si no las variables aleatorias con el nuevo nombre que les hayamos dado
Teniendo en cuenta las propiedades de los operadores esperanza y varianza, calcular sus medias y varianzas.
Hazlo para tus propios valores ( que serán otros)
ir a punto anterior ir a punto siguiente
E(v4)= 3*E(variable aleatoria 1)-5## [1] 15.832var(v4)= 9*var(variable aleatoria 1)
## [1] 53.46778E(v5)= 2*E(variable aleatoria 3)-5
## [1] 9.376var(v5)= 4*var(variable aleatoria 3)
## [1] 9.9226246.- Construir ahora como variables aleatorias discretas las dos variables anteriores. El proceso será similar al seguido para las variables aleatorias " generadas a partir de v1 v2 y v3 " . en los puntos anteriores .
Primero :Obtendríamos las variables estadísticas como transformaciones de v1 y v3 (consideradas como variables estadísticas) Después: Obtendríamos las distribuciones de frecuencias relativas. Recuperaríamos los recorridos de las dos nuevas variables y construiríamos las distribuciones discretas de probabilidad utilizando la función DiscreteDistribution(). Procederíamos de manera similar al punto 3 Y también representaríamos los gráficos de las dos distribuciones nuevas.
ir a punto anterior ir a punto siguiente
como variables estadísticas
v4<-3*v1-5
v5<-2*v3-6
hist(v4)hist(v5)Tablas de frecuencias absolutas## v4
## 1 4 7 10 13 16 19 22 25 28 31 34 37
## 3 9 25 39 46 39 27 20 18 12 6 5 1## v5
## 0 2 4 6 8 10 12 14 16
## 3 6 27 46 66 46 41 11 4Tablas de frecuencias relativas
## v4
## 1 4 7 10 13 16 19 22 25 28 31 34
## 0.012 0.036 0.100 0.156 0.184 0.156 0.108 0.080 0.072 0.048 0.024 0.020
## 37
## 0.004## v5
## 0 2 4 6 8 10 12 14 16
## 0.012 0.024 0.108 0.184 0.264 0.184 0.164 0.044 0.016Diagramas de barras de las dos nuevas distribuciones de frecuenciasLas convertimos en distribuciones de probabilidad y obtenemos las gráficas de cuantía, distribución y f. cuantiles
Hazlo con tus propios valores.
____________________________________________________
7.- Obtener los principales indicadores de las variables aleatorias v4 y v5 y comprobar que se cumplen las relaciones que obtenidas en el apartado 5.
ir a punto anterior ir a punto siguiente
indicadores y grafiacs de la distribución de v4 ## esperanza mediana varianza coef.asimetría coef.curtosis
## 15.8320000 16.0000000 53.4677760 0.5192085 -0.1921383indicadores y grafiacs de la distribución de v5## esperanza mediana varianza coef.asimetría coef.curtosis
## 8.37600000 8.00000000 9.92262400 -0.04139551 -0.238987298.-Considerar la variable w=v1+v2 obtener su media y su varianza. NO es necesario considerar la nueva variable como variable aleatoria transformación de dos variables aleatorias. Considerémoslas como variables estadísticas. Pero no perdamos de vista que siempre podemos considerarlas como variables aleatorias.
Con toda seguridad la media de W será la suma de las medias de v1 y v2 pero quizá la varianza sea distinta a la suma de las dos varianzas.
Realícese . y contéstese a estas preguntas
¿ a qué se debe? ¿crees que debe pasar lo mismo entre variable aleatorias? ¿cómo lo comprobarías? explícalo.
ir a punto anterior ir a punto siguiente
w<-v1+v2
mean(w)## [1] 15.07953mean(v1); mean(v2)## [1] 6.944## [1] 8.135531var(w)## [1] 16.90366var(v1);var(v2)## [1] 5.964723## [1] 8.594057cov(v1,v2)## [1] 1.172438var(v1)+var(v2)+2*cov(v1,v2)## [1] 16.903669.- Considerar la variable aletoria discreta
definida para los
valores{0,1,2} y cuya función de cuantía obedece
a la
expresión 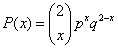
y donde p debe elegirse aleatoriamente como un valor perteciente a [0,1]: p<-runif(1) Obtener su distribucón (generar el objeto) Representar sus gráficos calcular la media , la varianza, la asimetría y la curtosis y la función de cuantía para los tres valores . Hazlo para tus propios valores
ir a punto anterior ir al principio
p<-runif(1)
p## [1] 0.7611418
Indicadores
## esperanza mediana varianza coef.asimetría coef.curtosis
## 1.5222835 2.0000000 0.3636100 -0.8661406 -0.2498004Función de cuantía
Función de cuantía## [1] 0 1 2
## [1] 0.05705326 0.36360997 0.57933677