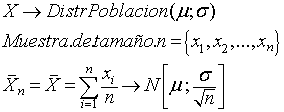La tercera práctica de este curso por razones de
calendario va a ser una amalgama de lo que deberían ser
dos prácticas una primera relacionada con el tema 3
especialmente con el TCL y las distribuciones derivadas de
la distribución normal y una segunda relacionada con el muestreo
y las distribuciones muestrales ( tema 4 )
Primera parte :
Práctica
sobre el TCL ( con ejercicios orientados hacia el muestreo) y
sobre las distribuciones derivadas de la D. normal.
En esta primera parte Trabajaremos con la base de datos coches.sav .Está
constituida por información sobre los supuestos clientes de
una compañia de seguros en el ramo de
automóviles. Consta de 17 variables que informan de
características de clientes y vehículos sobre
un total de 2181 clientes.
La idea de la práctica es la de trabajar sobre el
muestreo de estos datos que , a los efectos (los datos de los 2181 clientes) serán
considerados como poblacionales para comprobar el comportamiento
probabilístico de las muestras.En particular el
comportamiento de la media de una muestra lo suficientemente grande
extraida con reposición (datos independientes).
Puede verse como las variables kilometros, edad del conductor,
edad del vehículo distan mucho de comportarse de forma
parecida a la distribución normal.
Igualmente si
segmentáramos la población en
población de varones y población de mujeres
podríamos ver que esto sigue siendo así en ambos
casos. Sin embargo, la idea es llegar a comprobar la normalidad de las
medias muestrales obtenidas a partir de estos datos poblacionales ( no
normales)
Esta segmentación en dos poblaciones según género puede llevarse
a cabo con la función subset. Y el alumno deberá
hacerlo en algún momento de la práctica
library(foreign, pos=15)
coches <- read.spss("http://www.uv.es/mlejarza/azar/coches.sav", use.value.labels=TRUE,
max.value.labels=Inf, to.data.frame=TRUE)
#nota sobre la carga de datos : se aconseja esta opción de carga para conservar la naturaleza numérica de todos los datos
colnames(coches) <- tolower(colnames(coches))
attach(coches)
names(coches)
## [1] "sexo" "edad" "grupedad" "naños"
## [5] "tipovehiculo" "antigvehiculo" "nsiniest" "costetotal"
## [9] "costemedio" "costemanual" "sinisetropaño" "edadvehiculo"
## [13] "antigcarnet" "kilometros" "nsinultaño" "sinisetro"
## [17] "sin"
summary(kilometros);hist(kilometros)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1380 18593 39137 60237 64376 247320

summary(edad);hist(edad)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 18.0 27.0 32.0 32.9 37.0 60.0

summary(edadvehiculo);hist(edadvehiculo)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.005877 1.000000 2.313298 3.678964 3.853616 16.000000

summary(sexo);plot(sexo)
## varón mujer
## 1072 1109

En Virtud del TCL la media de una muestra aleatoria de
estas variables tenderá
distribuirse con una Normal cuya media será de la
población y cuya desviación típica
será la de la población dividida por la raíz de n (tamaño muestral).
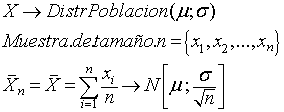
Podemos verlo para una
muestra (con reposición) de tamaño 200 sobre la
variable kilometros (kilómetros recorridos por el
vehículo asegurado)
Para poder trabajar con la distribución de la media
muestral repetiremos un enorme número de veces (200000) la
extracción de la media muestral. De esta forma podemos
obtener una distribución ( de FRECUENCIAS) que se aproxima al
comportamiento aleatorio de la variable “media de una muestra
elegida al azar”
En este caso no hemos fijado ninguna semilla aleatoria. Cada
alumno deberá fijar la suya para realizar sus muestreos
set.seed( 4444)
tamano=200 # tamaño de la muestra
mediamuestral<-as.matrix(NA,ncol=200000,nrow=1)
# definimos la media muestral como #vector de dimensión 200000 ya que vamos a generar ese número de muestras
for(i in 1:200000) {
mediamuestral[i]<-mean(sample(coches$kilometros,tamano))
#así generamos 200000 medias muestrales aleatorias
}
plot(density(mediamuestral))#dibujamos la aproximación continua del histograma de su distribución
# (se parece a la normal como predice el TCL)

media.de.la.media.muestral=mean(mediamuestral);# valor de la media de la distribución
de las medias muestrales
media.de.la.poblacion=mean(coches$kilometros);# media de la población
#según el tcl coinciden los dos valores
desv.tip.de.la.media.muestral=sd(mediamuestral)# desviación típica de la distribución
de las medias muestrales
desv.tipica.de.la.poblacion=sd(coches$kilometros)# desv.tipica de la población
valorteorico.desv.tip.media.muestral=sd(coches$kilometros)/sqrt(tamano);
# valor que según el TCL tiene la desv.tipica de la media muestral
media.de.la.media.muestral
media.de.la.media.muestral## [1] 60230.64
media.de.la.poblacion ## [1] 60237.18
desv.tip.de.la.media.muestral ## [1] 3932.868
desv.tipica.de.la.poblacion ## [1] 58454.87
valorteorico.desv.tip.media.muestral ## [1] 4133.383
Trabajo a realizar:
1.- Contestar a las siguientes preguntas : El objeto mediamuestral ,creado
arriba ¿es un valor escalar? ¿es un vector?
¿es una variable aleatoria? ¿es una variable
estadística? ¿ Son las realizaciones concretas de una
variable aleatoria? ¿es un dataframe?
2.-
Segmentar la población de clientes en clientes hombres y
clientes mujeres. [ ?subset ] (Trabajamos pues con tres bases
de datos)
3.- Primero fijar la semilla aleatoria con el número
correspondiente.Trabajar después con la variable edad del vehiculo; considerar muestras con reposición de tamaño 250 sobre la población total y obtener un número elevado ( 100000)
de muestras y medias muestrales para poder aproximar la
distribución de probabilidad de la media muestral mediante la
distribución de frecuencias de esas medias muestrales.
Comprobar
el cumplimento aproximado del TCL como se ha hecho
más arriba con la variable "kilómetros"
4.- Comentar cómo de buena es la aproximación. ¿mejor que
la del ejemplo "kilómetros"? ¿peor? ¿por qué podría
deberse? ¿hay más error en la media, en la
desviación típica, en el perfil de normalidad?
5.- Manteniendo o fijando de nuevo la semilla aleatoria, si se ha interrumpido la sesión
realizar lo mismo que en 3 y en 4 pero para la variable kilometros en la población de hombres
6.- Considerar las dos poblaciones de hombres y de mujeres y la
variable edad ( Edad de hombres y edad de mujeres, por lo tanto) .
Si
llevamos a cabo dos muestreos independientes uno sobre hombres y otro
sobre mujeres ( consideraremos tamaños distintos 200 y 250
respectivamente)
El TCL garantiza la distribución normal de
las dos medias muestrales por separado.Y la linealiidad de la normal
garantiza que la diferencia de ambas medias también
será normal :
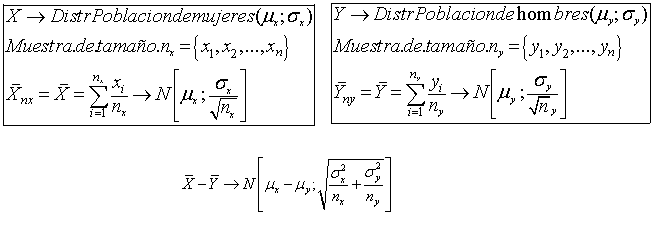
Pues
bien, tras fijar la semilla aleatoria ( o mantenerla fijada) ,
muestrear y obtener suficientes medias muestrales de ambas muestras y
comprobar este resultado de forma similar a los puntos anteriores. MUY IMPORTANTE : LA VARIABLE CON LA QUE SE TRABAJA ES LA "DIFERENCIA DE LAS DOS MEDIAS MUESTRALES", por lo tanto: es necesario que se lleven a cabo un número elevado (100000 por ejemplo , como antes ) de realizaciones muestrales de esa diferencia. Esto hay que tenerlo en cuenta a la hora de diseñar el bucle.
7.-En
una t de Student con 20 g.l. determinar un intervalo que deje una cola
a la izquierda de una probabilidad de 0.15 y una cola a la
derecha de probabilidad 0.25 . Representarlo gráficamente
8.- Hacer lo mismo que en 7 para una Chi-dos con 15 grados de libertad
9- Idem para una F con 10, y 7 grados de libertad
10-
Obtener el p-valor asociado a un valor de 1.75 en un t de Student de 16
grados de libertad, en otra de 20 g.l. y en una normal (tipificada)
.Comentar las diferencias de los resultados
-
Segunda parte : Práctica sobre distribuciones muestrales
Cargaremos los datos de la base de datos
Trabajadores. Se supone que esta formada por la información de
cuatro variables de 250000 trabajadores de cierta provincia. ( Consideramos estos datos poblacionales)
Disponemos información sobre : genero : el genero ( factor) sector : el sector en el que trabaja primario, secundario, terciario ingresos : Los ingresos anuales segurpen: los gastos anuales de cada trabajador en seguros y planes de pensión privados
Consideraremos,
también (aunque no es cierto que la distribución
poblacional de las variables ingresos y segurpen son normales, tanto en la totalidad de
los trabajadores como en cada uno de los grupos ( hombre/mujeres/sector
1/sector2/sector3)
# trabajadores<-read.table("http://www.uv.es/mlejarza/bia/trabajadores.RData") ### La conexión a internet podría ir mal mejor descargar el archivo a equipo local
trabajadores<-read.table("C:/tuubicacion/trabajadores.RData")
summary(trabajadores)
## genero sector ingresos segurpen
## hombre:185500 primario : 13605 Min. : 5084 Min. : 0.0009
## mujer : 64500 secundario: 87169 1st Qu.:19059 1st Qu.: 85.1580
## terciario :149226 Median :22173 Median : 180.5051
## Mean :22096 Mean : 212.7622
## 3rd Qu.:25224 3rd Qu.: 307.7149
## Max. :38265 Max. :1405.9945
Definimos las subpoblaciones de hombres, mujeres, tprimarios, tsecundarios y tterciarios ( Funcion subset)
hombres<-subset(trabajadores, genero== "hombre")
mujeres<-subset(trabajadores,genero=="mujer")
tprimarios<-subset(trabajadores, sector== "primario")
tsecundarios<-subset(trabajadores, sector== "secundario")
tterciarios<-subset(trabajadores, sector== "terciario")
Mediante la función summary(dataframe) obtenderemos las
características de la población total y de las
subpoblaciones
Obtenemos los parámetros
proporcion (poblacional) de distintas cosas (funciones table y
prop.table) la media poblacional de Ingresos y de gastos en seguros (
mean) y la cuasi varianza poblacional de ingresos y de gastos en seguros.
(var) [ mediante el paquete {estadistica} y la instrucción varianza podríamos obtener la varianza]
summary(hombres)
## genero sector ingresos segurpen
## hombre:185500 primario : 9887 Min. : 5084 Min. : 0.0009
## mujer : 0 secundario: 64251 1st Qu.:19050 1st Qu.: 85.1580
## terciario :111362 Median :22285 Median : 180.5469
## Mean :22159 Mean : 212.8358
## 3rd Qu.:25361 3rd Qu.: 307.9565
## Max. :38265 Max. :1405.9945
summary(mujeres)
## genero sector ingresos segurpen
## hombre: 0 primario : 3718 Min. : 5506 Min. : 0.0012
## mujer :64500 secundario:22918 1st Qu.:19078 1st Qu.: 85.1579
## terciario :37864 Median :21882 Median : 180.3710
## Mean :21914 Mean : 212.5506
## 3rd Qu.:24804 3rd Qu.: 307.0508
## Max. :37563 Max. :1141.1006
summary(tprimarios)
## genero sector ingresos segurpen
## hombre:9887 primario :13605 Min. : 7597 Min. : 0.0012
## mujer :3718 secundario: 0 1st Qu.:18136 1st Qu.: 83.4415
## terciario : 0 Median :20770 Median : 176.0954
## Mean :20906 Mean : 209.5560
## 3rd Qu.:23595 3rd Qu.: 305.8292
## Max. :36783 Max. :1022.2109
summary(tsecundarios)
## genero sector ingresos segurpen
## hombre:64251 primario : 0 Min. : 5084 Min. : 0.0009
## mujer :22918 secundario:87169 1st Qu.:18646 1st Qu.: 85.2325
## terciario : 0 Median :21603 Median : 180.0663
## Mean :21637 Mean : 211.9333
## 3rd Qu.:24636 3rd Qu.: 306.7723
## Max. :38265 Max. :1141.1006
summary(tterciarios)
## genero sector ingresos segurpen
## hombre:111362 primario : 0 Min. : 6600 Min. : 0.0057
## mujer : 37864 secundario: 0 1st Qu.:19448 1st Qu.: 85.2686
## terciario :149226 Median :22669 Median : 181.1240
## Mean :22472 Mean : 213.5387
## 3rd Qu.:25638 3rd Qu.: 308.4300
## Max. :37896 Max. :1405.9945
porporciones poblacionales
total
genero.totales<-table (trabajadores$genero)
proporciones.genero.totales<-prop.table(genero.totales)
print("proporciones totales de los dos generos")
proporciones.genero.totales
## [1] "proporciones totales de los dos generos"
##
## hombre mujer
## 0.742 0.258
sector.totales<-table(trabajadores$sector)
proporciones.sector.totales<-prop.table(sector.totales)
print("proporciones totales de los tres sectores")
proporciones.sector.totales
## [1] "proporciones totales de los tres sectores"
##
## primario secundario terciario
## 0.054420 0.348676 0.596904
tabla.cruzada<-table(trabajadores$genero,trabajadores$sector)
tabla.cruzada.por.genero<-prop.table(tabla.cruzada,margin=1)
print("proporciones de cada sector por genero")
tabla.cruzada.por.genero
## [1] "proporciones de cada sector por genero"
##
## primario secundario terciario
## hombre 0.05329919 0.34636658 0.60033423
## mujer 0.05764341 0.35531783 0.58703876
tabla.cruzada.por.sector<-prop.table(tabla.cruzada,margin=2)
print("proporciones de genero en cada sector")
tabla.cruzada.por.sector
## [1] "proporciones de genero en cada sector"
##
## primario secundario terciario
## hombre 0.7267181 0.7370854 0.7462641
## mujer 0.2732819 0.2629146 0.2537359
print("medias y varianzas poblacionales")
print("media y varianza poblacional de Ingresos en el total de trabajadores")
mean(trabajadores$ingresos)
var(trabajadores$ingresos)
## [1] "medias y varianzas poblacionales"
## [1] "media y varianza poblacional de Ingresos en el total de trabajadores"
## [1] 22095.67
## [1] 18110002
print("media y varianza poblacional de gatos.segur. en el total de trabajadores")
mean(trabajadores$segurpen)
var(trabajadores$segurpen)
## [1] "media y varianza poblacional de gatos.segur. en el total de trabajadores"
## [1] 212.7622
## [1] 25552.53
print("media y varianza poblacional de Ingresos en los hombres")
mean(hombres$ingresos)
var(hombres$ingresos)
## [1] "media y varianza poblacional de Ingresos en los hombres"
## [1] 22158.69
## [1] 18610854
print("media y varianza poblacional de gatos.segur. en los hombres")
mean(hombres$segurpen)
var(hombres$segurpen)
## [1] "media y varianza poblacional de gatos.segur. en los hombres"
## [1] 212.8358
## [1] 25609.06
## [1] "de la misma forma se podrían obtener media y varianza poblacionales de las otras subpoblaciones"
Una vez conocidos los valores poblaciones obtenidos arriba nos planteamos ahora el siguiente
Trabajo a realizar:
NOTA PREVIA:SIEMPRE QUE SE LLEVEN A CABO MUESTRAS "EFECTIVAS" CADA ALUMNO DEBE FIJAR SU CORRESPONDIENTE "SEMILLA"
1.- Consideramos muestras aleatorias simples de tamaño 100 sobre el TOTAL DE TRABAJADORES.
a)¿Cuál es la probabilidad de que la proporción de hombres en la muestra esté comprendida entre 0.6 y 0.8 ?
b) Realizar 1000 muestras de ese tamaño y obtener la variable (estadística) proporción muestral de hombres .
Representar el histograma de esta variable ¿se parece a la normal?
c) ¿Cuál es la media de esta variable? ¿y la varianza? ¿ se acercan a los valores teóricos?
d)¿En que proporción de casos está en el rango [0.6,0.8]? Comentar el resultado en relación con los anteriores
2. Suponemos que los ingresos anuales en todos los subgrupos son normales.
Llevamos a cabo una M.A.S. de tamaño 150 sobre los trabajadores del sector terciario y otra (independientemente)
de tamaño 100 sobre los trabajadores del secundario ( se entiende , en ambos casos, que sin distinción de genero).
a) ¿cuál es la probabilidad de que el ingreso medio de los trabajadores secundarios muestreados sea superior a
los de la muestra de trabajadores terciarios?
b) Realizar 1000 veces uno y otro muestreo. Obtener la variable (estadística) diferencia de las dos medias muestrales
Representarla mediante el histograma o su "densidad aproximada" y compararla con la forma que "debería" tener.
c) ¿Cuál es la media de esta variable? ¿Cual es la varianza? ¿ Se aproximan a los valores teóricos?
d) En que proporción de los 1000 casos la diferencia indica que la media de la muestra de trabajadores secundarios
supera a la de trabajadores terciarios. Comentar el resultado en relación con los anteriores
3.- Si muestreamos al azar 100 mujeres y otros tantos hombres .
a) Generemos 1000 veces muestras de 100 de cada género ¿en qué proporción de casos ocurre que la proporción de trabajadores terciarios enrte las mujeres es mayor que entre los hombres ?
Comentar el resultado en relación con los de ejercicios anteriores.
b) Comparar el resultado de a) con la probabilidad de que ocurra según la teoría.
4.- Trabajamos, ahora , con los gastos en seguros y planes de pensiones de hombres y mujeres.( Suponemos normalidad en
ambas poblaciones)
a) Obtener los valores poblacionales de la media y la varianza para ambos conjuntos.
b) Si llevamos a cabo una muestra de tamaño 26 entre los hombres y de tamaño 17 entre las mujeres.
¿Cuál es la probabilidad de que la varianza muestral de las mujeres supere a la de los hombres?
c) Realizar estas dos muestras 1000 veces ¿ en qué proporción ocurre esto?Comentar el resultado en relación con los anteriores
5.- Muestreamos, ahora a 10 trabajadores secundarios ( sin distinción de género)
y consideramos sus gastos en seguros ( que hemos supuesto normales en la población de trabajadores secundarios).
[ Como la muestra es pequeña ( de esto hablaremos en el próximo tema) debemos trabajar con el estadístico t
(apartado 4.3.5. del tema 4 ]
a) ¿Cuál es la probabilidad de que la media de la muestra sea inferior a 210 euros ?
b) Realizadas 1000 muestras , ¿en cuantas ocasiones ocurre esto? Comentar el resultado en relación con los anteriores