1.- El número de personas que entran en una tienda a la hora es una variable aleatoria X con función de cuantía.

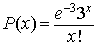
Cuando X  es mayor que cero. Calcular la probabilidad de que en una hora entren en dicha tienda más de dos personas.

Solución sin R

x<-0:50 # en realidad el dominio debería llegar hasta infinito
as.double(x) # la razón de considerarlo double ( o numeric ) 
es que luego no haya problemas con la función exponencial

##  [1]  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22
## [24] 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
## [47] 46 47 48 49 50

personas.en.tienda<-DiscreteDistribution(x ,prob = exp(-3)*3^x/fact(x))
personas.en.tienda

#la función de distribución de 2:  F(2)=P(x=<2) es
p(personas.en.tienda)(2)
## [1] 0.4231901  

# aunque la probabilidad pedida será su complementario P(x>2)=1-F(2)
resultado<-(1-p(personas.en.tienda)(2))
resultado
## [1] 0.5768099

#personas.en.tienda se trata, como veremos en el T3 ,de una distribución de Poisson 
de parámetro(lambda)= 3. Podemos comparar gráficas y probabilidad y ver que coinciden
plot(personas.en.tienda)

plot(Pois(3))

d(personas.en.tienda)(4)
## [1] 0.1680314

dpois(4,lambda = 3)
## [1] 0.1680314

2.- Sea una variable aleatoria comprendida en {0,1,2,3,4,5} con función de cuantía:

P(0)=1/6 

P(x)=1/3- 1/18 x      si x es {1,2,3,4,5}                     determinar la probabilidad: P(2< X =< 4)

Solución sin R

rm(list = ls())#borramos todos los objetos en memoria (ambiente)
X<-DiscreteDistribution(0:5,prob=c(1/6,1/3-1/18,1/3-2/18,1/3-3/18,
                                   1/3-4/18,1/3-5/18))

#La probabilidad P(2< X =< 4)=F(4)-F(2)
p(X)(4)-p(X)(2)
## [1] 0.2777778

3.- Dada una variable aleatoria cuya f. de cuantía viene dada por

x         P(x)

0        0.064

1        0.288 

2        0.432 

3        0.216 

Calcular la media y la varianza

rm(list = ls())#borramos todos los objetos en memoria (ambiente)
X<-DiscreteDistribution(0:3,prob=c(0.064, 0.288, 0.432, 0.216))
E(X) #media o esperanza
## [1] 1.8
var(X)#varianza
## [1] 0.72

4.- El tiempo en segundos que tarda en activarse un dispositivo de alerta cuando se produce cierta anomalía en el sistema sigue una distribución de probabilidad cuya f. de densidad es

f(x)= 2 exp(-2x)        para x >=0

calcular la probabilidad de que tarde entre 3 y 6 décimas 

Solución sin R

rm(list = ls())#borramos todos los objetos en memoria (ambiente)

 
densidad=function(x){
               2*exp(-2*x)}
                   
   #esta es la f.de densidad   cuya gráfica aparece más abajo              

plot(densidad)  

tiempo<-AbscontDistribution(d=densidad,low1=0)
	 #Construimos el objeto tiempo: 
la distribución continua del tiempo que tarde en activarse el dispositivo
 
plot(tiempo) #Dibujamos las funciones de densidad, distribución y f.cantil

sol<-p(tiempo)(.6)-p(tiempo)(.3)#La probabilidad pedida: P(0.3<tiempo<0.6)=F(0.6)-F(0.3)
sol
## [1] 0.2476179

#Otras características de la distribución
E(tiempo) #media
## [1] 0.4999973
var(tiempo) #varianza
## [1] 0.2499884
p(tiempo) (0.6) #f.de distribución de 0.6
## [1] 0.6988037
p(tiempo) (0.3) #f.de distribución de 0.3
## [1] 0.4511857

5.- Dada una v.a. continua definida en [2,3] cuya f.densidad es f(x)=4*x^3/65

determinar la E[3x^2-2x+1]

Solución sin R

rm(list = ls())

dens= function(x) {4*x^3/65}
X<-AbscontDistribution(d=dens,low1=2,up1=3)
plot(X)

E(X)## [1] 2.596194

var(X)## [1] 0.07822221

alfa2<-var(X)+(E(X)^2) # momento ordinario de segundo orden E(X2)

resultado<-3*alfa2-2*E(X)+1;
resultado
## [1] 16.26295