1) Sea una variable aleatoria discreta de recorrido {0,1,2,3,4} y con función de cuantía: 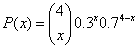cuantía B(4,0.3)

 Representar gráficamente la distribución (Cuantía, distribución y función cuantil) Determinar P(X>1) Determinar (1=< x =< 3) Obtener la esperanza, la varianza, el coef. de asimetría y el de curtosis

x<-0:4
cuantia<-(factorial(4)/(factorial(x)*factorial(4-x)))*0.3^x*0.7^(4-x)

dx0<-DiscreteDistribution(x,cuantia)
plot(dx0)

d(dx0)(2)+d(dx0)(3)+d(dx0)(4) 
## [1] 0.3483
d(dx0)(1)+d(dx0)(2)+d(dx0)(3)
## [1] 0.7518
E(dx0)
## [1] 1.2
var(dx0)
## [1] 0.84
median(dx0)
## [1] 1
## [1] 1
La moda presenta problemas de cálculo pero viendo el gráfico de la f. de cuantía queda claro que la moda es el valor X=1
skewness(dx0)
## [1] 0.4364358
kurtosis(dx0)
## [1] -0.3095238

2  Dada una variable aleatoria continua X pertenecientes a[0,3] con f de densidad 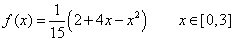             f. de densidad

representar gráficamente la distribución ( densidad, distribución, cuantil) Obtener la media, varianza, asimetría, curtosis, mediana. Determinar P(X<2) Determinar P(X<1) DeterminarP(1<x<2) Determinar un intervalo que cubra el 95% de probabilidad dejando dos colas a ambos lados de 2.5% y 2.5%. 


 
fden<-function (x) {2/15+4/15*x-1/15*x^2}

dx1<-AbscontDistribution(d=fden,low1=0,up1=3)

plot(dx1)

E(dx1)
## [1] 1.649634
var(dx1)
## [1] 0.6376099
skewness(dx1)
## [1] -0.1726425
kurtosis(dx1)
## [1] -1.01897
## [1] -1.01897
median(dx1)
## [1] 1.692834
p(dx1)(2)
## [1] 0.6222222
p(dx1)(1)
## [1] 0.2444445
p(dx1)(2)-p(dx1)(1)
## [1] 0.3777777
q.l(dx1)(0.025)
## [1] 0.1619726
q.l(dx1)(0.975)
## [1] 2.926066
intervalo<-print(paste("[", q.l(dx1)(0.025),",", q.l(dx1)(0.975),"]"))
## [1] "[ 0.161972617506779 , 2.92606639242217 ]"

3) Dada una variable aleatoria continua con X>0 con f de densidad

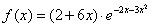
                                                                                                    f. de densidad exponencial-cuadrática

 representar gráficamente la distribución ( densidad, distribución, cuantil) Obtener la media, varianza, asimetría, curtosis, mediana. Determinar P(X<2) Determinar P(X<1) Determinar P(1<2) Determinar un intervalo que cubra el 95% de probabilidad dejando dos colas a ambos lados de 2.5% y 2.5 %. 

fden1<-function(x){(2+6*x)*exp(-2*x-3*x^2)}
dx2<-AbscontDistribution(d=fden1,low1=0)
 plot(dx2) 


E(dx2)
## [1] 0.2957845
var(dx2)
## [1] 0.04865394
skewness(dx2)
## [1] 1.003372
kurtosis(dx2)
## [1] 0.9490969
median(dx2)
## [1] 0.2516114
p(dx2)(2)
## [1] 1
p(dx2)(1)
## [1] 0.9932622
p(dx2)(2)-p(dx2)(1)
## [1] 0.006737835
q.l(dx2)(0.025)
## [1] 0.01242717
q.l(dx2)(0.975)
## [1] 0.824569
intervalo2<-print(paste("[", q.l(dx2)(0.025),",", q.l(dx2)(0.975),"]"))
## [1] "[ 0.0124271699701745 , 0.824568991084167 ]"