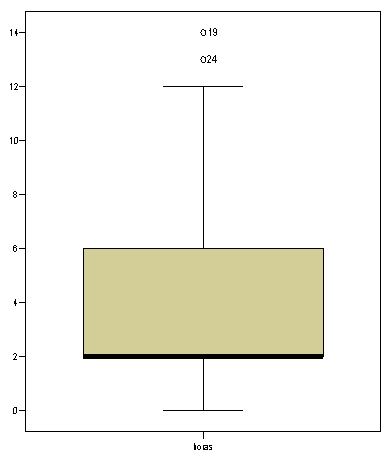1. Tenemos el siguiente juego. Se lanza un dado: si sale un número menor que 3, ganamos 10 EUR; si sale un número mayor que 5, perdemos 5 EUR; en el resto de casos, perdemos 2 EUR. ¿Cuál es la ganancia promedio a la larga?:

A) 1’5 EUR

B) 2 EUR

C) 2’5 EUR

2. Hemos efectuado un experimento en el que se examina el efecto de la dosis de una droga sobre el número de palabras recordadas en un test de memoria. En tal caso, la variable dependiente será:

A) El test de memoria

B) El número de palabras recordadas

C) La dosis de la droga

3. Un psicólogo quiere examinar la duración de las películas del realizador austriaco Michael Haneke. La escala empleada será:

A) De razón

B) De intervalo

C) Ordinal

4. Se analiza la relación entre dos variables medidas en una escala ordinal. Podremos emplear:

A) El coeficiente de Spearman

B) El coeficiente de Kendall

C) Tanto el coeficiente de Spearman como el Kendall

5. La distribución de los datos muestra asimetría negativa. Para lograr una distribución más simétrica efectuaremos una transformación mediante:

A) Cuadrado

B) Logaritmo

C) Puntuaciones típicas

6. Si tenemos 10 datos, la mediana equivaldrá a una media recortada:

A) Al 50%

B) Al 40%

C) Al 60%

7. Lanzamos una moneda 400 veces. Hubo 180 caras y 220 cruces. Siguiendo el criterio del percentil 95 y empleando una prueba de bondad de ajuste con una chi-cuadrado, ¿podemos mantener que hipótesis de que la moneda está equilibrada?:

A) Sí

B) No

C) Las pruebas de bondad de ajuste se efectúan con la prueba t, no con la prueba chi-cuadrado.

8. El coeficiente de correlación de Pearson entre las variables X e Y muestra (virtualmente) una relación positiva perfecta (0’99). ¿Es posible convertir dicho coeficiente en –0’99 mediante una transformación lineal?:

A) Sí, multiplicando cada valor de X por -1

B) No, no es posible

C) Sí, multiplicando cada valor de X y cada valor de Y por -1

9. Sabemos que la recta de regresión de Z a partir de W es Z’=4+0’5W. Sabiendo que las varianzas de Z y de W son 4 y 9, respectivamente, ¿qué proporción de varianza comparten ambas variables?:

A) 0’63

B) 0’75

C) 0’56

10. El gráfico análogo al histograma, pero que conserva los datos brutos, dentro del análisis exploratorio de datos, es:

A) El diagrama de tallo y hojas

B) El diagrama de caja y bigotes

C) El diagrama de sectores

11. Hemos efectuado una prueba que ha proporcionado una t de 3. ¿Cuál sería su valor si hubiésemos hecho una prueba que nos proporcionara una F?:

A) 3

B) 9

C) 6

12. El problema de la colinealidad puede ocurrir:

A) Únicamente en planos/hiperplanos de regresión

B) Únicamente en rectas de regresión

C) Tanto en rectas de regresión como en planos/hiperplanos de regresión

13. Una distribución leptocúrtica tendrá:

A) Un mayor porcentaje de puntuaciones extremas que una distribución normal

B) Un menor porcentaje de puntuaciones extremas que una distribución normal

C) El mismo porcentaje de puntuaciones extremas que una distribución normal

14. En la función de distribución de una variable aleatoria DISCRETA, cada elemento del espacio muestral tiene siempre una probabilidad:

A) igual a 0

B) bien mayor que 0, bien igual a 0

C) mayor que 0

15. Tenemos un test de ansiedad (que sigue la distr.normal) con media 40 y desviación típica 10. ¿Qué proporción de casos tendrán bien una puntuación directa menor de 30, bien una puntuación directa mayor de 60?:

A) 0’1621

B) 0’1815

C) 0’1359

16. Al tratar con variables aleatorias, ¿cuál de los siguientes índices NO refleja propiamente una probabilidad?:

A) Función de densidad de probabilidad

B) Función de probabilidad

C) Función de distribución de probabilidad

17. (TABLA 1) Indica la media recortada al 5%:

A) 4.93

B) 4’64

C) 4’82
18. (TABLA 1) Indica la mediana:

A) Cualquier valor entre 3 y 5

B) Cualquier valor entre 5 y 6

C) 5

19. (TABLA 2) ¿Qué proporción de varianza comparten las variables “nota” y “horas”?

A) 0’93

B) 0’95

C) 0’91

20. (TABLA 2) Por cada hora de estudio, ¿en cuánto se incrementa la nota? (en puntuaciones directas):

A) En 1 punto

B) En 0’953 puntos

C) En 0’976 puntos

21. (TABLA 2) ¿Cuál es la recta de regresión en puntuaciones diferenciales?:

A) nota’=1+0’976horas

B) nota’=0’976horas

C) nota’=0’953horas

22. (TABLA 3) ¿Qué valor de tendencia central ofrecerás, sin efectuar más cálculos, con la información proporcionada?:

A) 3

B) 4

C) 2

23. (TABLA 3) ¿Qué forma tiene la distribución de los datos?:

A) Asimétrica positiva

B) Asimétrica negativa

C) Virtualmente simétrica

24. (TABLA 3) ¿Cuántas “puntuaciones atípicas extremas” hay en los datos?:

A) Ninguna

B) Dos

C) Una

Tabla 1. Datos para la variable “nota”

Frequency Stem & Leaf

5,00 0 . 11223

5,00 0 . 56778

1,00 1 . 0

Stem width: 10

Each leaf: 1 case(s)

Tabla 2. Recta de regression de “nota” a partir de “horas”

Coeficientes(a)

Modelo		Coeficientes no estandarizados		Coeficientes estandarizados	t	Sig.
		B	Error típ.	Beta
1	(Constante)	1,000	,496		2,016	,075
	horas	,976	,104	,953	9,420	,000

a Variable dependiente: nota

Tabla 3. Diagrama de la variable “horas”