Hasta ahora, se ha estudiado la relación existente entre una(s) variable(s) dependiente(s) y n variables independientes x_i (explicativas):
                                                  f: D Í Rⁿ ® R^m

Con el uso de derivadas parciales se estudiaba el comportamiento del fenómeno explicado, y, frente a variaciones infinitesimales de las variables independientes. La variación de y frente a cambios ínfinitesímales de x, viene dado por ¶ y/¶ x_i. Ahora bien, en muchos problemas económicos esta relación no es tan directa. Muchas veces, estas variables explicativas, x_i, dependen a su vez de otras variables independientes:

Supóngase una empresa donde B(y) representa la función de beneficio . Dicha empresa produce un único artículo, x, a partir de un único input, t, con un margen de 10 unidades monetarias por artículo y se sabe que para producir un artículo se requiere 0.5 unidades de input. Así la variación del beneficio, si varían los inputs contratados, será dB/dt = ¶ B/¶ t.

3.- Diferencial de la función compuesta: La regla de la cadena.

Sea f: D_f Í Rⁿ ® R^m / D_f abierto.

Sea g: D_g Í R^m ® R^p / D_g abierto, con f(D_f)Í D_g.

Si f es diferenciable en x₀ Î D_f , y g es diferenciable en y₀ = f(x₀) Î D_g, entonces h =es diferenciable en x₀ cumpliéndose:

Siendo su expresión matricial:

Problemas resueltos

1.- Sean:

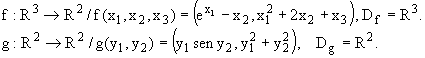
Halle, si existe, la matriz derivada de la función compuesta, es decir, la matriz que represente a la aplicación diferencial de la función compuesta h = en el punto (0,0,0):

Solución:

Comprobación de existencia de la función compuesta y su derivabilidad en el (0,0,0). Es decir, cumplimiento de las hipótesis de la regla de la cadena:

La función f compuesta con g quedaría definida así:

: R^3® R²

¿f es diferenciable en (0,0,0)?

Sí, ya que sus funciones componentes son diferenciables en todos los puntos de R³ por lo que f lo será en todo R³. La primera es suma de una función exponencial con dominio R³ más otra polinómica; y la segunda es polinómica.

0

¿g es diferenciable en f(0,0,0)= (e⁰-0, 0 + 0 + 0) = (1,0)?

Sí, ya que sus funciones componentes son diferenciables en todos los puntos de R² por lo que g lo será en todo R². La primera es el producto de una polinómica por una trigonométrica con dominio R²; y la segunda es polinómica.

Como se cumplen las hipótesis de la regla de la cadena, la función compuesta va a ser diferenciable en el (0,0,0), teniendo como derivada:

y en nuestro caso, al ser funciones vectoriales:

Cálculo de Jf(0,0,0):

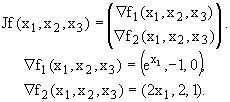
En el (0,0,0) se tiene que

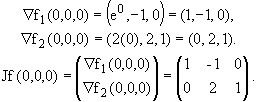
Cálculo de Jg[ f(0,0,0)] =Jg(1,0):

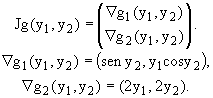
En el (1,0) se tiene que

La matriz jacobiana de la función compuesta resultante es:

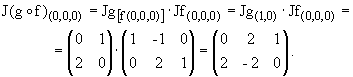
2.- Sea z = sen(xy). Calcule dz/dt, sabiendo que x = e^2t ; y = e^3t .

Solución:

La función compuesta z[(x,y)(t)] = z(t) estaría definida

: R ® R² ® R t ® (x,y) ® z

La función g quedaría así:

Se pide calcular dz/dt. Se cumplen las hipótesis de la regla de la cadena:

• f es diferenciable ya que f₁ y f₂ son diferenciables en R por tratarse de funciones exponenciales definidas en R,
• g es diferenciable en R² por tratarse de una función trigonométrica definida en R².
• Existe función compuesta tal que f(D_f) = f(R)Í D_g = R².

con z'(t) = Ñ g[ f(t)] Jf(t) = Ñ g[ x(t),y(t)] Jf(t) = Ñ g(x,y)_(t) Jf(t) en el punto t.

Cálculo de Jf(t):

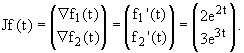
Cálculo de Ñ g(x,y):

En el punto f(t), queda:

Cálculo de Jz(t)

= (e^3t cos(e^5t), e^2t cos(e^5t)) 

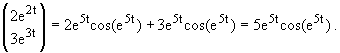
Así pues,

3.- Calcule dz de la siguiente función respecto a x e y:

Calcular dz respecto a x e y equivale a calcular la diferencial de la función compuesta, pues en primera instancia z depende de u y v, pero estas dos variables dependen de x e y. La función compuesta z(x,y) resulta de la composición de las funciones que recoge el enunciado y es una función real de dos variables, (x,y). Llamando f y g a las dos funciones que intervienen, se tiene que:

f es diferenciable en R al serlo las dos funciones componentes, f₁ y f₂, por ser éstas polinómicas,

g: R² ® R

(u,v) ® z(u,v) = (v²+3u)cos(u+3)

g es diferenciable en R² por tratarse del producto de dos funciones diferenciables en R², como lo es (v²+3u), polinómica cuyo dominio es R², y cos(u+3), trigonométrica, cuyo dominio también es R².

La función compuesta resultante es:

: R² ® R² ® R

(x,y) ® (u(x,y),v(x,y)) ® z(u(x,y),v(x,y))

dz(x,y)= d()(x,y)= , por la regla de la cadena se puede calcular la matriz derivada de la diferencial de la función compuestas como el producto de las matrices derivadas que representan a las aplicaciones diferenciales de las dos funciones diferenciables que intervienen en la composición. Así se tiene:

= A_{g[ f(x,y)]} A_f(x,y)

Ñ gf(x,y) = Ñ g[ f(x,y)] Jf(x,y)

Se obtendrá, primero el vector gradiente de g en un punto (u,v) cualquiera. Después se obtendrá el vector de R² que sea imagen de (x,y), es decir, (u(x,y),v(x,y))=f(x,y). Este vector imagen, f(x,y), se sustituye en el vector gradiente de g para obtener la matriz derivada de g en f(x,y), el primer factor del producto de matrices derivadas de arriba. Después se procede a calcular la matriz jacobiana de f en un punto (x,y) sin determinar.

Ñ g[ f(x,y)] = Ñ g[ u(x,y),v(x,y)] = Ñ g[ y²+4, ] =

= (3 cos(y²+7)-(()²+3(y²+4))sen(y²+7), ()cos(y²+7))

Jf(x,y) = 

Ñ (x,y) = Ñ g[ f(x,y)] Jf(x,y) =

= (3 cos(y²+7)-(()²+3(y²+4))sen(y²+7), ()cos(y²+7)) =

=(()cos(y²+7),2y(3cos(y²+7)-(+3(y²+4))sen(y²+7))+()cos(y²+7))

dz(x,y) = ()cos(y²+7)dx +

+(2y(3cos(y²+7)-(+3(y²+4))sen(y²+7))+ ()cos(y²+7))dy

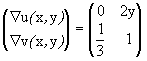
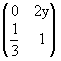4.- Calcule dz de la siguiente función respecto a x e y:

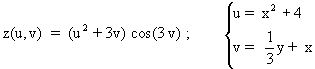
Calcular dz respecto a x e y equivale a calcular la diferencial de la función compuesta, pues en primera instancia z depende de u y v, pero estas dos variables dependen de x e y. La función compuesta z(x,y) resulta de la composición de las funciones que recoge el enunciado y es una función real de dos variables, (x,y). Llamando f y g a las dos funciones que intervienen, se tiene que:

f: R² ® R²

(x,y) ® (u(x,y),v(x,y))=(x²+4, )

f es diferenciable en R al serlo las dos funciones componentes, f₁ y f₂, por ser éstas polinómicas,

g: R² ® R

(u,v) ® z(u,v) = (u²+3v)cos(3v)

g es diferenciable en R² por tratarse del producto de dos funciones diferenciables en R², como lo es (u²+3v), polinómica cuyo dominio es R², y cos(3v), trigonométrica, cuyo dominio también es R².

La función compuesta resultante es:

: R² ® R² ® R

(x,y) ® (u(x,y),v(x,y)) ® z(u(x,y),v(x,y))

dz(x,y)= d()(x,y)= , por la regla de la cadena se puede calcular la matriz derivada de la diferencial de la función compuesta como el producto de las matrices derivadas que representan a las aplicaciones diferenciales de las dos funciones diferenciables que intervienen en la composición. Así se tiene:

= A_{g[ f(x,y)]} A_f(x,y)

Ñ (x,y) = Ñ g[ f(x,y)] Jf(x,y)

Se obtendrá, primero el vector gradiente de g en un punto (u,v) cualquiera. Después se obtendrá el vector de R² que sea imagen de (x,y), es decir, (u(x,y),v(x,y))=f(x,y). Este vector imagen, f(x,y), se sustituye en el vector gradiente de g para obtener la matriz derivada de g en f(x,y), el primer factor del producto de matrices derivadas de arriba. Después se procede a calcular la matriz jacobiana de f en un punto (x,y) sin determinar.

Ñ g[ f(x,y)] = Ñ g[ u(x,y),v(x,y)] = Ñ g[ x²+4,] =

Jf(x,y) = 

Ñ (x,y) = Ñ g[ f(x,y)] Jf(x,y) =

= ((2x²+8)cos(y+3x),3(cos(y+3x)- [ (x²+4)²+(y+3x)] sen(y+3x)) =

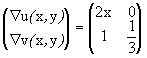
+ (cos(y+3x)-(x²+4)²-(y+3x)sen(y+3x))dy

5.- Calcule dz de la siguiente función respecto a x e y:

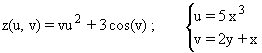
Calcular dz respecto a x e y equivale a calcular la diferencial de la función compuesta, pues en primera instancia z depende de u y v, pero estas dos variables dependen de x e y. La función compuesta z(x,y) resulta de la composición de las funciones que recoge el enunciado y es una función real de dos variables, (x,y). Llamando f y g a las dos funciones que intervienen, se tiene que:

f: R² ® R²

(x,y) ® (u(x,y),v(x,y))=(5x³,2y+x)

f es diferenciable en R² al serlo las dos funciones componentes, f₁ y f₂, por ser éstas polinómicas,

g: R² ® R

(u,v) ® z(u,v) = vu² + 3 cos(v)

g es diferenciable en R² por tratarse de la suma de dos funciones diferenciables en R², como lo es vu², polinómica cuyo dominio es R², y cos(v), trigonométrica, cuyo dominio también es R².

: R² ® R² ® R

(x,y) ® (u(x,y),v(x,y)) ® z(u(x,y),v(x,y))

dz(x,y)= d()(x,y)= , por la regla de la cadena se puede calcular la matriz derivada de la diferencial de la función compuesta como el producto de las matrices derivadas que representan a las aplicaciones diferenciales de las dos funciones diferenciables que intervienen en la composición. Así se tiene:

= A_{g[ f(x,y)]} A_f(x,y)

Ñ (x,y) = Ñ g[ f(x,y)] Jf(x,y)

Se obtendrá, primero el vector gradiente de g en un punto (u,v) cualquiera. Después se obtendrá el vector de R² que sea imagen de (x,y), es decir, (u(x,y),v(x,y))=f(x,y). Este vector imagen, f(x,y), se sustituye en el vector gradiente de g para obtener la matriz derivada de g en f(x,y), el primer factor del producto de matrices derivadas de arriba. Después se procede a calcular la matriz jacobiana de f en un punto (x,y) sin determinar.

Jf(x,y) = 

Ñ (x,y) = Ñ g[ f(x,y)] Jf(x,y) = (20x³y+10x⁴, 25x⁶-3sen(2y+x))=

=(300x⁵y+150x⁶+ 25x⁶-3sen(2y+x), 50x⁶-6sen(2y+x))=

= (300x⁵y+175x⁶-3sen(2y+x), 50x⁶-6sen(2y+x))

6.- Calcule dz de la siguiente función respecto a u y v:

Calcular dz respecto a u y v equivale a calcular la diferencial de la función compuesta, pues en primera instancia z depende de x e y, pero estas dos variables dependen de u y v. La función compuesta z(u,v) resulta de la composición de las funciones que recoge el enunciado y es una función real de dos variables, (u,v). Llamando f y g a las dos funciones que intervienen, se tiene que:

f: R² ® R²

(u,v) ® (x(u,v),y(u,v))=(5u³,2v²+u)

f es diferenciable en R al serlo las dos funciones componentes, f₁ y f₂, por ser éstas polinómicas,

g: R² ® R

(x,y) ® z(x,y) = xy² + 3 cos(y)

g es diferenciable en R² por tratarse de la suma de dos funciones diferenciables en R², como lo es xy², polinómica cuyo dominio es R², y cos(y), trigonométrica, cuyo dominio también es R².

: R² ® R² ® R

(u,v) ® (x(u,v),y(u,v)) ® z(x(u,v),y(u,v))

dz(u,v)= d()(u,v)= , por la regla de la cadena se puede calcular la matriz derivada de la diferencial de la función compuesta como el producto de las matrices derivadas que representan a las aplicaciones diferenciales de las dos funciones diferenciables que intervienen en la composición. Así se tiene:

= A_{g[ f(u,v)]} A_f(u,v)

Ñ (u,v) = Ñ g[ f(u,v)] Jf(u,v)

Se obtendrá, primero el vector gradiente de g en un punto (x,y) cualquiera. Después se obtendrá el vector de R² que sea imagen de (u,v), es decir, (x(u,v),y(u,v))=f(u,v). Este vector imagen, f(u,v), se sustituye en el vector gradiente de g para obtener la matriz derivada de g en f(u,v), el primer factor del producto de matrices derivadas de arriba. Después se procede a calcular la matriz jacobiana de f en un punto (u,v) sin determinar.

Jf(u,v) = 

Ñ (u,v) = Ñ g[ f(u,v)] Jf(u,v) =

= ((2v²+u)²,2(5u³)(2v²+u)-3sen(2v²+u))=

=(15 u² (2v²+u)² +10u³(2v²+u)-3sen(2v²+u), -12v sen(2v²+u))

7.- Calcule de la siguiente función:

Calcular equivale a calcular z’(t), pues la función compuesta que resulta de la composición de las funciones que recoge el enunciado es una función real de variable real. Llamando f y g a las dos funciones que intervienen, se tiene que:

f: R ® R²

t ® (x(t),y(t))=(t², 3t)

f es diferenciable en R al serlo las dos funciones componentes, f₁ y f₂, por ser éstas polinómicas,

g: R² ® R

(x,y) ® z(x,y) = e^x seny

g es diferenciable en R² por tratarse del producto de dos funciones diferenciables en R², como lo es e^x, exponencial cuyo dominio es R², y sen(y), cuyo dominio también es R².

: R ® R² ® R

t ® (x(t),y(t)) ® z(t)

Por todo lo anterior, esta función compuesta es diferenciable en t, y z’(t)=’(t), por la regla de la cadena se puede calcular como el producto de las matrices derivadas que representan a las aplicaciones diferenciales de las dos funciones diferenciables que intervienen en la composición. Así se tiene:

z’(t)= ’(t) = A_{g[ f(t)]} A_f(t) = Ñ g[ f(t)] Jf(t)

Se obtendrá, primero el vector gradiente de g en un punto (x,y) cualquiera, después se obtendrá el vector de R² que sea imagen de t, es decir, (x(t), y(t))=f(t). Este vector imagen, f(t), se sustituye en el vector gradiente de g para obtener la matriz derivada de g en f(t), el primer factor de ese producto. Después se procede a calcular la matriz jacobiana de f en un punto t sin determinar.

Ñ g[ f(t)] = Ñ g[ x(t), y(t)] = Ñ g[ t², 3t] = ()

Jf(t) = 

z’(t) = Ñ g[ f(t)] Jf(t) = ()= 2t + 3 

8.- Calcule de la siguiente función:

Calcular equivale a calcular z’(t), pues la función compuesta que resulta de la composición de las funciones que recoge el enunciado es una función real de variable real. Llamando f y g a las dos funciones que intervienen, se tiene que:

f: R ® R²

t ® (x(t),y(t))=(3t², t+2)

f es diferenciable en R al serlo las dos funciones componentes, f₁ y f₂, por ser éstas polinómicas,

g: R² ® R

(x,y) ® z(x,y) = e^y senx

g es diferenciable en R² por tratarse del producto de dos funciones diferenciables en R², como lo es e^y, exponencial cuyo dominio es R², y sen(x), cuyo dominio también es R².

: R ® R² ® R

t ® (x(t),y(t)) ® z(t)

Por todo lo anterior, esta función compuesta es diferenciable en t, y z’(t)=’(t), por la regla de la cadena se puede calcular como el producto de las matrices derivadas que representan a las aplicaciones diferenciales de las dos funciones diferenciables que intervienen en la composición. Así se tiene:

z’(t)= ’(t) = A_{g[ f(t)]} A_f(t) = Ñ g[ f(t)] Jf(t)

Se obtendrá, primero el vector gradiente de g en un punto (x,y) cualquiera, después se obtendrá el vector de R² que sea imagen de t, es decir, (x(t), y(t))=f(t). Este vector imagen, f(t), se sustituye en el vector gradiente de g para obtener la matriz derivada de g en f(t), el primer factor de ese producto. Después se procede a calcular la matriz jacobiana de f en un punto t sin determinar.

Ñ g[ f(t)] = Ñ g[ x(t), y(t)] = Ñ g[ 3t², t+2] = ()

Jf(t) = 

z’(t) = Ñ g[ f(t)] Jf(t) = ()= 6t + 

Problemas propuestos

1.- Calcule (dz / dt) de la siguiente función:

2.- Calcule (dz / dt) de la siguiente función:

3.- Un individuo tiene una función de utilidad que depende de dos variables : el tiempo que dedica al ocio (x), y el tiempo que dedica al trabajo (y). A su vez estas variables (x,y), dependen de otras dos : el dinero que posee (t₁) y el superávit alimentario que sufre (t₂). Se encuentra en un punto tal que debe dinero a terceros, t₁ = -10, y tiene un superávit alimentarío (calórico) de t₂ = 200. Además, en esta situación se dan las siguientes relaciones marginales:

• Si aumenta una unidad marginal su tiempo de ocio, su nivel de utilidad no se va a alterar.
• Si aumenta una unidad marginal su tiempo de trabajo, su nivel de utilidad va a disminuir en 5 unidades marginales.
• Si aumenta una unidad marginal su dinero, aumentará en una unidad marginal el tiempo que vaya a dedicar al ocio, y disminuirá en 3 unidades marginales el tiempo que vaya a dedicar al trabajo.
• Si aumenta una unidad marginal el superávit alimentario (calórico), aumentará en 2 unidades marginales el tiempo dedicado al ocio, y disminuirá en 2 unidades marginales el tiempo dedicado al trabajo.

1. ¿Qué va a suceder con su nivel de utilidad si varía en una unidad marginal el dinero que posee? ¿Y si varía en una unidad marginal el superávit alimentario?
2. ¿Cuál será, aproximadamente, la variación total (derivada total o diferencial) de la utilidad del individuo si pasa del punto (t₁, t₂)=(-10, 200) al punto (t₁, t₂) =(-10'l, 200'1)?