Los elementos de dicho espacio son vectores columna
 

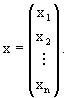
NOTA: Las nociones topológicas siguientes se van a definir en Rⁿ, aunque muchas de ellas no requieren que el conjunto que interviene en las definiciones sea un espacio vectorial.

Producto escalar

En un espacio vectorial real, Rⁿ, se llama producto escalar a una aplicación de Rⁿ´Rⁿ sobre R, que a cada par de vectores x, y de Rⁿ le hace corresponder un número real que se representa por x×y.

Las propiedades que tiene un producto escalar son las siguientes:

- Es definido positivo: x× x > 0, " xÎ Rⁿ.
- Bilineal:     (a x+b y)× z = a (x× z) +b (y× z),
x× (a y+b z) = a (x× y)+b (x× z),
" x,y,zÎ Rⁿ, " a ,b Î R.
- Conmutativo: x× y = y × x " x,yÎ Rⁿ.

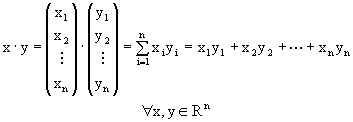
Norma euclídea

Se llama norma de un vector xÎ Rⁿ a una aplicación de Rⁿ sobre R, de forma que a x se le hace corresponder un escalar que se representa por , norma de x, debiendo cumplir dicha aplicación las siguientes propiedades:

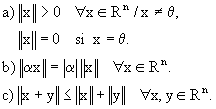
La norma euclídea es una aplicación definida de un espacio euclídeo sobre R, de tal forma que a un vector cualquiera de dicho espacio, xÎ Rⁿ, se le hace corresponder un escalar igual a la raíz cuadrada con signo positivo del producto escalar del vector x por sí mismo, es decir
 

Además de cumplir las tres propiedades anteriores, la norma euclídea cumple una cuarta propiedad:

Distancia (o métrica) euclídea

Se llama métrica o distancia a una aplicación de Rⁿ´Rⁿ sobre R, de forma que al par (x,y)Î Rⁿ´Rⁿ se le asigna un escalar representado por d(x,y), debiendo cumplir dicha aplicación las siguientes propiedades " x,yÎ Rⁿ:

a) d(x,y) > 0 si x¹ y, d(x,y)=0 si x = y;
b) d(x,y) = d(y,x);
c) d(x,z) £ d(x,y) + d(y,z).

Ejemplo:

La distancia del punto (1,2,3) al (0,1,0) es
 

Un espacio métrico es un conjunto en el que se ha definido una métrica o distancia. El que se va a emplear es el formado por Rⁿ y la distancia euclídea, representándolo como (Rⁿ,d), aunque de ahora en adelante cuando se haga referencia a Rⁿ se le estará considerando como un espacio métrico con distancia euclídea.

Bola abierta (entorno abierto)

Se llama bola abierta o entorno abierto de centro aÎ Rⁿ y radio r >0, y se representa por B_r(a) ó B(a,r), al conjunto de vectores de Rⁿ cuya distancia al centro de la bola o del entorno, el punto a, sea menor que el radio r.
 

A través del concepto de bola o entorno se añade el concepto de proximidad y el de límite a la estructura algebraica de un espacio vectorial.

Ejemplos:

En la recta real, en R, una bola abierta es un intervalo abierto:
 

En R² una bola abierta es un círculo sin incluir a la circunferencia que lo limita:
 

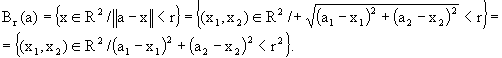
En R³ una bola abierta es una esfera excepto la superficie de la misma.

Bola cerrada (entorno cerrado)

Se llama bola cerrada o entorno cerrado de centro aÎ Rⁿ y radio r >0, y se representa por o por , al conjunto de vectores de Rⁿ cuya distancia al centro de la bola o del entorno, el punto a, sea menor o igual que el radio r.
 

Ejemplos:

En la recta real, en R, una bola cerrada es un intervalo cerrado:
 

En R² una bola cerrada es un círculo completo de centro (a₁, a₂) y radio r.

En R³ una bola cerrada es una esfera completa.

Bola reducida (entorno reducido)

Se llama bola reducida o entorno reducido de centro aÎ Rⁿ y radio r >0, y se representa por B_r*(a) ó B*(a,r), al conjunto de vectores de Rⁿ cuya distancia al centro de la bola o del entorno, el punto a, sea menor que el radio r, excluyendo al centro de la bola, a.
 

Punto interior

Un punto xÎ AÍ Rⁿ se dice que es interior al conjunto A si existe, al menos, una bola abierta centrada en dicho punto que esté totalmente contenida en el conjunto A.
 

Nótese que para que un punto sea interior a un conjunto es condición necesaria que dicho punto pertenezca al conjunto en cuestión.

Así pues, si un punto es interior a un conjunto siempre va a ser posible encontrar un conjunto de puntos suficientemente próximos a él tales que pertenezcan al conjunto A. Cuando se calcule el límite de una función en un punto interior de su dominio, a, se tiene la seguridad de que los puntos x® a van a tener imagen por pertenecer también al dominio.

Interior de un conjunto

Al conjunto de puntos interiores de un conjunto A se le denomina interior de A y se designa por  o por Int(A).

Conjunto abierto

Un conjunto AÍ Rⁿ se dice que es abierto si todos sus puntos son interiores, es decir, si coincide con su interior. También puede decirse que un conjunto A es abierto si no contiene ningún punto que no sea interior a A.

Todas las bolas abiertas son conjuntos abiertos. Rⁿ, incluyendo la recta real R, es un conjunto abierto. El conjunto vacío es también un conjunto abierto porque no existe en el vacío ningún punto que no sea interior.

Ejemplo:

Dado el conjunto A=(1,2] , su interior es Int(A)=(1,2). Sólo pueden ser interiores los puntos pertenecientes al conjunto, por lo que x =1 no es interior a A. El 1’2 sí es interior, ya que para un radio r = 0’1, por ejemplo, se tiene que B_0’1(1’2)Ì A:
 

El punto x =2 no es interior, no existe ningún entorno de puntos próximos a 2 que esté formado exclusivamente por puntos del conjunto A. Esto se justifica porque toda bola abierta centrada en x =2 va a contener puntos mayores que 2 (se encuentran a la derecha del 2), y por tanto no pertenecientes al conjunto A:
 

El conjunto A no es abierto, pues no todos sus puntos son interiores, el punto x=2 no es interior y pertenece al conjunto.

Punto exterior

Un punto xÎ Rⁿ se dice que es exterior al conjunto A si existe una bola abierta (entorno abierto) centrada(o) en dicho punto que no contenga puntos del conjunto A. Es decir, es exterior a A si es interior al complementario de A, A^C={ Rⁿ-A} , téngase en cuenta que AÈ A^C=Rⁿ, AÇ A^C={ Æ } . Suficientemente próximos a un punto exterior de un conjunto sólo se encontrarán puntos no pertenecientes a dicho conjunto.

Exterior de un conjunto

El exterior de un conjunto A es el conjunto de puntos exteriores de A, y se representa con Ext(A).

Ejemplo:

El punto x=0 es exterior al conjunto A=(1,2] , pues para r = 0’5 se tiene que:
 

El punto x =1 no exterior al conjunto A, pues no es interior al complementario de A, es decir, no existe ninguna bola abierta centrada en el punto x =1 que no contenga puntos del conjunto A. En todo entorno centrado en x =1 se encuentra números x >1 (a la derecha de 1) que pertenecen a A.
 

Por tanto el punto x =1 no es exterior al conjunto A, ni tampoco interior como se ha visto antes. Tampoco lo es el punto x =2. Estos puntos que no son ni interiores ni exteriores a un conjunto son los puntos frontera del conjunto.

El exterior de A es
 

Punto frontera

Un punto xÎ Rⁿ se dice que es frontera del conjunto A si toda bola (entorno) centrada(o) en dicho punto contiene puntos del conjunto A y puntos que no pertenecen al conjunto A, es decir, que pertenecen a su complementario. Otra manera de definir un punto frontera de un conjunto A es aquél punto que no es ni exterior ni interior al conjunto A.

xÎ Rⁿ es punto frontera de A si y sólo si
 

Así pues, siempre próximos a un punto frontera de un conjunto donde esté definida una función se encuentran puntos de ese mismo conjunto y puntos que no pertenecen a dicho conjunto. Esto hace que el estudio de las propiedades de continuidad, derivabilidad y diferenciabilidad de funciones en un punto sea diferente en un punto interior que en un punto frontera de uno de los conjuntos cuya unión resulte en el dominio de la función.

Frontera de un conjunto

Al conjunto de los puntos frontera de A se le llama frontera de A y se designa por Fr(A).

Nótese que con relación a un conjunto A todos los puntos de Rⁿ entran en alguna de las tres categorías de puntos: interiores, frontera o exteriores de A. Así, se puede expresar
 

Ejemplo:

Los puntos frontera de A=(1,2] son sólo dos:
 

Como puede verse los puntos frontera se caracterizan por cumplir, al menos, una restricción en términos de igualdad, es decir, el conjunto frontera, o cada uno de los subconjuntos cuya unión constituye la frontera, debe poder caracterizarse con una ecuación, al menos.

Punto adherente

Un punto xÎ Rⁿ se dice que es adherente del conjunto A si toda bola (entorno) centrada(o) en dicho punto contiene puntos del conjunto A.
 

Así pues, siempre próximos a un punto adherente de un conjunto donde esté definida una función se encuentran puntos de ese mismo conjunto.

Todo punto del conjunto A será adherente porque toda bola centrada en dicho punto contiene, al menos, un punto perteneciente a A, el centro de la bola. También se concluye que todo punto frontera de A es adherente, pues la definición de punto frontera garantiza el cumplimiento de la de adherente. Los puntos exteriores no son adherentes.

Adherencia o clausura de un conjunto

Al conjunto de todos los puntos adherentes de un conjunto AÍ Rⁿ se le denomina adherencia o clausura del conjunto A, y se designa por  o por Cl(A). También puede definirse la clausura o adherencia de A como la intersección de todos los conjuntos cerrados que contengan a A. Como la intersección de un número cualquiera de conjuntos cerrados es cerrada, se dice que la adherencia de A es el "menor" conjunto cerrado que contiene a A.

Sabiendo qué puntos son adherentes, la clausura o adherencia de un conjunto A se puede obtener así
 

Ejemplo:

La adherencia de A=(1,2] es
 

Conjunto cerrado

Un conjunto AÍ Rⁿ es cerrado si y sólo si:

- Su complementario es un conjunto abierto.
- Coincide con su adherencia, A = Cl(A), lo que se reduce en la práctica a que
- Todos sus puntos frontera pertenecen al conjunto, Fr(A) Í A.

Toda bola cerrada es un conjunto cerrado. Rⁿ y el vacío, { Æ } , son conjuntos cerrados y abiertos al mismo tiempo (sus complementarios son abiertos y cerrados a la vez).

Algunas propiedades de conjuntos cerrados y abiertos

1.- La unión de cualquier número de conjuntos abiertos es abierta, incluso la unión infinita de conjuntos abiertos.

2.- La intersección de un número finito de conjuntos abiertos es abierta.

3.- La unión de un número finito de conjuntos cerrados es cerrada.

4.- La intersección de un número cualquiera de conjuntos cerrados es cerrada.

5.- Si el conjunto A es abierto y B es cerrado, entonces A-B es un conjunto abierto y B-A es un conjunto cerrado.

Punto de acumulación

Un punto xÎ Rⁿ se dice que es de acumulación del conjunto A si toda bola (entorno) reducida(o) centrada(o) en dicho punto contiene puntos del conjunto A.
 

Así pues, siempre próximos a un punto de acumulación de un conjunto donde esté definida una función se encuentran puntos de ese mismo conjunto distintos al centro de la bola.

Todo punto interior del conjunto A es de acumulación porque toda bola (entorno) reducida(o) centrada(o) en dicho punto contiene infinitos puntos pertenecientes a A distintos del centro de la bola. Como para un punto interior es posible encontrar un conjunto de infinitos puntos suficientemente próximos a él pertenecientes al conjunto, toda bola o entorno centrada en ese mismo punto contiene siempre a todos o a parte de esos infinitos puntos, por lo que se verifica la definición de punto de acumulación. Alrededor de ese punto interior se "acumulan" puntos del conjunto. Sin embargo, no está garantizado que todo punto frontera de A sea de acumulación, pues la definición de punto frontera garantiza el cumplimiento de la de adherente, pero un punto adherente no es necesariamente de acumulación. Los puntos exteriores no son de acumulación.

Es interesante resaltar que cuando se plantee el cálculo del límite de una función en un punto x, dicho punto va a ser un punto de acumulación del dominio de la función, para tener garantizada la existencia de imágenes reales para los puntos próximos a x, ya que pertenecerán también al dominio.

Punto aislado

Un punto xÎ AÌ Rⁿ se dice que es o está aislado del conjunto A si existe una bola (entorno) reducida(o) centrada(o) en dicho punto que no contiene puntos del conjunto A.
 

Así pues, para distancias lo suficientemente pequeñas, alrededor de un punto aislado no se va a encontrar ningún otro punto del conjunto. Así pues, para estudiar en la práctica las propiedades de continuidad, derivabilidad y diferenciabilidad de una función en un punto, no sólo hay que conocer si se trata de un punto interior o de un punto frontera, sino que además, en el caso de que sea frontera hay que determinar si es o no un punto aislado del dominio o de alguno de los conjuntos cuya unión forme el dominio.

Está claro por la definición de punto aislado que ningún punto interior lo es, así como que todo punto aislado es un punto frontera.

Conjunto derivado

Al conjunto de todos los puntos de acumulación de un conjunto AÍ Rⁿ se le denomina conjunto derivado del conjunto A, y se designa por A’.

Con la definición de punto de acumulación se tiene una nueva caracterización de conjunto cerrado:
 

Sabiendo qué puntos son y pueden ser de acumulación, el conjunto derivado de un conjunto A se puede obtener así
 

Ejemplos:

El conjunto derivado de A=(1,2] es
 

Como Int(A) =(1, 2), Fr(A)={ 1, 2} , { conjunto de puntos aislados de A} ={ Æ } ,

se tiene que A’=[ 1,2] .

El conjunto derivado de B={ 1,2,3} es el vacío, pues el conjunto B no tiene ningún punto interior, sólo consta de un número finito de puntos, tres puntos aislados, por lo que no puede contener ninguna bola con infinitos puntos.
 

x =1 es un punto aislado de B ya que para r = 0’5 se tiene que B_r*(1)Ç B={ Æ } :
 

De forma análoga se justificaría que x=2, y que x=3 son puntos aislados de B.

1.- Halle el interior y el conjunto frontera de :

a)
b)
c)
d)

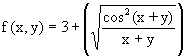
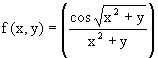
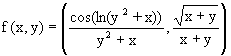
Representación gráfica del conjunto A :
 

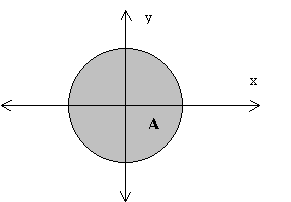
El interior de A es el círculo sin incluir la circunferencia:
 

La frontera es la circunferencia que delimita el círculo:
 

Por tanto, como Fr(A)Ì A el conjunto es cerrado y no es abierto porque no todos sus puntos son interiores (los de la circunferencia).

b) B={ (0,4)} está formado por un único punto que es un punto aislado de B. El interior de B es el vacío y la frontera de B coincide con el conjunto, Fr(B)=B. Se trata de un conjunto cerrado pues Fr(B)Ì B.

c) C es el producto cartesiano de dos intervalos, caracterizado con inecuaciones o desigualdades queda así:
 
 

Representación gráfica del conjunto C:

El interior de C es el cuadrado sin incluir los lados del mismo:
 

La frontera son los cuatro lados del cuadrado:
 

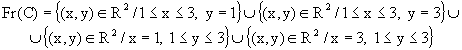
Por tanto, como Fr(A)Ë A el conjunto no es cerrado y no es abierto porque no todos sus puntos son interiores (dos lados del cuadrado).

2.-
a) El dominio de la función es D_f ={ (x,y)Î R²/ f(x,y) Î R} . La expresión de f(x,y) es el logaritmo neperiano de un cociente de dos funciones reales de dos variables. El logaritmo neperiano no está definido para números reales no positivos. Por tanto, los puntos (x,y) Î R² que proporcionen un argumento positivo para la función logaritmo serán los puntos del dominio de esta función. El argumento de ese logaritmo es un cociente, como ya se ha dicho. El numerador,, es un número real no negativo " (x,y) Î R², pues para cada punto se obtiene un radicando no negativo, al ser la suma de dos números reales no negativos por estar elevados al cuadrado, y la raíz cuadrada se está considerando con signo positivo. El numerador sólo se anulará en el (0,0). El denominador es un número real que puede tomar cualquier signo, " (x,y) Î R², 2x + y. El cociente de dos números reales es otro número real si el denominador no es cero, y esto sucede si 2x+y¹ 0, que también descarta al (0,0) que era el único punto que anulaba el numerador. Por tanto, teniendo en cuenta que ese cociente debe ser positivo, ya que es el argumento de una función logaritmo, el dominio de la función es:
 

Un conjunto es cerrado si incluye a sus puntos frontera. La frontera de este conjunto es
 

Estos puntos son frontera del dominio de la función porque toda bola o entorno centrado en ellos contiene puntos del dominio y puntos que no pertenecen al dominio de la función.

Como puede apreciarse Fr(D_f )Ë D_f , por lo que D_f no es cerrado. Sí es un conjunto abierto porque todos sus puntos son interiores (la restricción que lo caracteriza es estricta) o bien porque su complementario es cerrado al incluir a sus puntos frontera:
 
 

b) El dominio de la función es D_f ={ (x,y)Î R²/ f(x,y) Î R} . f(x,y) es la suma de una constante, 3, más la raíz cuadrada de un cociente de dos funciones. El resultado será un número real si la raíz cuadrada lo es. Para ello, el radicando debe ser no negativo. El radicando es el cociente de dos funciones. En el numerador se tiene el cos²(x+y) que es un número real no negativo " (x,y) Î R², en concreto, comprendido entre 0 y 1. El denominador es la suma de dos números reales, x + y. Para que el cociente sea un número real el denominador debe ser distinto de cero, x + y ¹ 0. Para que, además, el cociente sea un número real no negativo, el denominador deberá ser positivo, ya que el numerador es mayor o igual a 0. Por tanto, teniendo en cuenta todo esto, el dominio de la función es:
 

Un conjunto es cerrado si incluye a sus puntos frontera. La frontera de este conjunto es
 

Estos puntos son frontera del dominio de la función porque toda bola o entorno centrado en ellos contiene puntos del dominio y puntos que no pertenecen al dominio de función.

Como puede apreciarse Fr(D_f )Ë D_f , por lo que D_f no es cerrado. Sí es un conjunto abierto porque todos sus puntos son interiores (la restricción que lo caracteriza es estricta) o bien porque su complementario es cerrado al incluir a sus puntos frontera:
 
 

c) El dominio de la función es D_f ={ (x,y)Î R²/ f(x,y) Î R} . f(x,y) es el cociente de una función trigonométrica dividido por una función polinómica. El argumento de la función trigonométrica es la raíz cuadrada del mismo polinomio que actúa como denominador. El radicando, x²+y, de la raíz que actúa como ángulo de la función coseno devuelve un número real siempre. Para que el ángulo sea un número real, y por tanto, tenga imagen real en la función coseno, se requiere que el radicando sea no negativo, x²+y ³ 0. La función coseno devuelve un número real para cualquier ángulo real. El cociente de dos números reales es otro número real siempre que el denominador no sea cero, por tanto, hay que exigir que , x²+y ¹ 0. Por tanto, teniendo en cuenta todo esto, el dominio de la función es:
 

Un conjunto es cerrado si incluye a sus puntos frontera. La frontera de este conjunto es
 

Como puede apreciarse Fr(D_f )Ë D_f , por lo que D_f no es cerrado. Sí es un conjunto abierto porque todos sus puntos son interiores (la restricción que lo caracteriza es estricta) o bien porque su complementario es cerrado al incluir a sus puntos frontera:
 

d) Se trata de una función vectorial, por lo que su dominio es la intersección de los dominios de las dos funciones componentes D_f = D_1Ç D₂. La primera función componente f₁(x,y) es el cociente de una función trigonométrica dividido por una función polinómica. El argumento (o ángulo) de la función trigonométrica es el logaritmo neperiano del mismo polinomio que actúa como denominador en ese cociente. La función logaritmo siempre devuelve un número real para los puntos donde esté definida. Para que el logaritmo neperiano esté definido, se requiere que su argumento sea un número real positivo, y²+x > 0. La función coseno devuelve un número real para cualquier ángulo real. El cociente de dos números reales es otro número real siempre que el denominador no sea cero, por tanto, hay que exigir que , y²+x ¹ 0. Teniendo en cuenta todo esto, el dominio de la función es:
 
 

Un conjunto es cerrado si incluye a sus puntos frontera. La frontera de este conjunto es
 

Estos puntos son frontera del dominio de la función porque toda bola o entorno centrado en ellos contiene puntos del dominio y puntos que no pertenecen al dominio de la función f₁.

Como puede apreciarse Fr(D₁ )Ë D₁ , por lo que D₁ no es cerrado. Sí es un conjunto abierto porque todos sus puntos son interiores (la restricción que lo caracteriza es estricta) o bien porque su complementario es cerrado al incluir a sus puntos frontera:
 
 

El dominio de la segunda función componente es D₂ ={ (x,y)Î R²/ f₂(x,y) Î R} . f₂(x,y) es un cociente de dos funciones reales de dos variables. El numerador,, es un número real si x+y ³ 0. El denominador es un número real " (x,y) Î R². El cociente de dos números reales es otro número real si el denominador no es cero, y esto sucede si x+y¹ 0. Por tanto, teniendo en cuenta todo lo dicho, el dominio de la función es:
 
 

La frontera de este conjunto es
 

La función f(x,y) tiene como dominio
 

Al tratarse de la intersección de dos conjuntos abiertos es otro conjunto abierto. En general, la frontera del dominio de una función vectorial no es ni la intersección ni la unión de los conjuntos frontera de los dominios de las funciones componentes, por lo que hay que tener especial cuidado a la hora de calcular la frontera.
 
 

Adicionalmente a las referencias recogidas en el documento de "Esquemas y referencias bibliográficas" se ha utilizado la siguiente bibliografía:

APOSTOL, T.M. (1976).- "Análisis matemático", pp.57-89. Reverté. Barcelona.

BARTLE, R.G. (1980).- "Introducción al análisis matemático", pp. 73-103. Limusa. México.

DE BURGOS, J. (1984).- "Cáculo infinitesimal: teoría y problemas", pp.46-60 y 78-102. Alhambra Universidad, Madrid.