Rafael Pla-Lopez
Department of Applied Mathematic
Universitat de València, Spain
Abstract
A statistical approach to the traveler's dilemma, first searching the better results from a equiprobabilistic distribution of answers, after making an iterative process, by supposing the frequency of a answer is proportional to its result (genetic iteration) and by supposing the people select the prior better answers (rational iteration).
Introduction
In the August 2007 issue of
"Investigación y Ciencia" (the Spanish edition of
"Scientific American") I read an article about the traveler's
dilemma by Kaushik Basu (two travelers who have lost the same
object claim an indemnity; the company ask them separately its price,
warning them that if they say the same quantity, between 2 and 100
€, both will receive this quantity, but if they say different
quantities, the company will accept the lower quantity, but they will
give this quantity plus 2 € as a bonus to the traveler who had
said the lower quantity, and this quantity minus 2 € as a
penalization to the traveler who had said the higher quantity). The
professor Basy explains that the only Nash's equilibrium, corresponding
to the standard Game Theory, so that nobody can improve its results by
an unilateral change, is the situation in which both travelers answer 2
€. Nevertheless, this answer is very inefficient and unusual.
And therefore the Theory would have to change to solve this paradox.
Because I was in my free month, I could devote time to this problem, far of my usual field of research in modelization of social evolution. I began by asking to the members of my family. So, my wife, a teacher, gave me the Nash's standard suspicious answer, 2 €. And my young son gave me the intuitive trusting answer, 100 €. So, I decided to make a statistical modelling approach.
Because I was in my free month, I could devote time to this problem, far of my usual field of research in modelization of social evolution. I began by asking to the members of my family. So, my wife, a teacher, gave me the Nash's standard suspicious answer, 2 €. And my young son gave me the intuitive trusting answer, 100 €. So, I decided to make a statistical modelling approach.
First approach from
equiprobability
I suppose the first traveler, A, faces up with other 99 travelers, and each one of them give a different answer x between 2 and 100. So, we can calculate the average result of the answer y of the traveler A,
I suppose the first traveler, A, faces up with other 99 travelers, and each one of them give a different answer x between 2 and 100. So, we can calculate the average result of the answer y of the traveler A,
A1(y)
= [ SUM x=2:y-1 (x-2) + y + SUM
x=y+1:100 (y+2) ]/99 = [ (y-2)(0+y-3)/2 + y + (100-y)(y+2)
]/99 =
= (-y2 + 193y + 406)/198
= (-y2 + 193y + 406)/198
|
You can see in Figure
1 this average result A1
as a function of the answer y.
We get the maximum result by solving dA1/dy = (-2y+193)/198 = 0 which corresponds to y=193/2=96.5 : the most near integer values y=96 and y=97 have the same average result of 49.080808 |
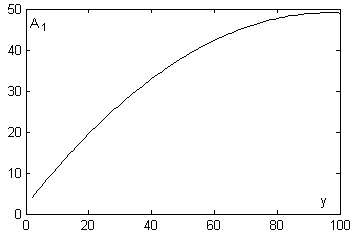 Figure 1
Average results face up equiprobabilistic answers |
Genetic iteration
We can suppose that, in successive occasions, the answers which have got better results will happen which more frequency. In order to model this process, we will suppose that the frequency of a answer is proportional to its previous average result.
So, we have the following iterative relation:
An+1(y) = [SUM x=2:y-1 An(x)(x-2) + An(y)y + SUM x=y+1:100 An(x)(y+2)] / SUM x=2:100 An(x)
You can see in Figure 2 the last average results of A as a function of its answer y through this genetic iteration, compared whith the initial approach: y=96 is consolidated as the better answer, with an average result which arrive about 61 €.
Note that the travelers don't need know the calculation of the better answer through this genetic iteration: the better answers just spread more easily.
We can suppose that, in successive occasions, the answers which have got better results will happen which more frequency. In order to model this process, we will suppose that the frequency of a answer is proportional to its previous average result.
So, we have the following iterative relation:
An+1(y) = [SUM x=2:y-1 An(x)(x-2) + An(y)y + SUM x=y+1:100 An(x)(y+2)] / SUM x=2:100 An(x)
I've implemented this iteration in language C (you can get the source code in http://www.uv.es/pla/models/viajero/viajero.c) and got the successive maximum average results from integer answers, which are: n= 1: A(96)=49.080807 A(97)=49.080807 n= 2: A(96)=59.993732 n= 3: A(96)=60.926846 n= 4: A(96)=61.021133 n= 5: A(96)=61.031261 n= 6: A(96)=61.032364 n= 7: A(96)=61.032497 n= 8: A(96)=61.032520 n= 9: A(96)=61.032509 n=10: A(96)=61.032516 n=11: A(96)=61.032509 n=12: A(96)=61.032513 n=13: A(96)=61.032524 n=14: A(96)=61.032513 n=15: A(96)=61.032524 (from n=13 the results happen again cyclically) |
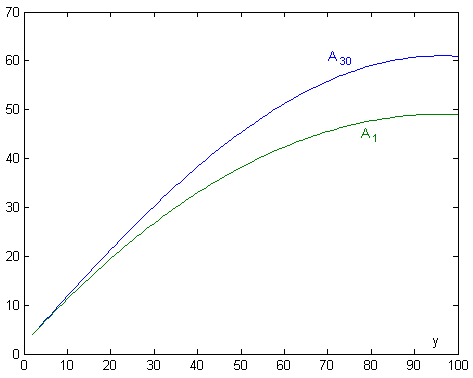 Figure 2
Average results in the first step (green) and in the 30th step (blue) |
You can see in Figure 2 the last average results of A as a function of its answer y through this genetic iteration, compared whith the initial approach: y=96 is consolidated as the better answer, with an average result which arrive about 61 €.
Note that the travelers don't need know the calculation of the better answer through this genetic iteration: the better answers just spread more easily.
Rational iteration
We will suppose now that the travelers know in each step the calculation of the average results, and choose the better answers by rounding to integer numbers both answers and results.
So, in the first step 48.5 ≤ A1(y) < 49.5 if and only if 86≤y≤100, and we can suppose that in the second step the only answers of the other travelers are x=86:100, and therefore the average results will be
A*2(y) = [ SUM x=86:y-1 (x-2) + y + SUM x=y+1:100 (y+2) ]/15 = [(y-86)(84+y-3)/2 + y + (100-y)(y+2)]/15 =
= (-y2 + 193y - 6566)/30
By solving
dA*2/dy = (-2y+193)/30 = 0
we get the same value y=193/2=96.5 for the maximum result (in fact, we would get the same value provided that the answers x vary from any number to 100), but now the average result for y=96 and y=97 is 91.53333, which approach to 92, and every other answer get an average result lesser than 91.5.
So, in the third step we can suppose that the answers of the other travelers are x=96 or x=97. We can repeat the calculation, but with only two answers we can calculate directly their average results:
A*3(96) = (96+98)/2 = 97
A*3(97) = (94+97)/2 = 95.5
Therefore, the better answer is unequivocally y=96. In fact, with only two answers y=96 is a dominant option (it get the better result independently of the answer of the another traveler), and the statistical forecast agrees with the Nash's equilibrium.
So, both the genetic iteration and the rational iteration arrive to the same conclusion: the better answer is 96 €. Nevertheless, the rational iteration obtains a greater result, 97 in front of 61.
We will suppose now that the travelers know in each step the calculation of the average results, and choose the better answers by rounding to integer numbers both answers and results.
So, in the first step 48.5 ≤ A1(y) < 49.5 if and only if 86≤y≤100, and we can suppose that in the second step the only answers of the other travelers are x=86:100, and therefore the average results will be
A*2(y) = [ SUM x=86:y-1 (x-2) + y + SUM x=y+1:100 (y+2) ]/15 = [(y-86)(84+y-3)/2 + y + (100-y)(y+2)]/15 =
= (-y2 + 193y - 6566)/30
By solving
dA*2/dy = (-2y+193)/30 = 0
we get the same value y=193/2=96.5 for the maximum result (in fact, we would get the same value provided that the answers x vary from any number to 100), but now the average result for y=96 and y=97 is 91.53333, which approach to 92, and every other answer get an average result lesser than 91.5.
So, in the third step we can suppose that the answers of the other travelers are x=96 or x=97. We can repeat the calculation, but with only two answers we can calculate directly their average results:
A*3(96) = (96+98)/2 = 97
A*3(97) = (94+97)/2 = 95.5
Therefore, the better answer is unequivocally y=96. In fact, with only two answers y=96 is a dominant option (it get the better result independently of the answer of the another traveler), and the statistical forecast agrees with the Nash's equilibrium.
So, both the genetic iteration and the rational iteration arrive to the same conclusion: the better answer is 96 €. Nevertheless, the rational iteration obtains a greater result, 97 in front of 61.
Bibliography
Kaushik Basu, "El dilema del viajero", Investigación y Ciencia, August 2007, pages 48-54
 This article can be reproduced and republished freely, in whole or in part, by giving the reference http://www.uv.es/pla/models/viajero
This article can be reproduced and republished freely, in whole or in part, by giving the reference http://www.uv.es/pla/models/viajero
Kaushik Basu, "El dilema del viajero", Investigación y Ciencia, August 2007, pages 48-54
 This article can be reproduced and republished freely, in whole or in part, by giving the reference http://www.uv.es/pla/models/viajero
This article can be reproduced and republished freely, in whole or in part, by giving the reference http://www.uv.es/pla/models/viajero