| posició | cand.A | cand.B |
| 1 | 33/1=33 | 67/1=67 |
| 2 | 33/3=11 | 67/3=22'33 |
| posició | cand.A | cand.B |
| 1 | 33/1=33 | 67/1=67 |
| 2 | 33/2=16'5 | 67/2=33'5 |
Per a comparar el grau de proporcionalitat de diferents sistemes electorals haurem de comparar les respectives distàncies entre las corresponents distribucions de llocs i la distribució de les proporcions exactes.
Suposem que hi ha r candidatures per a n llocs amb unes proporcions de vots P=(p1, p2,..., pr ), que amb un determinat sistema electoral obtenen respectivament M=(m1, m2,..., mr) llocs, y que amb altre sistema electoral obtenen M'=(m'1, m'2,..., m'r) llocs. Essent la proporció exacta de llocs a les diferents candidatures n·P=(n·p1, n·p2,..., n·pr ), direm que el primer sistema té un grau de proporcionalitat major que el segon si per a qualsevol proporcions P de vots la distància entre M i n·P és menor o igual a la distància entre M' i n·P, d(M,n·P)£d(M',n·P) , i per alguna proporció P de vots d(M,n·P)<d(M',n·P) . La distància entre dos vectors ve donada per la norma de la seua diferència, és a dir d(M,n·P)=|M-n·P)| i d(M',n·P)=|M'-n·P|.
Demostrarem
que el sistema de Resta Major és el sistema amb major grau de proporcionalitat
amb qualsevol número de candidatures per a les normes usuals.
2 candidatures:
Observem
que en el cas de 2 candidatures la demostració és trivial:
si una candidatura té n·p1=s1+e1,
amb s1 enter i 0£e1<1,
i altra té n·p2=s2+e2,
amb s2 enter i 0£e2<1,
essent e1<e2
. A no ser que les proporcions exactes n·p1
i n·p2 siguen
números enters, cas en el qual e1=e2=0,
s'acomplirà e1+e2=1
i el sistema de Resta Major assignarà s1
llocs a la primera candidatura i s2+1
llocs a la segona candidatura. Aleshores la diferència entre llocs
obtinguts i la seua proporció exacta serà M-n·P=(e1,1-e2)=(e1,e1).
Si pel contrari s'assignara s1+1
llocs a la primera candidatura i s2
llocs a la segona, la diferència seria M'-n·P=(1-e1,e2)=(e2,e2).
Com e1<e2,
la norma del primer vector és menor que la del segon amb qualsevol
definició de la mateixa. Qualsevol altra distribució de llocs
ni tan sols seria estrictament proporcional, i la seua distància
a les proporcions exactes seria encara major (de fet, seria major que (1,1)).
Norma-1:
Suposem ara el cas general de r candidatures. Començarem aplicant una de les normes més senzilles, la norma-1, definida per |(x1,x2,...,xr)|1=Si=1:r |xi| . Suposem que M=(m1, m2,..., mr) és una distribució de llocs pel sistema de Resta Major. Suposem que les seues restes són e1³e2³...³er i que després d'haver assignat a cada candidatura la seua part entera queden k llocs per distribuir. Aleshores la distància entre les proporcions exactes i la distribució de llocs serà
Qualsevol canvi en la distribució dels k llocs pendents que no corresponga a una distribució pel sistema de Resta Major i que respecte la proporcionalitat estricta suposarà que algunes candidatures j£k perden un lloc i algunes candidatures t>k guanyen un lloc, essent ej>et , de manera que a la distància entre les proporcions exactes i la distribució de llocs caldrà restar-li (1-ej)+et i sumar-li ej+(1-et) . Per tant, per cada canvi aquesta distància tindrà un increment de
Naturalment,
una distribució que no respecte la proporcionalitat estricta tindria
un increment encara major. Per tant, qualsevol distribució que altere
la proporcionada pel sistema de Resta Major augmenta la distància
entre la distribució de llocs i les proporcions exactes. Per tant,
utilitzant la norma-1 el sistema de Resta Major és el que té
un major grau de proporcionalitat.
Norma-2:
Si apliquem la norma-2 o norma euclídea, definida per |(x1,x2,...,xr)|2=ÖSi=1:r |xi|2 , la distància entre les proporcions exactes i la distribució indicada per Resta Major serà
Qualsevol canvi de llocs que vulnere la distribució per Resta Major, entre candidatures j£k i t>k tals que ej>et , suposarà un increment del quadrat de la distància igual a
Norma-a:
Podem ara generalitzar els resultats per a qualsevol norma-a, definida per |(x1,x2,...,xr)|a=(Si=1:r |xi|a)1/a per a qualsevol número real positiu a, de la qual són casos particulars la norma-1 i la norma-2. En aquest cas l'increment de la potència a de la distància per qualsevol canvi de llocs que vulnere la distribució per Resta Major, amb ej>et , serà
Ara bé, és fàcil comprovar que ea-(1-e)a augmenta quan augmenta e. En efecte, la seua derivada respecte a e és
Per
tant, el referit increment de la potència a
de la distància serà positiu, la distància augmentarà
al vulnerar-se la distribució per Resta Major, i el sistema de Resta
Major és el que té un major grau de proporcionalitat amb
la norma-a
per a qualsevol a>0
.
Norma-¥:
Per tal com la norma-¥ , definida per |(x1,x2,...,xr)|a=màxim(|xi|)i=1:r , és el límit de la norma-a quan a tendeix a infinit, podriem extrapolar per a la mateixa el resultat anterior. Podem, en qualsevol cas, demostrar-ho també directament.
El vector de les diferències entre les proporcions exactes i la distribució indicada per Resta Major serà
Per tal com 1-e1£1-e2£...£1-ek i ek+1³...³er, la seua norma infinit serà
ESTUDI DE CASOS PARTICULARS AMB 2 CANDIDATURES:
Estudiarem ara alguns casos d'aplicació del sistema de Resta Major, Saint Lagué i Regla d'Hondt amb 2 candidatures, representant per punts en el plà tant les proporcions exactes com les distribucions de llocs pels diferents sistemes. En particular, assenyalarem per un asterisc el punt que represente les proporcions exactes, per una creu el punt que represente la distribució per Resta Major i Saint Lagué (que, com podrem comprovar, amb 2 candidatures donen sempre el mateix resultat), i per una aspa el punt que represente la distribució per Regla d'Hondt. Per a major claredat estudiarem casos "fronterers", és a dir, aquells que amb el canvi d'1 vot es produiria un empat i amb el canvi de 2 vots variaria la distribució en 1 lloc.
1. Casos en que amb 2 vots més la candidatura minoritària obtendria 1 lloc també amb Regla d'Hondt:
1.1.
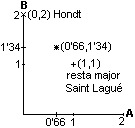
Per a distribuir 2 llocs entre 2 candidatures amb 33 i 67 vots respectivament:
Total de vots a candidatures:
33+67=100
Candidatura A: 33 vots;
proporció exacta: 2x33/100=0'66
Candidatura B: 67 vots;
proporció exacta: 2x67/100=1'34: punt (0'66,1'34)
Distribució per Resta
Major o Saint Lagué: 1 per a A i 1 per a B: punt (1,1). Veure Tabla
1.1.a
Distribució per Regla
d'Hondt: 0 per a A i 2 per a B: punt (0,2). Veure Tabla 1.1.b
|
|

|
1.2.
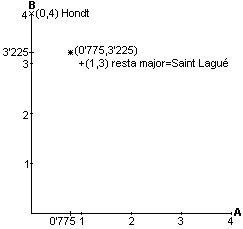
Per a distribuir 4 llocs entre 2 candidatures amb 31 i 129 vots respectivament:
Total
de vots a candidatures: 31+129=160
Candidatura A:
31 vots; proporció exacta: 4x31/100=0'775
Candidatura B: 129 vots;
proporció exacta: 4x129/100=3'225: punt (0'775,3'225)
Distribució per Resta
Major o Saint Lagué: 1 per a A i 3 per a B: punt (1,3). Veure Tabla
1.2.a
Distribució per Regla
d'Hondt: 0 per a A i 4 per a B: punt (0,4). Veure Tabla 1.2.b
|
|
|
2. Casos en que amb 2 vot menys la candidatura majoritària no obtindria cap lloc tampoc amb Resta Major i Saint Lagué:
2.1.
Per a distribuir 2 llocs entre 2 candidatures amb 26 i 74 vots respectivament:
Total de vots a candidatures:
26+74=100
Candidatura A: 26 vots;
proporció exacta: 2x26/100=0'52
Candidatura B: 74 vots;
proporció exacta: 2x74/100=1'48: punt (0'52,1'48)
Distribució per Resta
Major o Saint Lagué: 1 per a A i 1 per a B: punt (1,1). Veure Tabla
2.1.a
Distribució per Regla
d'Hondt: 0 per a A i 2 per a B: punt (0,2). Veure Tabla 2.1.b.
|
|
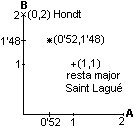
Figura 2.1 |
2.2.
Per a distribuir 4 llocs entre 2 candidatures amb 21 i 139 vots respectivament:
Total
de vots a candidatures: 21+139=160
Candidatura A:
21 vots; proporció exacta: 4x21/160=0'525
Candidatura B: 139 vots;
proporció exacta: 4x139/160=3'475:
punt (0'525,3'475)
Distribució per Resta
Major o Saint Lagué: 1 per a A i 3 per a B: punt (1,3). Veure Tabla
2.2.a
Distribució per Regla
d'Hondt: 0 per a A i 4 per a B: punt (0,4). Veure Tabla 2.2.b
|
|
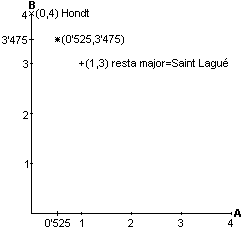
Figura 2.2 |
Es pot demostrar que amb 2 candidatures sempre s'arriba al mateix resultat: equivalència de Resta Major i Saint Lagué, i major aproximació a les proporcions exactes que amb la Regla d'Hondt sempre que aquesta done uns resultats diferents.
Rafael
Pla López
professor
Titular d'Universitat de Matemàtica Aplicada