Efficient Analysis and Synthesis using a New Factorization of
the Gabor Frame Matrix.
S. Moreno, F.J. Ferri, M. Arevalillo, W. Diaz
http://www.uv.es/prcv
Empirical validation
A comparative empirical assessment corresponding to the complete
computation of the DGE has been carried out. In particular, Gabor
coefficients are computed for audio signals of a given size using an
appropriate DGT algorithm using Nuttall windows of diferent sizes. Then, the signal is reconstructed with
negligible error using different DGE algorithms. The main goal is to
see to which extent theoretical flop counts correspond to empirically
measured CPU times and to identify which DGE algorithm is the best
option across a range of different parameters.
CPU measurements were obtained
by using an i7-based computer. All algorithms have been implemented in
plain matlab/octave, except the Factorization algorithm, that has been
taken from the LTFAT toolbox. The figures shown here correspond to the same experiments in the paper run in a different machine.
We first consider a non-painless Gabor system with M=60 channels, hop size a=30, and
Lg=120, as in Perraudin, 13.
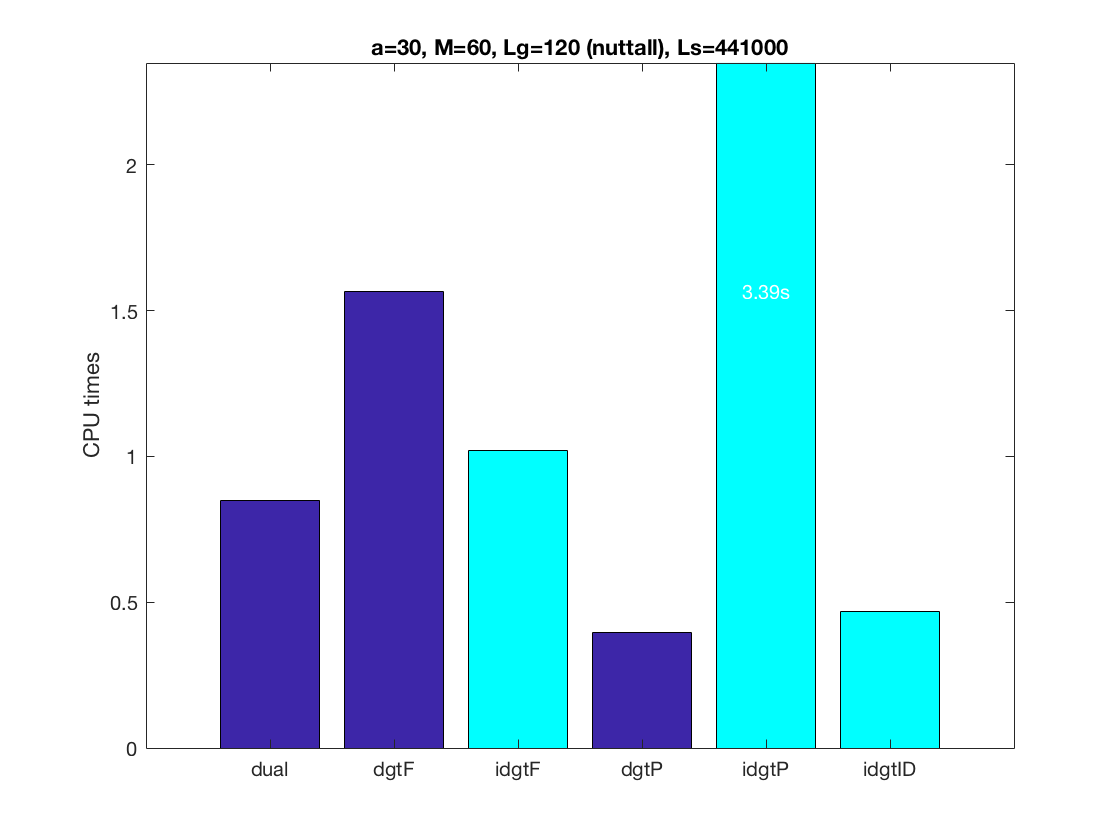
The bars in the first figure show the CPU times corresponding to
different options to compute the DGT/DGE along with the cost of
computing the canonical dual. The last bar (idgtID) corresponds to the
DGE proposal. Compare this CPU time against the Factorization algorithm
(idgtF) plus the dual cost (dual).
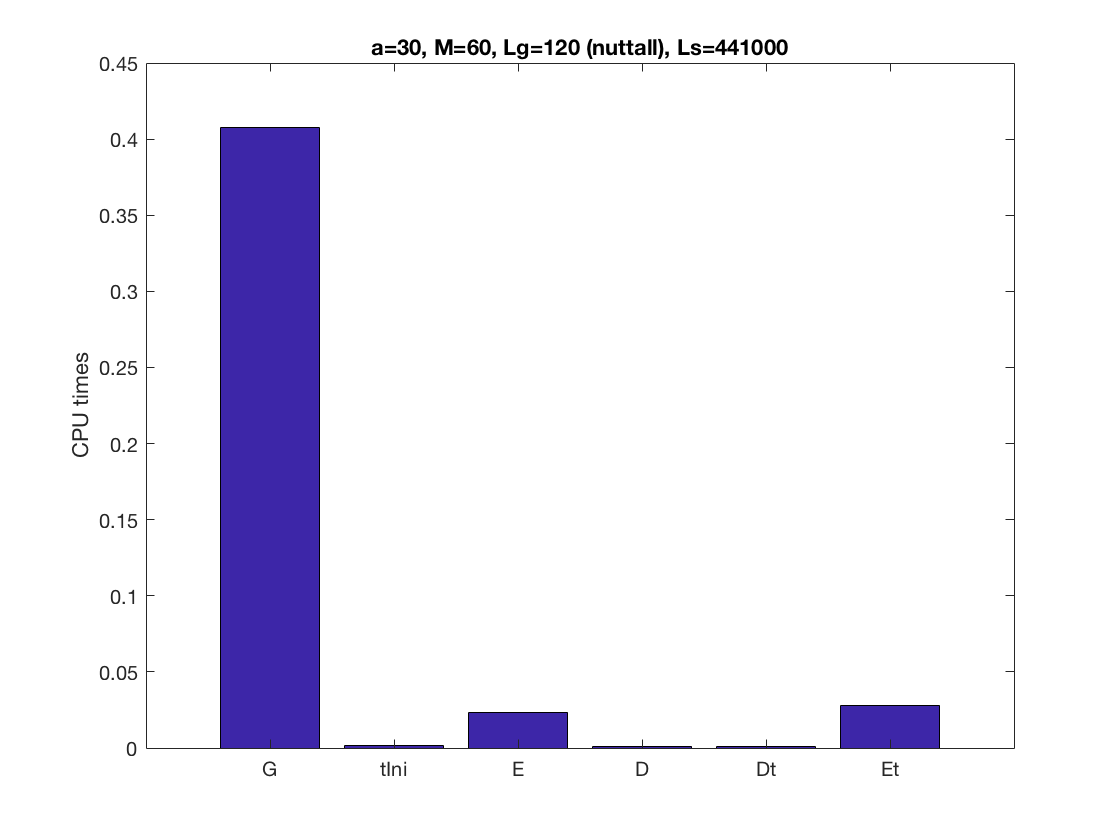
The bars in the second figure show the CPU times of the different steps
in the proposed algorithm. Note that most of the cost corresponds to
the "short DGE" step (G).
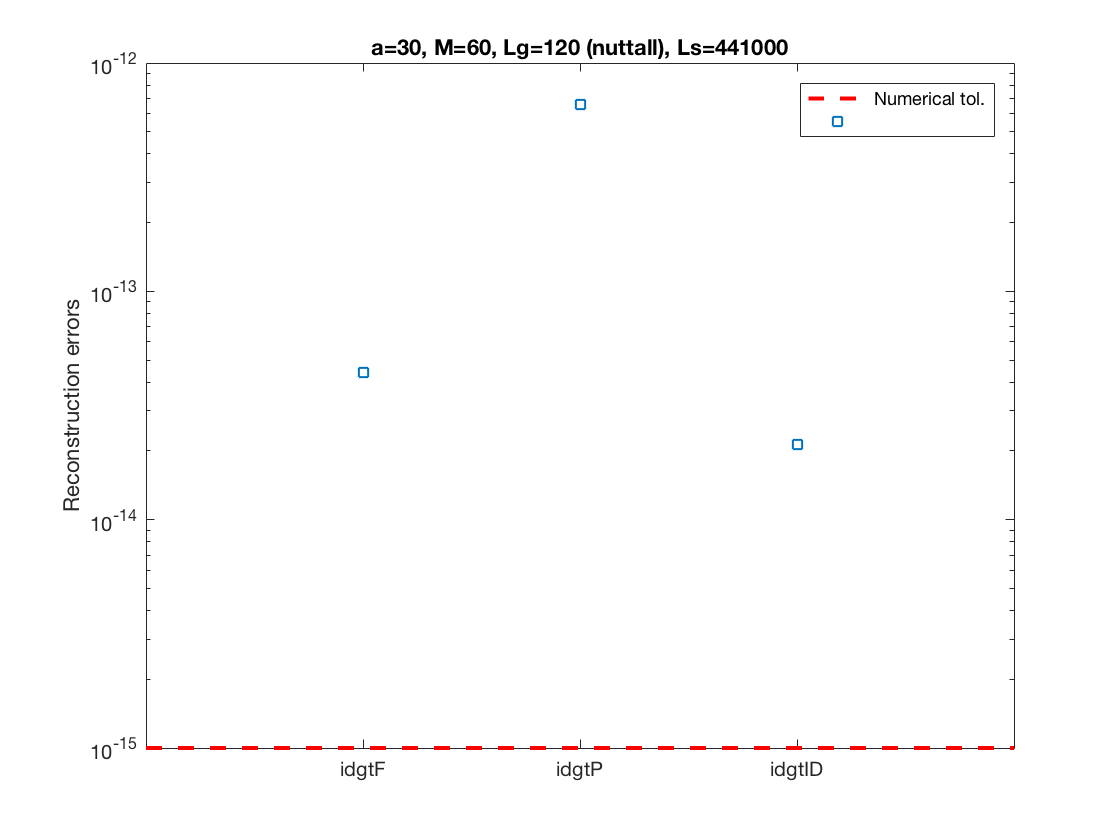
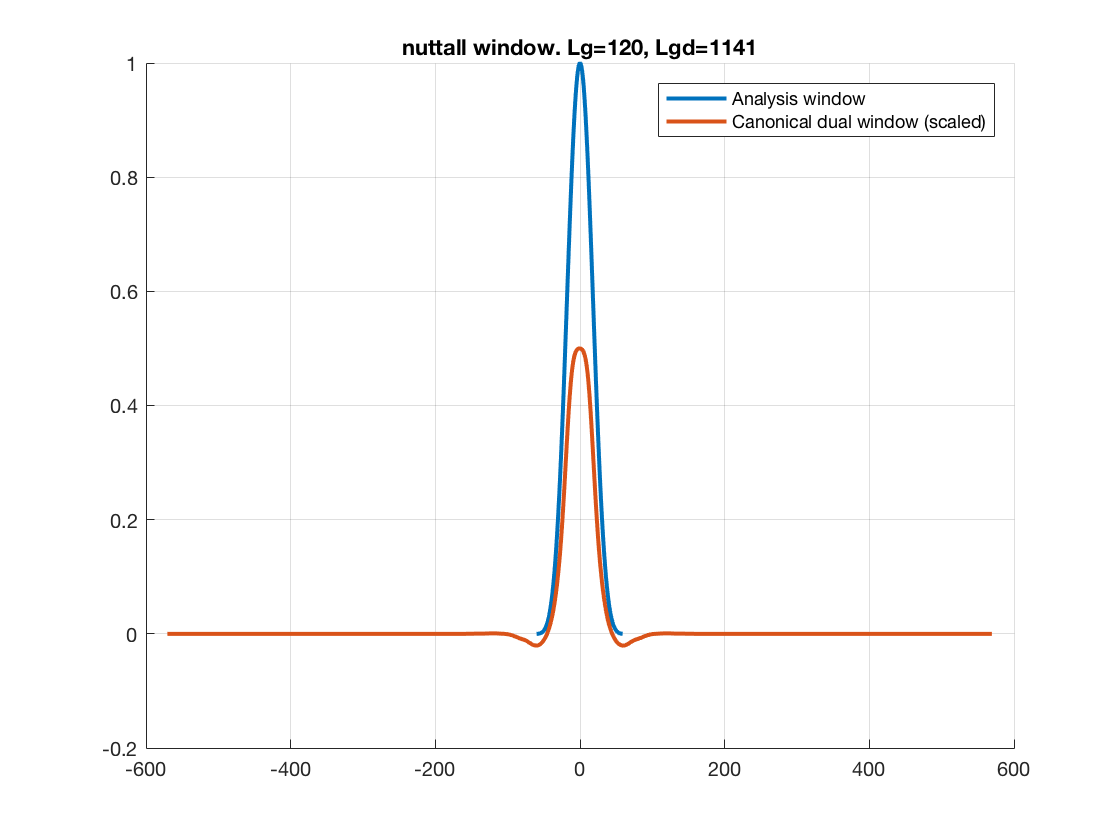
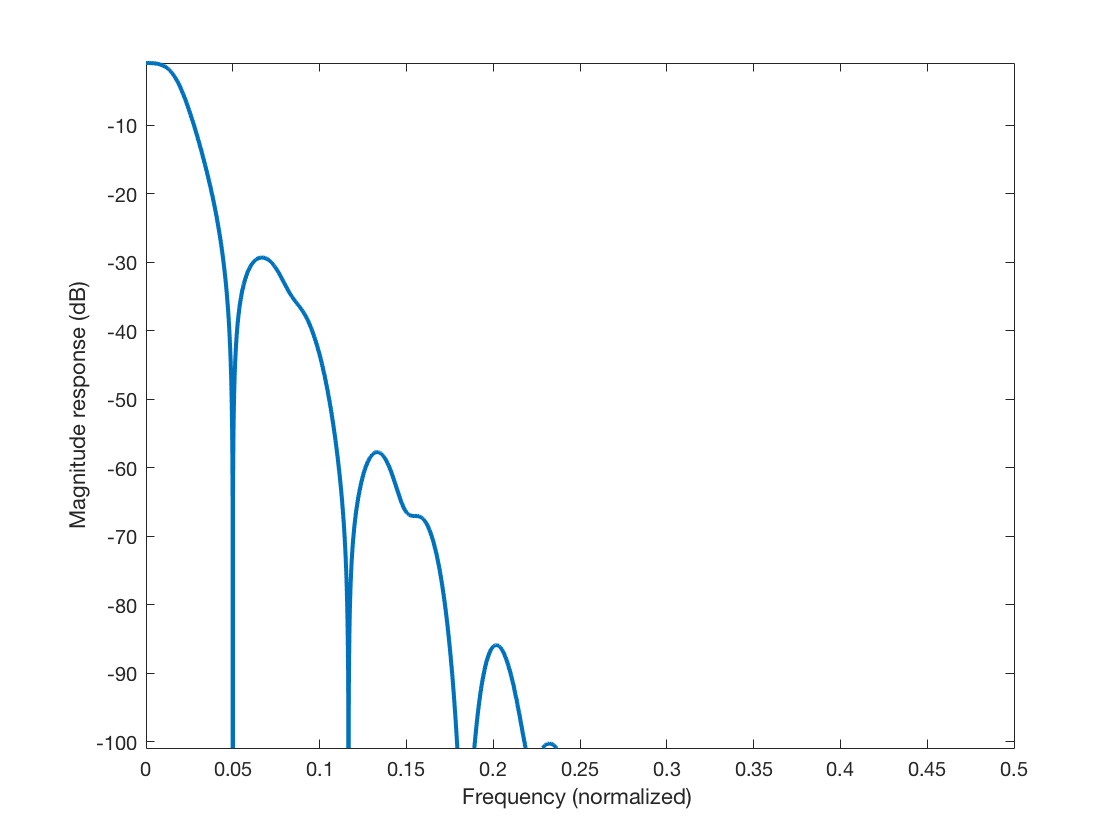
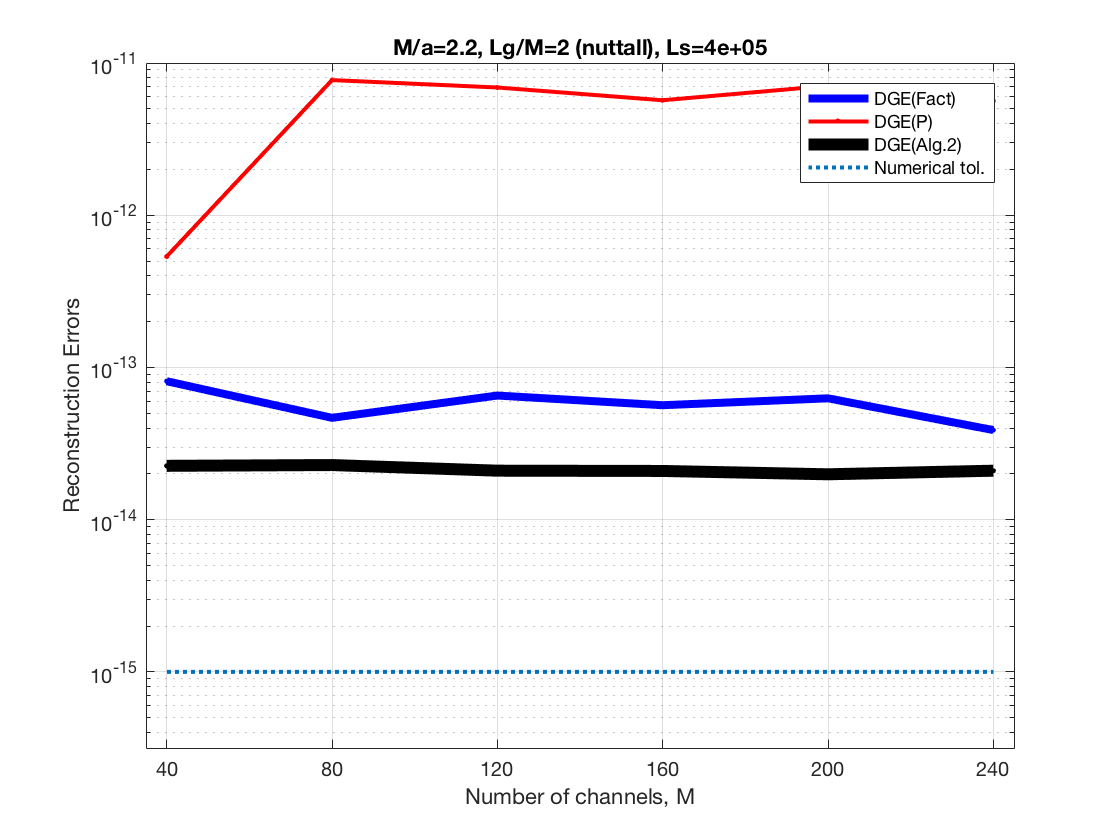
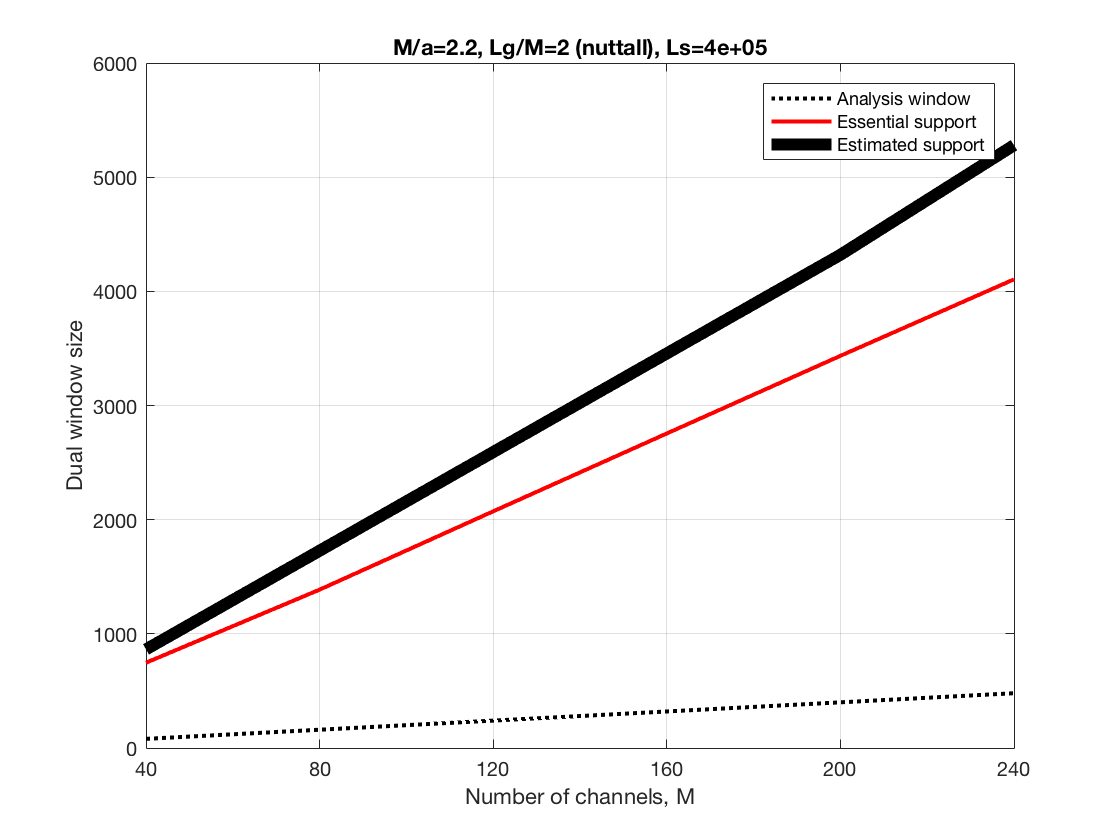
The last figures show reconstruction errors, the analysis and synthesis
(canonical dual) windows and the magnitude response in dB
corresponding to the synthesis window. Nothe that the Nuttall windows
used are nicely concentrated in frequency.
Alternative dual window with support Lg=120 obtained through convex optimization (Perraudin, 13)
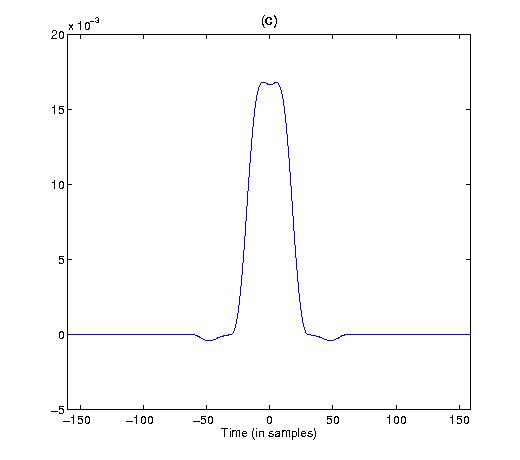
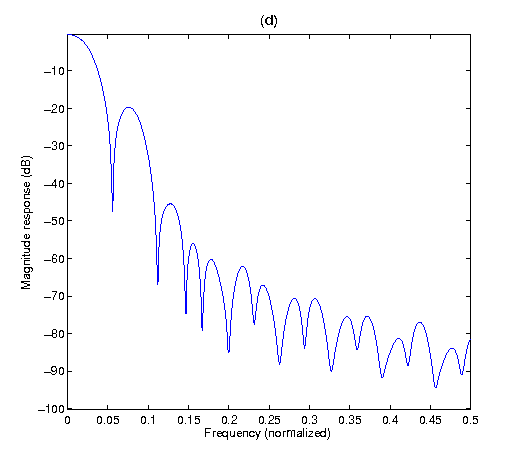
These figures show an alternative dual for the same Gabor system and its corresponding magnitude response.
The proposed algorithm allows using the
canonical dual of size Lg=1141, with much better concentration in
frequency, with only 10% more computational cost.
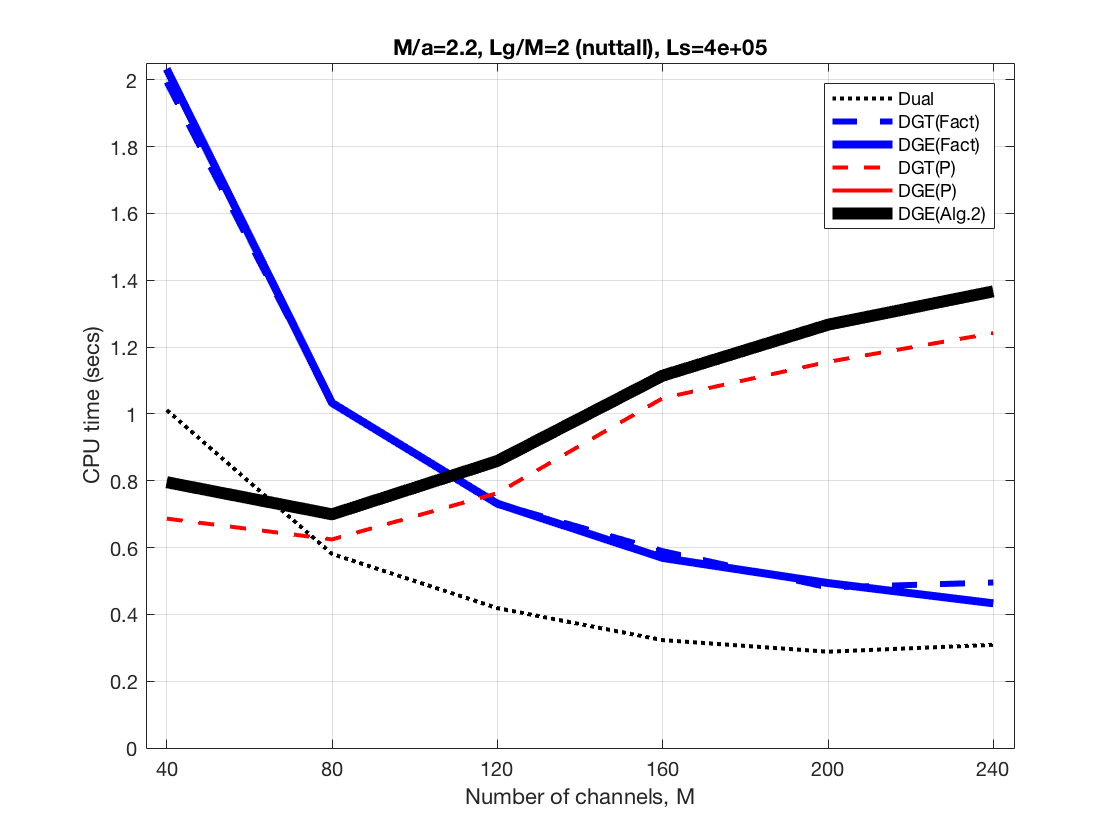
In the following and for each scenario we show CPU times, reconstruction errors, and essential support estimates
Increasing window size
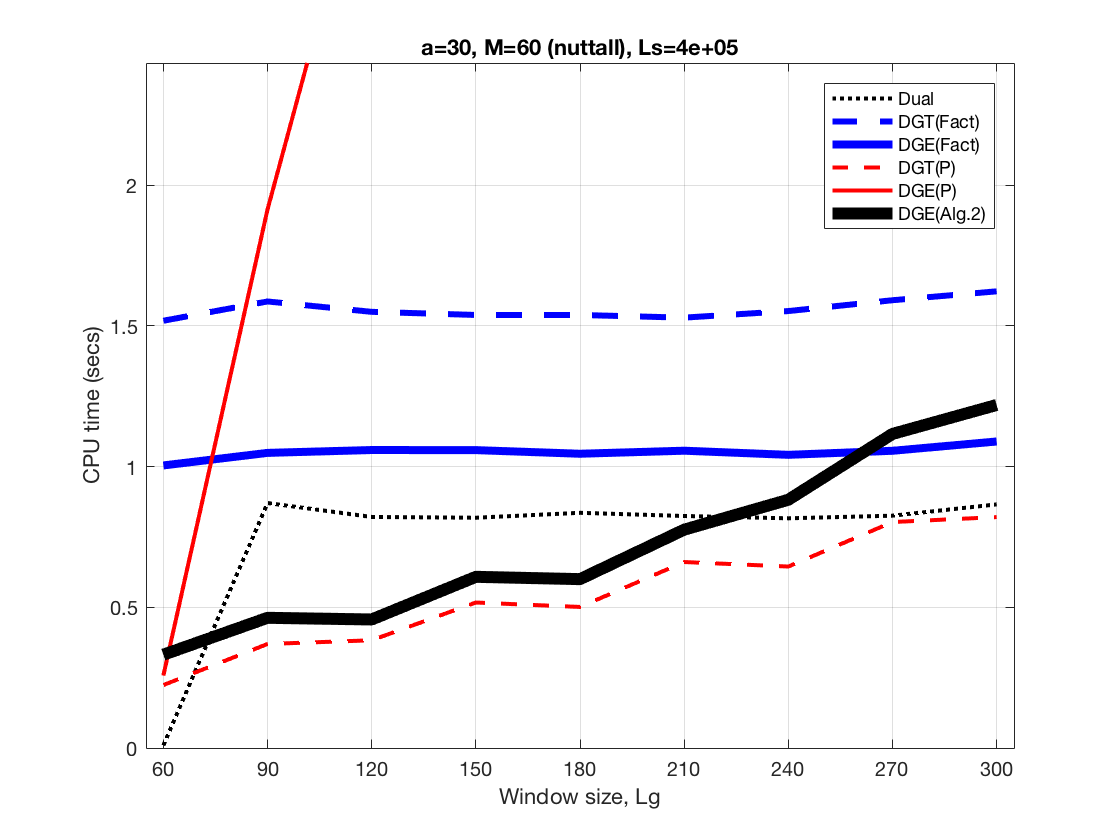
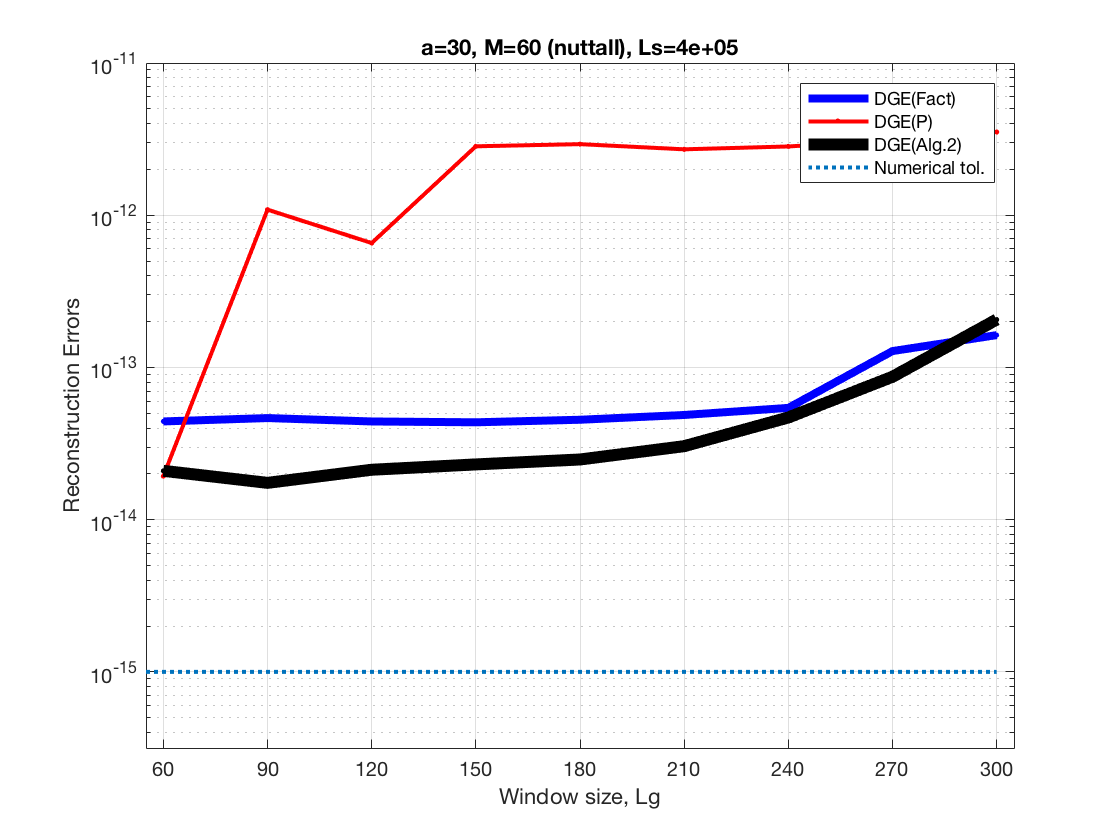
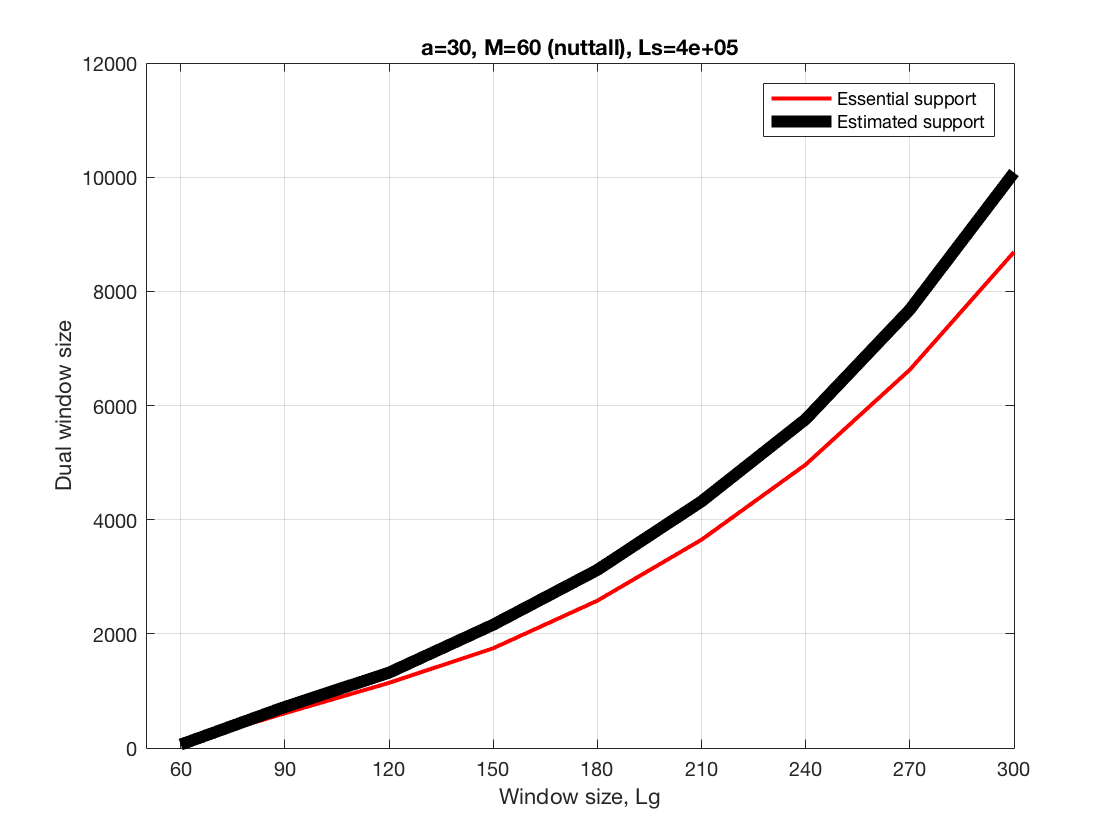
This shows the comparative behavior of the DGE algorithms as the size of the analysis window is increased
Increasing frequency channels at a constant ratio Lg/M
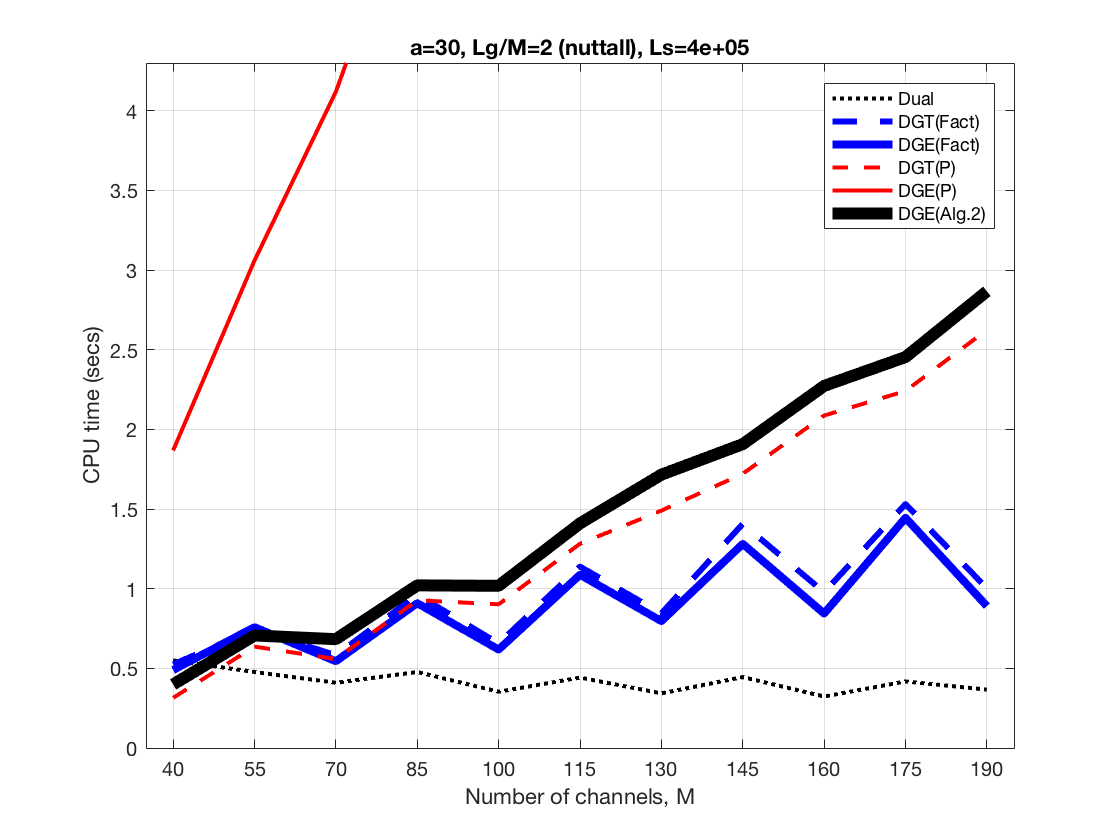
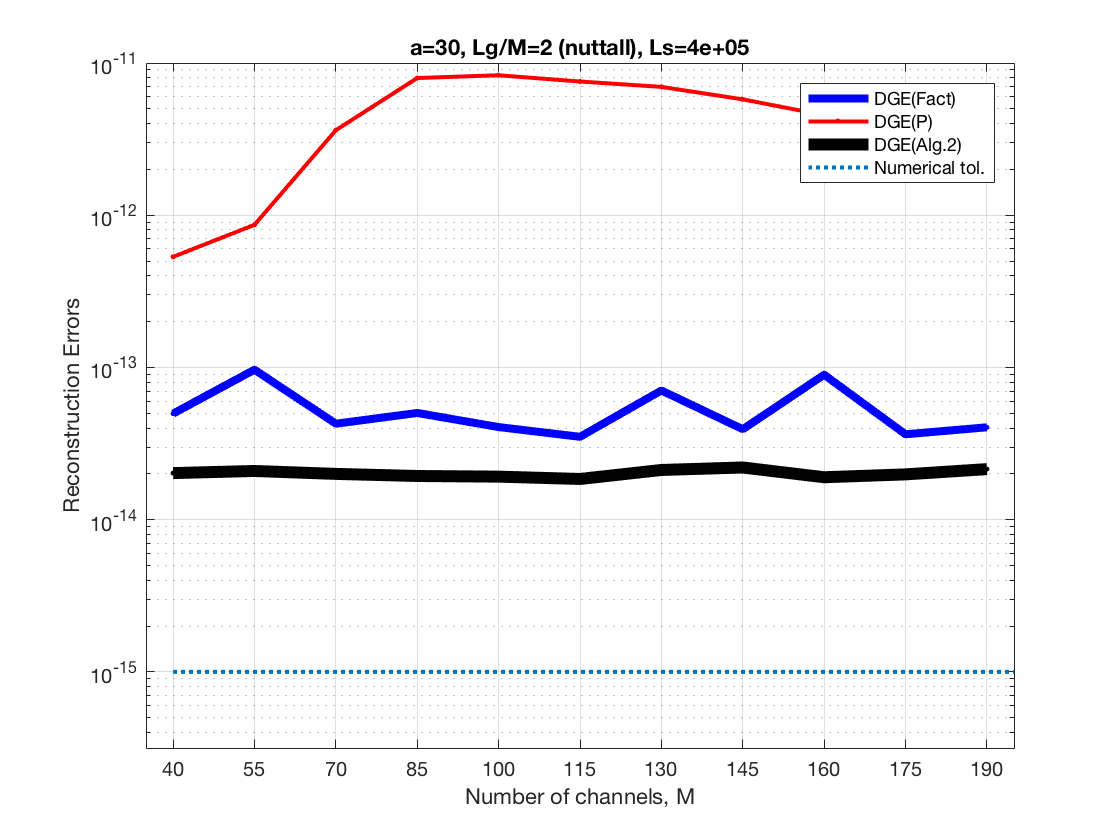
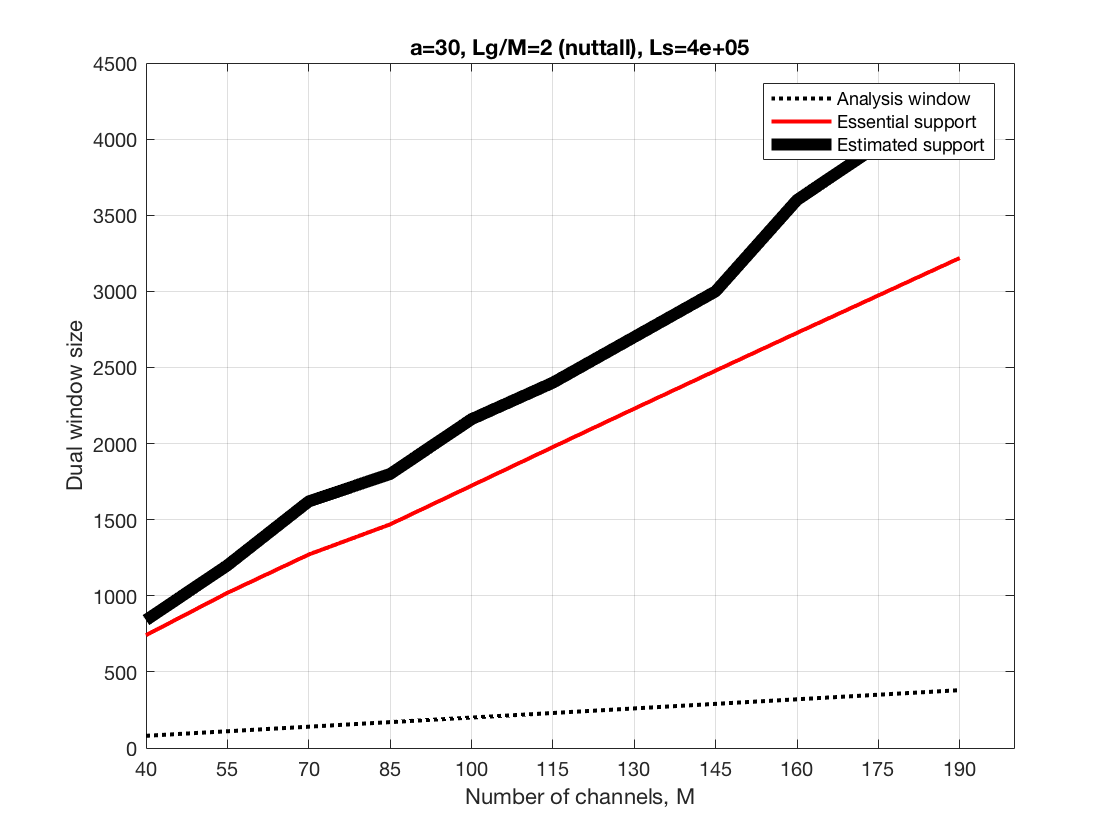
Now we increase the size of the synthesis window and the number of frequency channels at a constant ratio
Increasing frequency channels at constant Lg/M and constant redundancy, M/a=2
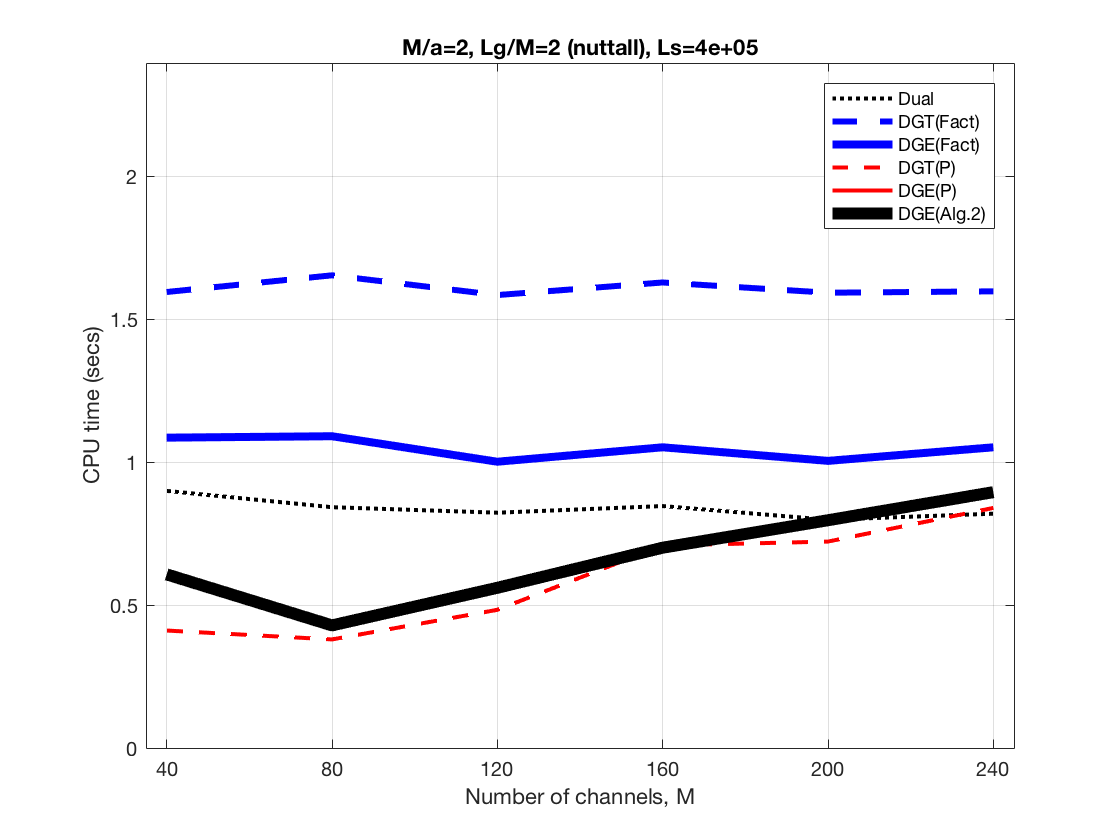
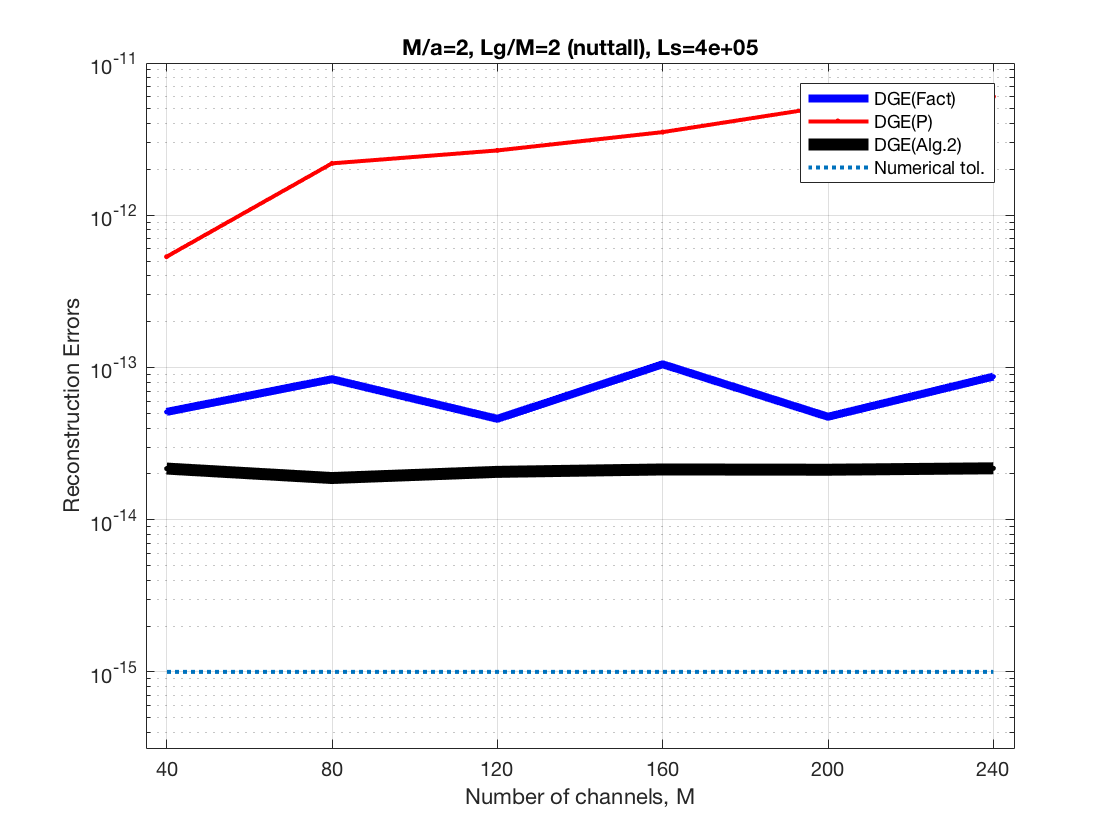
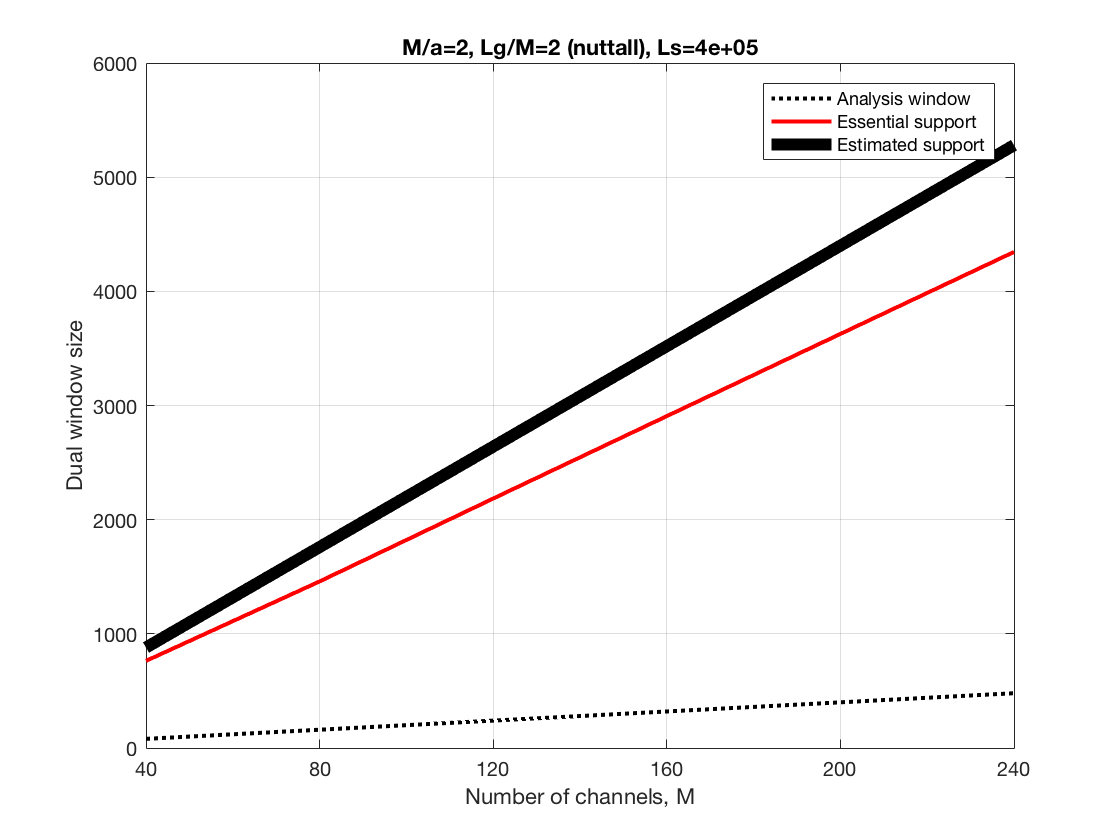
In some cases is interesting to fix a redundancy and increase M and Lg
and decrease timeshift, a. In the following we show the behavior of the
different DGE alternatives for M/a=2 and for M/a=2.2
Increasing frequency channels at constant Lg/M and constant redundancy, M/a=2.2
- -


















