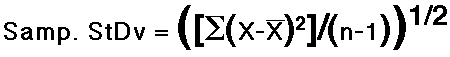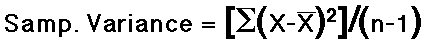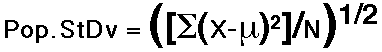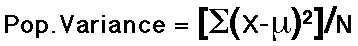Variability

Gravetter & Wallnau, Chapter 4; Young, Chapter 3

Copyright © 1997-8 by Forrest W. Young.

P30Home Schedule Labs Homework Project Lectures

  1. Overview

    2. Consider the four distributions obtained for variables in the survey done on the first day of class. The distributions are colored with red for males and blue for females:

    We can summarize these distributions by discussing their

    Central Tendency - Mean, Median, Mode
    Central tendency measures identify a single score as representative of an entire distribution of scores. The goal of central tendency is to find the single score that is most typical or most representative of the entire distribution.

    Variability - Standard Deviation, Variance, Range, IQ Range
    Variability measures provide a quantitative indication of the degree to which scores in a distribution are spread out or clustered together.

    Skewness - A measure of shape
    Skewness measures provide a quantitative indication of the degree to which scores in a distribution are located at one end of the distribution. Positive scores mean the distribution is positively skewed, and conversely.

    Kurtosis - Another measure of shape
    Kurtosis measures provide a quantitative indication of the degree to which scores in a distribution are peaked or flat. Positive values mean the distribution is peaked. Negative values mean the distribution is flat.

    The ViSta summary report presents measures of each of these characteristics of a variable's distribution. For these four variables, the report is:

  2. Three measures of variability

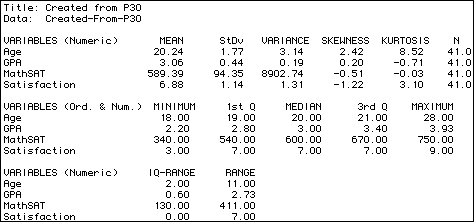
    1. The Range

      2. The range is the distance between the largest and smallest scores in a distribution. To determine the range, you must use the real limits of the maximum and minimum. This makes the formula for the range:

      range = URL(Max) - LRL(Min)

      where URL(Max) stands for "Upper Real Limit of the maximum score" and LRL(min)means the "Lower Real Limit of the minimum score".

      If the distribution consists of whole numbers (integers), the range is

      range (of integers) = Max - Min + 1

      Problem: Because the range doesn't consider all of the scores in the distribution, only the extremes, it often does not give an accurate description of the variability.

      ViSta's Range: ViSta calculates the range as simply

      range = Max - Min

      ViSta leaves off the term dealing with real limits. This is another way the range is commonly defined.

      Example:For the variables in our class data (see table above), the ranges are:


        Age: (28 - 18 + 1) = 11
        GPA: (3.93 - 2.20 + 1) = 2.73
        MathSAT: (750 - 340 + 1) = 411
        Satisfaction: (9 - 3 + 1) = 7

      Questions:

      1. How well does the range do as a way of representing the variation in each of these variables?
      2. Does it do better for some of the variables than for others?
      3. If so, why?

    2. The Interquartile Range and Semi-Interquartile Range

      3. We begin defining the interquartile range by first defining quartiles:

      Quartiles
      Quartiles are the percentiles at the locations which divide a distribution into quarters. There are three quartiles, denoted the first (Q1), second (Q2) and third (Q3):
      1. Q1 has 25% of the scores below it.
      2. Q2 has 50% of the scores below it (and, therefore, is the median).
      3. Q3 has 75% of the scores below it.

      Interquartile Range
      The interquartile range is the distance between the first and third quarters of the scores in a distribution. Thus, the formula is:

      IQR = Q3 - Q1

      Semi-Interquartile Range
      The semi-interquartile range is simply one-half of the interquartile range.

      SIQR = (Q3 - Q1) / 2

      Evaluation: The IQR and SIQR are more stable than the Range because they focus on the middle half of the scores and, therefore, can't be influenced by extreme scores. However, the actual value of the scores aren't used, which would be an improvement.

      Example:For the variables in our class data (see table above), the IQR values are:


        Age: (21 - 19) = 2
        GPA: (3.4 - 2.8) = 0.6
        MathSAT: (670 - 540 + 1) = 130
        Satisfaction: (7 - 7) = 0

      Questions:

      1. How well does the IQR do as a way of representing the variation in each of these variables?
      2. Does it do better for some of the variables than for others?
      3. If so, why?
      4. Do we get a different idea of variability in the data by looking at the IQRs than we did by looking at the ranges?

    3. The Standard Deviation and Variance

      4. Definition of Standard Deviation
      In simple terms, the standard deviation is the average distance of scores in a distribution from their mean.

      Definition of Variance
      The Variance is the square of the standard deviation.

      Examples
      Consider, once again, the four variables in our class survey data. Here are their means and standard deviations:

      1. Age: Mean = 20.24, StDv = 1.77

        One interprets the mean as showing that the typical age is about 20 1/4 years (20 years and 3 months). The standard deviation shows that the average person is within 1 3/4 years (1 year and 9 months) of that age. That is, most people in class are between 20.24-1.77= 18.47 (18 1/2 years old) and 20.24+1.77=22.01 years old (between 18 1/2 and 22).

      2. GPA: Mean = 3.06, StDv = .44

        The mean tells us that the average GPA is 3.06, corresponding to just above a B average. The standard deviation tells us that, on the average person has a GPA that is between 2.62 and 3.50. In other words, the typical GPA range is between a B- and B+/A-. Not bad!

      3. Math SAT: Mean = 589.39, StDv = 94.35

        The mean tells us that the average SAT score on the Math section is about 590 (which is certainly better than the average score in the whole population). The standard deviation tells us that, the typical person has a SAT score on the Math section that is between 495 and 685, or, roughly, between 500 and 700. This seems like a fairly big variation, suggesting that some students did quite a lot better than others on SAT Math.

      4. Satisfaction: Mean = 6.88, StDv = 1.14

        Typically, you rated your satisfaction with your experience at UNC averages about 7, which is above the middle of the scale (which was 5). Furthermore, most of you rated your experience in the 5 to 9 range, which is from the middle of the scale to the top of it. Its hard to know what this means, exactly, since we don't have a well defined reference for the scale, as we do for the other variables.

      Most Useful Measure of Variation
      The standard deviation and variance are the most useful measures of variation.

      Don't you feel as though you've learned more about the variability of the scores on the four variables discussed above than you did from the range or IQR?

      This is because it uses every score in the distribution to come up with a value for the variation in the scores, not just two scores (as for the range) or some of the scores (as for the IQR).

      Also, the standard deviation and variance are very much involved in inferential statistics, whereas the other measures are not involved.

      For these reasons, we will see these measures repeatedly throughout the book.

      The down side is that the formula is much more complicated than those for the range or IQR, as we will see next.

      Formula for the standard deviation
      The standard deviation is, roughly, the average difference of scores from their mean. More precisely, it is the square root of the "mean" of the squared difference of scores from their mean. Here is the formula:

      We see that:
      1. Square root: The standard deviation is the square root of everything inside, since the superscript of 1/2 means square root.

      2. "Mean" is modified slightly (and therefore I've put it in quotes) to involve dividing by n-1 rather than n, for reasons described in the "degrees of freedom" section of the chapter.

        This is true for the sample standard deviation (which is what we will almost always be computing), but not the population standard deviation (which we'll seldom see) where we divide by N, getting the true mean.

      3. Squared differences are used because the sum of the un-squared differences from the mean is always zero, which isn't useful for an index of variability! Always zero? Why is this?

        Note that here the differences are also distances. So we are figuring out how far the typical score is from the mean of the scores, in distances.

      Formula for the variance
      This is simply the square of the standard deviation:

      We will be using this formula in later portions of the book.

      Population Formulas
      The population formulas for the standard deviation and variance are the same, except they use the population mean (denoted by "mu" rather than "x-bar"), and they use the population size N, rather than 1 less than the sample size n. Here they are:

      Check out the HyperStat site. Pay particular attention to the first two chapters, especially the one on Describing Univariate Data.

      Use the Histogram Explorer to get a better understanding of histograms and distributions. Follow the Basic Instructions given there. Use the Practice Guessing.

      Also try this interactive demonstration of how to calculate the standard deviation and variance.