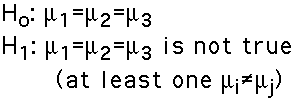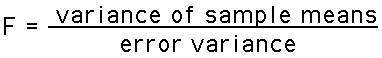Notes
Data
Applets
Examples

OnLine Help
New User
User's Guide
References

Notes on Topic 13:
One-Way Analysis of Variance

    One-Way ANOVA
    (Independent-Measures)

     

    Example:

    This is hypothetical data from an experiment examining learning performance under three temperature conditions. There are three separate samples, with n=5 in each sample. These samples are from three different populations of learning under the three different temperatures. The dependent variable is the number of problems solved correctly.

    Independent Variable:
    Temperature (Farenheit)
    Treatment 1
    50-F    		 Treatment 2
    70-F    		 Treatment 3
    90-F
    0
    1
    3
    1
    0    		 4
    3
    6
    3
    4    		 1
    2
    2
    0
    0
    Mean=1 Mean=4 Mean=1

    This is a one-way, independent-measures design. It is called "one-way" ("single-factor") because "Temperature" is the only one independent (classification) variable. It is called "independent-measures" because the measures that form the data (the observed values on the number of problems solved correctly) are all independent of each other --- they are obtained from seperate subjects.

    Hypotheses:

    In ANOVA we wish to determine whether the classification (independent) variable affects what we observe on the response (dependent) variable. In the example, we wish to determine whether Temperature affects Learning.

    In statistical terms, we want to decide between two hypotheses: the null hypothesis (Ho), which says there is no effect, and the alternative hypothesis (H1) which says that there is an effect.

    In symbols:

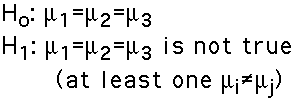
    Note that this is a non-directional test. There is no equivalent to the directional (one-tailed) T-Test.

    The t test statistic for two-groups:

    Recall the generic formula for the T-Test:

    For two groups the sample statistic is the difference between the two sample means, and in the two-tail test the population parameter is zero. So, the generic formula for the two-group, two-tailed t-test can be stated as:

    (We usually refer to the estimated standard error as, simply, the standard error).

    The F test statistic for ANOVA:

    The F test statistic is used for ANOVA. It is very similar to the two-group, two-tailed T-test. The F-ratio has the following structure:

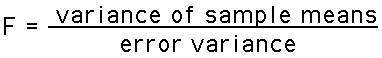
    Note that the F-ratio is based on variance rather than difference.

    But variance is difference: It is the average of the differences of a set of values from their mean.

    The F-ratio uses variance because ANOVA can have many samples of data, not just two as in T-Tests. Using the variance lets us look at the differences that exist between all of the many samples.

  1. The numerator: The numerator (top) of the F-ratio uses the variance between the sample means. If the sample means are all clustered close to each other (small differences), then their variance will be small. If they are spread out over a wider range (bigger differences) their variance will be larger. So the variance of the sample means measures the differences between the sample means.

  2. The denominator: The denominator (bottom) of the F-ratio uses the error variance, which is the estimate of the variance expected by chance. The error variance is just the square of the standard error. Thus, rather than using the standard deviation of the error, we use the variance of the error. We do this so that the denominator is in the same units as the numerator.