a) Supuestos:

Los datos son independientes.

b) Hipótesis:

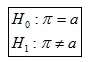
c) Estadístico de contraste:

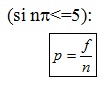
Muestras grandes

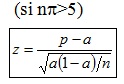
d) Distribución del estadístico de contraste:

Si la muestra es pequeña, el estadístico de contraste p sigue la distribución Binomial. Si la muestra es grande, z sigue la distribución Normal estandarizada:

e) Significación del estadístico de contraste.

g) Intervalo de confianza:

 

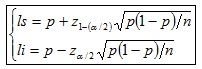
Ejemplo

Queremos probar si una moneda de un Euro está bien construida en el sentido de que la probabilidad de "cara" es la misma que la de "cruz", por lo que lanzamos la moneda 20 veces y observamos 8 "caras". Es razonable pensar que la moneda está bien hecha? (alfa=0.01).

a) Supuestos: Dado que los datos venden de lanzar la moneda al aire, es razonable suponer que son independientes.

b) Hipótesis:

Asignamos 0.5 al parámetro porque inicialmente pensamos que la moneda está bien hecha.

c) Estadístico de contraste:

Muestras grandes:

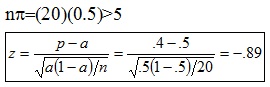
Se asigna 0.4 a "p" porque 8 caras de 20 es una proporción igual a 0.4

d) Distribución del estadístico de contraste: Normal.

e) Significación del estadístico de contraste: 0.19

f) Decisión: Dado que este valor es superior al nivel de significación (0.01), aceptamos la Hipótesis Nula.

g) Intervalo de confianza:

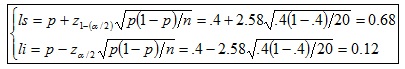
Diremos con un nivel de confianza del 1% que la verdadera proporción de caras de la moneda de la prueba está entre 0.68 y 0.12

Conclusión: La evidencia obtenida no hace pensar que la moneda esté mal hecha.