Búsqueda binaria
Complejidad de algoritmos
Complejidad de algoritmos

Problema: nos dan una lista de n números y nos piden buscar dos de ellos que cumplan una condición.
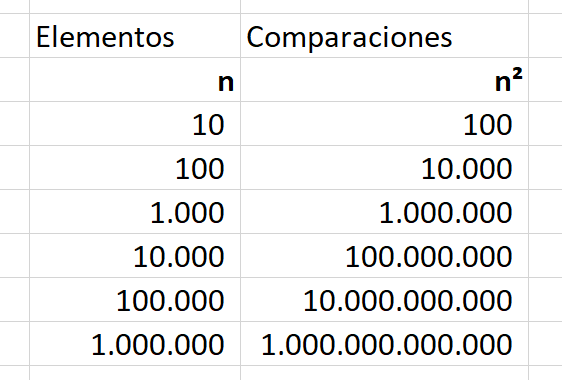
Si los comparamos todos con todos acabaremos haciendo unas n*n comparaciones.
Si n=1.000 se hará un millón de operaciones, si n=10.000 se harán cien millones de operaciones
Crecimiento cuadrático n*n
Como se ve conforme aumenta el número de elementos las comparaciones a realizar se disparan.
Código
Haciéndolo así, por fuerza bruta, el código sería más o menos este

Inviable
Como se ve la complejidad es O(n²), hay que reducirla a algo que no sea cuadrático.
Solución
Ordenar los datos y usar una búsqueda binaria.
Búsqueda binaria
La búsqueda binaria permite que, si los datos están ordenados, no haga falta comparar con todos los de la lista.
Primero iremos a mitad de la lista, y si el elemento es menor que el deseado ya no hará falta comparar con ninguno de la primera mitad.
Haciendo eso repetidas veces al final en vez de hacer n comparaciones se harán solo log₂n.
Complejidad total
Para comparar todos los elementos (N) con los otros mediante búsqueda binaria la complejidad resultante es n*log₂n.

Crecimiento logarítmico
Como se ve la subida es mucho menos acusada, ahora sí es asumible el costo.
Código
El código quedaría así

Resumen
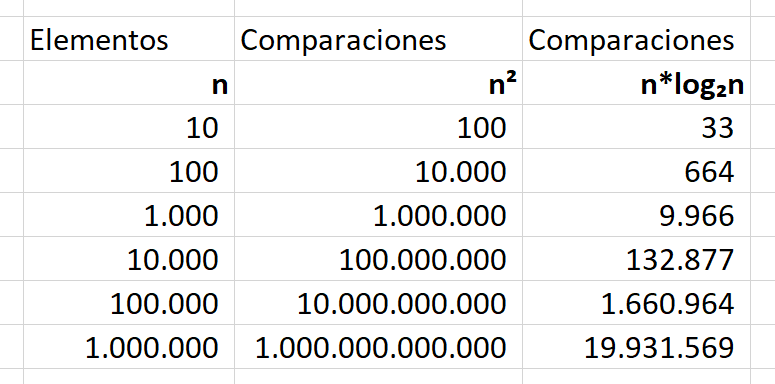
El número de operaciones es muchisimo menor. Para diez mil elementos
n = 10.000
Por fuerza bruta habríamos hecho cien millones de operaciones.
O(n²) → 100.000.000
Con la búsqueda binaria se reducen a 133.000.
O(n*log₂n) → 132.877
Conclusión
El costo de ordenar al principio la lista de números y hacer luego la búsqueda binaria se compensa con creces al reducir el número total de operaciones.
Contacto
¿Quieres contactar conmigo?
@xblasco.com (blueSky)