Economical consequences from a model of social evolution.
Vicent Castellar-Busó & Rafael Pla-López
Departament de Matemŕtica Aplicada
Universitat de Valčncia
|
Abstract In this work we modelize, with an abstract mathematical model by computer simulation, the interaction between the social behaviours and a common ecological environment. The social systems consume resources to satisfy their needs or to repress other behaviours. There is a bound for the sustainable consumption: if this is not surpassed, the consumed resources are recovered without cost (natural cycles, reutilization...). After surpassing it, the recovery has a cost in recycling and the ecological degradation implies the decrease of the satisfaction. Our model studies the transition conditions toward an ecological balance or the destruction of the environment. |
Introduction: the model.
We work with an Adaptive, Historical, Geographical and Multidimensional Model with Resignation [1, 2, 3, 4] built from a General Learning Theory [5] which is formulated in terms of General Systems Theory [6]. By means of this Mathematical Model, we have studied the possible paths of evolution from a Full Repressive Society to a Free Scientific Society with a multidimensional state-variable which values characterise social behaviours.
The Model is composed by means of the interaction of several mathematical Systems, which express the relations between the variables involved:
The core of the Model is the Learning System, through positive and negative reinforcement: the probability (P) of each social behaviour (U), in each individual subsystem (N) of a social population, increases when his goal is fulfilled and decreases when it is not fulfilled from this social behaviour. If no social behaviour available to an individual subsystem produces goal fulfilment, then this subsystem can be destroyed. The fulfilment probability (PG) depends on its technical possibility (p), which is weighted by a factor determined by the social organisation (1 – s).
This factor is generated by a Repression System: each social behaviour, according to its scope (F) in each individual subsystem, the impact (I) of this on different individual subsystems, and its repressive capacity (k), produces a decrease of this factor for the different social behaviours. Thus, each social behaviour represses the other social behaviours, by decreasing its goal fulfilment.
A Relay System produces a random (a) substitution (g) of an individual subsystem for a "child subsystem" with initial equiprobability (natalis) of every available social behaviour. A "child subsystem" can also occupy (A) the niche of a destroyed subsystem. Thus, relay causes the loss of the information accumulated in the substituted individual subsystem.
Also, a Science System determines the probability of learning (PL) for each social behaviour in each subsystem: the probability of the experience of other subsystems, which is weighted by factors of emission, reception and impact, is added to its own experience. This System expresses the relations of intellectual communication between different individual subsystems.
A Historic System simulates historical evolution through the random (b) increase (d) of the dimension (m) of the state-variable in each subsystem, and therefore of the number of its available social behaviours. The probability of evolution is increased (b) by the existence of social behaviours, which were theoretically not available but are forced by the Science System from the experience of other subsystems. This System expresses technological progress and technological diffusion (we characterise a technologically higher society by a greater capacity of choice between different social behaviours).
An Adaptive System determines the dynamic evolution (Ta) of the repressive capacity in a subsystem, from an initial value (k) -when it is a "child subsystem"- which depends on the might (m), associated to the technological level, and on the ferocity (g) of the social behaviour, toward its suffered repression (s). The Adaptation Time Ta expresses the delay in the adaptation of produced repression (s) to suffered repression (s). Thus, with a low delay Ta, the produced repression equals quickly the suffered repression. On the contrary, with a high delay Ta, produced repression remains approximately constant.
A Resignation System expresses the influence of subjective factors through a tendency to a statistical normalisation of the reinforcement from satisfaction and dissatisfaction. We name this tendency "resignation", and express it by a time of delay (Tr) according to a model of Systems Dynamics.
Moreover, a Delay System expresses the decrease of Adaptation Time Ta with might µ, the increase of Resignation Time Tr with ferocity n, by means of the parameters Ka and Kr respectively. Moreover, Time Te increases with ferocity and decrease with might by means of a parameter Ke. An Impact System expresses how the impact I on repression and intellectual communication depends on might m and distance (d) between subsystems.
A Natural System expresses a diversity of initial condition natalis of the individual subsystems.
Economical factors: recycling, reutilization and ecology.
Now, we will use an Ecological System to represent the degradation of the environment as a consequence of the consumption in satisfaction and repression: the possibility of consumption decreases, so much in satisfaction like in repression, in order to recover the environment by means of the recycling.
We will represent the ecology by means of a global variable E not negative. This variable will begin from an initial value E0 sufficiently elevated like so that it were possible to be kept a consumption in satisfaction or in repression, during all the evolution, as high as the whole of the active systems could sustain. Moreover, the sum of this consumption during all the evolution can amount to the maximal level simultaneously, but they won’t remain thus by cause of the degradation that the environment would suffer. This variable can reach the value zero, situation that we will name ecological hecatomb. A value that permits this situation is E0 = 2NP.
The consumption in satisfaction and in repression contributes to the decrease of the resources. It is necessary define and characterise the processes by means of which it is also possible the increase of this variable, always between their extremes. These processes are the reutilization and the recycling.
The difference between reutilization and recycling will be that the first didn’t include a cost which will characterise the second. This cost produces a decrease in the consumption in satisfaction, in repression or in both. Really, we could assimilate the cost of the reutilization into the recycling and associate the reutilization to natural cycles and crops. We will name r to the reutilization and r to the recycling.
The expressions of the consumption in satisfaction, the consumption in repression and the cost of recycling are respectively
K2 = SN,U s(U,N)P(U|N) and
K3 = SN,U r(U,N)P(U|N).
The effects of the consumption on the ecology are global, so that the influence on the environment acquires the same form for any social behaviour in any system.
The reutilization is associated to natural cycles, so it is bounded by the half of the available resources7. We also considered that it is bounded by the consumption in satisfaction and repression and it could not be negative. The expression r = max[0, min[˝E, E0 – E + K1 + K2]] give us the value of the reutilization.
The recycling is formulated concerning an ideal value, which it corresponds to the consumed and not reutilized resources and it could not be negative. So, we express the ideal recycling by means of rI = max[0, min[E0 – E – r + K1 + K2, E0].
We will apply a retard
![]()
where Ke is a parameter that can vary in a set of initial conditions.
Finally, we also consider that the maximal possible cost in recycling which corresponds to each social component is bounded by their possibilities of consumption.
So
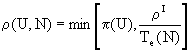
and
Also, the relationships with the environment modify the satisfaction PG(U;N) for each social behaviour in each system, by increasing with the recovery of the environment but decreasing with the cost of the produced recycling, according to
![]()
We have implemented our model in language C and executed it on the IBM 9021/500 of the SIUV (Servei Informŕtic de la Universitat de Valčncia) for the set of initial conditions (Ka,Kr,Ke) Î {1,4,..,97}x{1,4,..,97}x{1,2..10}. We work with NP = 40 individual subsystems, a maximum dimension mmax = 4 and binary components Ui Î {0,1} of the social behaviour U.
With this specification, U = (0000) would correspond to a Primitive Society with a technical possibility of satisfaction equal to 0, without scientific communication, and which has ferocity but not might, and therefore has no repressive capacity.
In the same way, U = (0111) = 7 can correspond to a Full Repressive Society with technical possibility of satisfaction p = ľ, some scientific communication and full repressive capacity k = 1.
Finally, U = (1111) = 15 = F corresponds to a Free Scientific Society with full technical possibility of satisfaction p = 1, full scientific communication and null repressive capacity k = 0.
We speak about predominance of a behaviour U if its probability is the majority (P > ˝) in a relative majority of subsystems. Moreover, we speak about strong predominance if additionally its probability of satisfaction (PG) is the maximum.
In prior works, we have studied [1, 2, 3, 4 , 5, 7] the social evolution from a Primitive Society with different values of the parameters. In the present work we are going to study the economical evolution, that is to say, the evolution of the resources, the consumption, the satisfaction and the might.
Evolution of consumption during the absence of bounds effect.
The exponential growth is a common characteristic to the not bounded models. Therefore, we wait that it also occurred in our model during the absence of bounds effect. This absence doesn’t only mean that the consumption had not reached its limit: during the temporal interval in which the resources have not decreased, the evolution is equivalent to an evolution without bounds for the consumption, because all the consumed resources have been recovered spontaneously, without cost, by reutilization. We will name tEo to the instant in which the bounds are reached.
In the initial phase, the predominant behaviours are characterised by a small variation of the values of the technical possibility of satisfaction, which limits the consumption. We will name t0 to the instant in which it concludes the effect of this limit.
We have taken the values of each evolution during the intervals in which the bounds don’t affect to the development, and we have fit the consumption to functions of the form K(t) = eat + b. Moreover, we have observed that the transformation
![]()
and the expression K(t) = eat’ + b proportions better fittings which are independent of the parameters Ka, Kr and Ke.
The calculations proportion the functions
![]()
and
![]()
for the consumption in satisfaction and for the consumption in repression respectively. The coefficients of correlation are r1 = 0’991 and r2 = 0’988 respectively. The average period is T = 4.672.
The solution of the equation K1(t) = K2(t) proportions gives t0 @ tEo. In the instant tEo the consumption in satisfaction and the consumption in repression have approximately the same value.
The sum of both consumptions is C(tEo) @ C(t0) = K1(t0) + K2(t0) @ NP = ˝E0.
Variation of the consumption in repression after reaching the sustainable bound.
We have seen that, near the instant tEo, the consumption in satisfaction and the consumption in repression coincide and its sum reaches the sustainable bound. In this instant, the consumption in repression finishes the exponential growth and acquires a lineal variation during an interval of significant time. We name tr to the extreme superior.
Then, we will represent the evolution of the consumption by the lineal model
![]()
for r = 0’974.
By fitting the consumption in repression in this instant, we obtain
K2(tr)= 2’314ln(Ka) – 0’365E(tr) + 21’656 for R = 0’832
We summarised the relationship between ecology and repression in the table
Ecological hecatomb |
Absence of ecological hecatomb |
|
K2(tr) < ˝NP |
6’76% |
12’35% |
K2(tr) ł ˝NP |
60’30% |
20’59% |
Evolution of the satisfaction during the absence of bounds effect.
We have modelized the satisfaction growth in a similar way that the consumption in repression during this period, by means of a lineal model with
![]()
The coefficient of correlation is r = 0’981. Moreover, the coefficient is independent of the parameters Ka, Kr and Ke.
Might Growth.
The characteristics of the growth of this function are:
- The might is zero in the initial instant.
- The rate of the growth begins with a null value, it increases until reach the maximum and it decreases until reach the zero again.
After considering functions that complete these properties, in particular the logistic function, the better option that we have found to model the growth of the might (m) is the function
![]()
Now we should find the interval during which the model is valid, the value of the maximal amplitude A and the value of the half-period t.
The transition from a Full Repressive Society to a Free Scientific Society permits that the might change suddenly: thus, the instant of its appearing, that we will name tFSS, is a superior bound of the valid interval.
E < E0 from the instant tEo. For this reason, we propose that tEo is the point of inflection of the growth. Therefore, we will take the half-period t = 2tEo. In addition, 2tEo is also a superior bound of the valid interval in order to explain the growth. We will call tf = min[2tEo, tf, tFSS] and we will take the interval [0, tf].
Finally, we will take the amplitude A = ![]() in each trajectory.
With these considerations, we get the function
in each trajectory.
With these considerations, we get the function
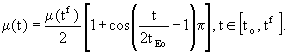
This model is independent of the parameters Ka, Kr and Ke. The influence of the parameters is included in tEo. The coefficient of correlation is r = 0’992.
Conclusions
According to our model, the growth of the consumption presents an short initial phase in which doesn’t admit a exponential model because of the inability of the systems in order to maintain it. Soon this ability is reached and the consumption grows exponentially until reaching the sustainable bound. In this instant, the consumption in repression overcomes the consumption in satisfaction. Later, the consumption in satisfaction evolves irregularly, while the consumption in repression evolves lineally. This fact is very interesting because in some studies8, that consider a finite quantity of resources, the exponential growth is immediately and necessarily followed by a collapse. Our model presents a phase in which the consumption could be ecologically adapted to the quantity of available resources.
Also, we can modelize the growth of the might by means of the growing portion of a cosine, which expresses the inflection and the limit of this growth.
In sum, our model follows the trend that considers the limits of the growth, but includes inside the self-model the option between the hecatomb and the survival through an adaptive process of recycling.
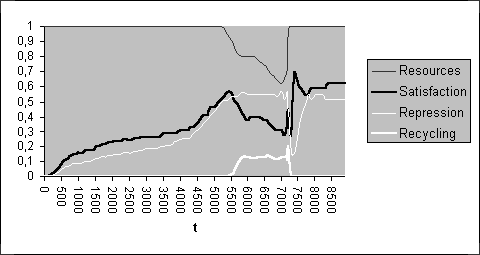
Evolution of the consumption and the
resources without hecatomb
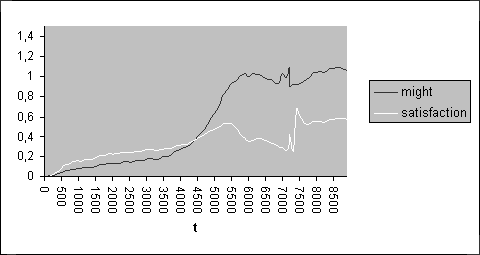
Evolution of the might and the
satisfaction without hecatomb
Bibliography
R. Pla-López, "Model of Multidimensional Historical Evolution", in R. Trappl ed, Cybernetics and Systems’90, World Scientific, Singapore, 575-582 (1990).
R. Pla-López, "Model of Adaptive, Historical and Multidimensional Social Learning", in R. Trappl ed, Cybernetics and Systems Research’92, World Scientific, Singapore, 1005-1012 (1992).
R. Pla-López, "The Role of Subjective Factor in Social Evolution", Second European Congress on Systems Science, Prague (1993).
R. Pla-López and V.Castellar-Busó, "Model of Historical-Geographical Evolution", in R. Trappl ed., Cybernetics and Systems’94, World Scientific, Singapore, vol. I, 1049-1056 (1994).
R. Pla-López, "Introduction to a Learning General Theory", Cybernetics and Systems: An International Journal 19, 411-429 (1988).
G.J. Klir, "An Approach to General Systems Theory", D. Van Nostrand Co., London (1969).
V.Castellar-Busó and R. Pla-López, "A Model of Sustainable Development Opposite to the Ecological Destruction", 14th International Conference of WACRA-Europe on Sustainable Development, Madrid (1997)
D. H. Meadows, D. L. Meadows and J. Randers, "Beyond the Limits", Doubleday Press, New York (1992).