Models of Dual Social Evolution
Rafael Pla-López
& Vicent Castellar-Busó
Departament de Matemàtica Aplicada
Universitat de València
Introduction.
The usual global models of the world [1] work essentially through extrapolations from the present world, without considering changes of behaviour nor social transformations. On the contrary, we are interested in modelling social evolution with qualitative changes: these processes cannot be avoided to study long ages of the history of the humanity, and we want to modelize the whole history of the whole humanity.
Thus, we have developed in prior works different mathematical models of social evolution, [2, 3, 4] in order to modelize that evolution through different phases.
We have modelized the social evolution by the way of an interaction by all of a certain population of individual subsystems NP through repressive action and scientific communication.
We have characterized the social behaviours of a social system by the probabilistic distribution of the values of a binary multidimensional variable U, and modelize the historical evolution by the increase of its dimension, which, by increasing the amount of available behaviours, expresses the technological progress.
These models showed a general social evolution through one only way: in each dimension there were an only ideal behaviour, which tended univocally to predominate. Thus, there were a correspondence between the successive dimensions and the successive predominant behaviours. Perhaps a dimension were overcome before its ideal behaviour arrived to predominate, but it did not alter the linearity of the social evolution.
Only in the last phase there were an effective alternative between the consolidation of a so called Full Repressive Society, FRS (with full repressive capacity) and the transition to a so called Free Scientific Society, FSS (without repressive capacity and with full capacity of scientific communication), which were the ideal behaviours with dimension three and four, respectively, in our model:
We have introduced geographical characteristics in our model [5] in order to distinguish the conditions of inicialization of the individual subsystems according to its location in the population. Also, we weighted the influence of repression and scientific communication according to the distance between the subsystems by means of a factor of Impact. But this did not carry to different evolutive lines in different parts of the population, but only to different velocities of evolution.
Also, the introduction of ecological bounds to the consumption carries, in a last model [6], to a new possibility of finishing the evolution: an Ecological Hecatomb.
In a context of ecological crisis, in which the gain of every behaviour decreases, appears sporadically some anomalous behaviour which is not ideal in any dimension: we speak about Revolt Effect. Nevertheless, this effect is ephemeral, and cannot explain long lines of evolution [7].
These models can provide stimulating explanations for some features of the real evolution of the humanity on the Earth: the historical evolution through the agricultural, industrial and scientific-technological revolutions, the social evolution through different phases of slavery, feudalism and capitalism, the fascist anomalies, the present globalization, and so.
Nevertheless, in the real history of the humanity appears a clear dualism between Orient and Occident. If Godelier [9] already showed that the occidental evolution from slavery to capitalism were singular and not general, the experience of the bureaucratic regimens of Orient shows other singularity which cannot be embedded in the Engels’ scheme [8], but it have not either been a such ephemeral phenomenon to be explained by our Revolt Effect.
Thus, we have to change our model in order to modelize this dual evolution.
Dualizing
We want to obtain not only different ends, but different lines of evolution. In order to distinguish them from the beginning, the differences should to affect to the first dimension of the social behaviour, U0. For it, we can use diverse approaches.
To be gregarious or individualist:
Thus, we could use U0 to modelize the difference Orient/Occident, through the opposition gregariousness/individualism.
We could use the factor of Impact to this purpose.
In the previous model, the Impact decreases linearly with the distance, and it is maximum when the distance d is equal to zero, that is to say, on the self subsystems. This only affects to the repression (between different social behaviours), because the scientific communication refers to interactions between different subsystems.
Now, we will suppose that, if U0 = 0 (gregariousness), the Impact is maximum when d = 0 and decreases with d according to a gaussian curve. But, if U0 = 1 (individualism), its value is multiplied by d, and therefore it values zero when d = 0. That is to say, an individualist social behaviour only represses the other subsystems.
In order to achieve some concordance with the previous model,
we will suppose that the gregarious Impact values 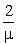 if d = 0
(where µ =
if d = 0
(where µ = 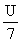 measures the might of the social
behaviour), and effective mean of the individualist Impact
(neglecting the Impact for distances greater than the maximum
distance in the population) is 1. With this conditions, we obtain
i(d) =
measures the might of the social
behaviour), and effective mean of the individualist Impact
(neglecting the Impact for distances greater than the maximum
distance in the population) is 1. With this conditions, we obtain
i(d) = 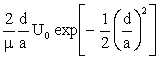 with a =
with a = 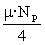 where NP is the amount the population (we suppose
circular distance, and therefore the maximum distance is ½NP).
where NP is the amount the population (we suppose
circular distance, and therefore the maximum distance is ½NP).
Also, we will suppose that U0 only influences the evolution through the factor of Impact.
Regionalizing:
In other approach, we could suppose that each value of U0 has different consequences for subsystems in different locations.
In particular, we will suppose that the first component of the technical possibility of satisfaction, which determines the intrinsic advantage of a social behaviour U, values p0(U,N) = U0(1 – x) + (1 – U0)x ,
with different values of x, between 0 and 1, for different locations N in the population.
Thus, if x=0, p0(U,N) = U0, and therefore the ideal behaviours have to have U0 = 1, that is to say, they are, according the dimension, (1) = 1, (11) = 3, (111) = 7, (1111) =15 = F (in hexadecimal).
On the contrary, if x = 1, p0(U,N) = 1 – U0, and therefore the ideal behaviours have to have U0 = 0, that is to say, they are, according the dimension, (0)=0, (10) = 2, (110) = 6, (1110) = 14 = E .
We have begun to work with this approach because it needs only minor changes in our programs. Thus, we have implemented it in the two last models in which we are working:
- MODAPRHG, a Model of Historical-Geographical evolution [5] with ecological bounds but without recycling. We can find a description of the model in http://www.uv.es/~pla/MODAPRHG.C
- MES, a Model of Social Evolution with recycling. We can find a description of the model in http://www.uv.es/~buso/wacra/wacra_eng.html
x(N) = 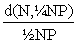 . Therefore, 0 £ x £ 1, with x(¼NP) = 0 and x(¾NP)
= 1 ; as d is a circular distance, x(NP) = x(0) = ½
. Therefore, 0 £ x £ 1, with x(¼NP) = 0 and x(¾NP)
= 1 ; as d is a circular distance, x(NP) = x(0) = ½
Also, we take U = (0) and U = (1) equiprobable in the beginning.
On the contrary, from MES, we make directly x(N)
=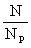 , and therefore x(0) = 0 and x(NP) = 1
, and therefore x(0) = 0 and x(NP) = 1
Also, we take just U = (0) in the beginning.
Results and interpretation
In spite of the serious differences between these two implementations, both carry to similar processes of evolution: 1 ® 3 ® 7 ® F in Occident, 0 ® 2 ® 6 ® E in Orient.
A possible interpretation would be:
- dimension m = 0: primitive societies
- dimension m = 1: agricultural revolution:
- U = 0: oriental empires
- U = 1: occidental slavery
- dimension m = 2: technological changes in
Medieval Age:
- U = 2: oriental feudalism
- U = 3: occidental feudalism
- dimension m = 3: industrial revolution:
- U = 6: socialism of State
- U = 7: capitalism
- dimension m = 4: scientific-technological
revolution:
- U = E, U = F: free scientific societies
The other values of U would represent anomalous social behaviours (fascism, Stalinism, fundamentalism?) which only could appear through the Revolt Effect in extreme situations (war, ecological crisis?).
Note that, if m = 0, there is only one available social behaviour, and therefore there is not evolution: by this reason, ours models begin to run with m = 1.
Also, both U = 7 and U = 6 have full repressive capacity (nuclear weapons?).
Likewise, after m = 3 there are different possibilities of global evolution: definitive predominance of the capitalism, ecological hecatomb or transition to some free scientific society.
Note also that both U = E and U = F have null repressive
capacity; in its own zone, both can have full technical
possibility of satisfaction; and U = 6 has almost full capacity
of scientific communication (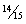 !). For this reason, we name them two kinds of free
scientific society...
!). For this reason, we name them two kinds of free
scientific society...
We have executed ours models with different values of some parameters, in order to search the best approximation to the real evolution of the humanity on the Earth.
We show an interesting result in the table: after a dual evolution with capitalism in Occident and socialism of State in Orient, a globalization of the capitalism arrives. Nevertheless, the ulterior evolution seems to restrict capitalism to its original zone. Unfortunately, the program stopped without showing if this restriction would be overcome or a free scientific society would arrive to predominate...
Note that the number S of active individual subsystems decrease under confrontations (wars?), and the ecology specifically decrease under the confrontation between the full repressive societies U = 6 and U = 7. After the collapse of U = 6 the ecology recovers, but not the number of active individual subsystems in the population.
Conclusions
We have obtained stimulating results, and some ulterior research with our models seems interesting. Nevertheless, the approach of regionalizing in which we have work does not explain why the technical possibilities of satisfaction are different in different locations. Perhaps the first approach about gregariousness/individualism provide us a better explanation, if it permit us to arrive to good results.
Bibliography
D.H.Meadows, D.L.Meadows and J.Randers (1992), "Beyond the Limits", Doubleday Press, New York.
R.Pla-López (1989): "Models of Historical Evolution: alternating ends", Congrès Européen de Systémique, Lausanne.
R.Pla-López (1990), "Models of Multidimensional Historical Evolution", in R.Trappl ed, Cybernetics and Systems'90, World Scientific, Singapore, 575-582.
R.Pla-López (1992), "Model of Adaptive, Historical and Multidimensional Social Learning", in R.Trappls ed, Cybernetics and Systems Research'92, World Scientific, Singapore, 1005-1012.
R.Pla-López (1993), "The Role of Subjective Factor in Social Evolution", in Second European Congress on Systems Science, Prague.
R.Pla-López and V.Castellar-Busó (1994), "Model of Historical-Geographical Evolution", in R.Trappl ed, Cybernetic and Systems'94, World Scientific, Singapore, vol.I, 1049-1056.
V.Castellar-Busó and R.Pla-López (1997), "Un modelo de desarrollo sostenible opuesto a la hecatombe ecológica", in 14th International Conference of WACRA-Europe on Sustainable Development, Madrid.
R. Pla López (1996a), "¿Cuánto puede perdurar una revuelta?", in 1ª Reunión Española de Ciencias de Sistemas, València.
M. Godelier, "Schémas d'evolution des sociétés" (translated to Spanish as "Esquemas de evolución de las sociedades", Miguel Castellote Editor, aprox. in 1970).
- F. Engels (1884), "Der Ursprung aus der Familie, der Privateigentum und der Staat", Zurich (translated to Spanish as "El Origen de la Familia, la Propiedad Privada y el Estado", Fundamentos, Madrid, 1970).
- R. Pla-López (1996b), "Social and Ecological Consequences of Adaptive Pacifism and Unsubmission", in 3rd. European Congress of Systems (CES'3), Roma.