Polígonos convexos

Se dice que una figura es convexa cuando el segmento que determinan dos puntos cualesquiera de la misma está todo él contenido en dicha figura. La luna llena, por ejemplo, es convexa; el cuarto creciente, no:

El círculo es una figura convexa y la media luna no

 En 1942, Fu Traing Wang y Chuan-Chih Hsiung, de la Universidad Nacional de Chekíang, demostraron que en el tangram sólo se pueden construir un máximo de 13 figuras convexas (American Mathematical Monthly, vol. 49) que se proponen al final del texto.

Cualquier figura compuesta por las piezas del tangram puede ser dividida en un total de 16 triángulos isósceles de ángulo recto (triángulos básicos).

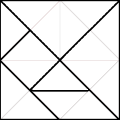
Descomposición en triángulos básicos

Llamaremos lados racionales a los dos lados más cortos y lado irracional al más largo. 

A partir de aquí, Fu Traing Wang y Chuan-Chih Hsiung argumentaron del siguente modo:

Cualquier polígono convexo formado con las piezas del tangram cumple que cada lado racional de cualquier triángulo básico que lo compone se apoya en un lado racional de otro triángulo básico o pertenece al perímetro del polígono (ocurre lo mismo con los lados irracionales).

Todas las piezas del tangram son

• Triángulos cuyos lados racionales (del mismo tipo) forman un ángulo recto y los lados de diferente tipo forman ángulos agudos.

• Un cuadrado cuyos lados son todos racionales (del mismo tipo) y forman ángulos rectos

• Un romboide cuyos ángulos son agudos y obtusos y cuyos lados son racionales e irracionales (de distinto tipo) de forma alterna.

Llamaremos lados racionales del polígono convexo a los que están formados por los lados racionales de los triángulos básicos y lados irracionales a los que están formados por lados irracionales, entonces dos lados consecutivos son del mismo tipo (racionales o irracionales) cuando forman un ángulo recto (90º = 45º + 45º), y diferentes cuando forman un ángulo agudo (45º) u obtuso (135º = 90º + 45º = 45º + 45º + 45º).

Si llamamos  n al número de ángulos y, por lo tanto, también de lados del polígono,  p al número de ángulos agudos, q al número de ángulos rectos, y  r al número de ángulos obtusos tenemos que

 p + q + r = n

Como la suma de todos los ángulos de un polígono convexo de n lados es igual a

(n – 2)·180º

tenemos que

45·p + 90·q + 135·r = (n – 2)·180º

y si eliminamos r nos queda 

2·p + q = 8 – n

Corno p y q tienen que ser iguales o mayores que 0, el polígono podrá tener un máximo de ocho lados y, desde luego, un mínimo de tres lados. Además, los valores de p, q, r y n, se limitan a un número reducido de posibilidades que hemos obtenido con la ayuda de un programa en lenguaje C y que presentamos en la lista siguiente: 

• ocho lados con ocho ángulos obtusos

• siete lados con un ángulo recto y seis obtusos

• seis lados con dos ángulos rectos y cuatro obtusos

• seis lados con un ángulo agudo y cinco obtusos

• cinco lados con tres ángulos rectos y dos obtusos

• cinco lados con un ángulo recto, uno agudo y tres obtusos

• cuatro lados con cuatro ángulos rectos (cuadrado y rectángulo)

• cuatro lados con dos agudos y dos obtusos

• cuatro lados con dos ángulos rectos, uno agudo y uno obtuso y

• tres lados con un ángulo recto y dos agudos (triángulo)

Si en cada caso tenemos en cuenta el número de lados y el número de ángulos que no son rectos, observamos que en ningún polígono convexo tendremos más de cuatro lados irracionales.

Por lo tanto, podemos inscribir cualquiera de estos polígonos convexos dentro de un rectángulo (PQRS), de forma que los lados racionales del polígono ABCDEFGH coincidan con los lados del rectángulo (si todos los lados del polígono son irracionales entonces el polígono y el rectángulo sólo tienen en común los "vértices" del primero).

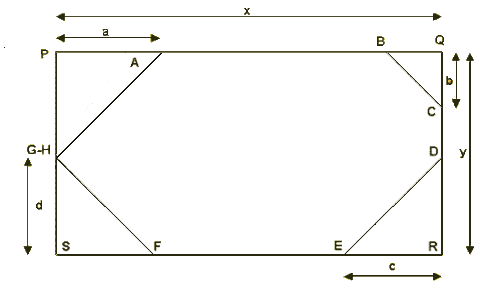
El polígono convexo ABCDEFGH inscrito en el rectángulo PQRS

Si suponemos que la longitud del lado PQ es igual a x veces la longitud del lado racional del triángulo básico, y que para el lado PS es igual a y veces, tendremos que el área del rectángulo PQRS es igual al área del triángulo básico multiplicado por 2xy.

Si los lados irracionales (HA, BC, DE y FG) del polígono convexo tienen una longitud igual a la longitud del lado irracional del triángulo básico multiplicada por a, b, c y d respectivamente (con la posibilidad de que a, b, c o d puden valer cero), tendremos que el área de los triángulos PAH, BQC, DRE y FSG es igual a las área de los triángulos básicos multiplicadas por a², b², c² y d² respectivamente.

Puesto que el polígono está compuesto por 16 triángulos básicos, se deduce que

 a² + b² + c² + d² = 2xy – 16,
cuando a + b  £ x, c + d  £ x, a + d  £ y, b + c  £ y.

Con las soluciones enteras no negativas de esta ecuación resovemos el problema original.

Para acotar el problema podemos suponer quela base del rectángulo PQRS es mayor que su altura, es decir, x ³ y. También podemos suponer que 0 < x  £ 16 porque estos son los casos extremos (que no pueden alcanzarase) correspondientes a que la base del rectángulo PQRS esté formada desde 1 triángulo básico hasta los 16 triángulos básicos.

Hemos obtenido las soluciones enteras y no negativas para la ecuación anterior con la ayuda de un programa en lenguaje C y después de eliminar las soluciones correspondientes a rotaciones y simetrías de polígonos iguales, las presentamos en la tabla:

Volver a la página de inicio

Envía tus comentarios

Vicent Castellar
31 de enero de 2.000
Actualizada el 17 de enero de 2.001

El programa JAVA par jugar al tangram es obra de Jos van Uden y se puede encontrar en