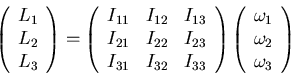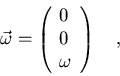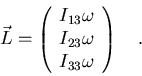

Next: El tensor de inercia
Up: El sólido rígido
Previous: El sólido rígido
Para estudiar el movimiento de un cuerpo, hemos de fijar un sistema de
referencia. Puesto que un cuerpo sólido, a diferencia de una partícula,
tiene dimensiones, vamos a estudiar el movimiento con la ayuda de dos
sistemas de referencia. Un primer sistema de referencia (inercial), en
el
que representemos el movimiento del centro de masas (CM) del sólido, y
un segundo sistema de referencia, cuyo origen sea el centro de masas del
cuerpo, que nos va a informar del movimiento de rotación del sólido. Lo
que estamos haciendo al describir el movimiento con estos dos sistemas
es separar el número de grados de libertad en 3+3 y darnos cuenta de que
hay 3 grados de libertad de traslación y tres grados de libertad de
rotación. Estos tres últimos grados de libertad no están
presentes,
evidentemente, en una partícula puntual. Llamemos 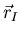 al
radiovector de un cierto punto del sólido, visto desde el sistema
inercial,
al
radiovector de un cierto punto del sólido, visto desde el sistema
inercial,
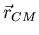 a la posición del CM del sólido y
a la posición del CM del sólido y 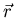 al
mismo punto visto desde el sistema de referencia situado en el CM:
al
mismo punto visto desde el sistema de referencia situado en el CM:
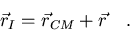 |
(7.2) |
Derivando respecto al tiempo,
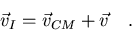 |
(7.3) |
Si el sólido tiene un movimiento exclusivamente de traslación (los
ángulos entre los ejes de ambos sistemas no cambian), entonces
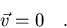 |
(7.4) |
Si el sólido gira,
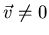 ,
pero ya que se trata de un movimiento
de rotación, es más conveniente escribir
,
pero ya que se trata de un movimiento
de rotación, es más conveniente escribir
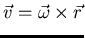 ,
donde
,
donde
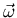 es un vector cuya magnitud indica la velocidad de
giro y cuya dirección es la del eje respecto al cual se produce el
giro.
La energía cinética del sólido será
es un vector cuya magnitud indica la velocidad de
giro y cuya dirección es la del eje respecto al cual se produce el
giro.
La energía cinética del sólido será
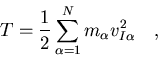 |
(7.5) |
donde N es el número de partículas que lo componen. Pero
es más conveniente tratar el sólido como un medio continuo. En
lugar de
sumar sobre las partículas, hemos de integrar sobre elementos de
masa
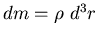 ,
siendo
,
siendo 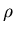 la densidad del medio. Así,
la densidad del medio. Así,
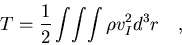 |
(7.6) |
donde 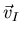 es la velocidad que tiene, en un instante dado, el
elemento de volumen d3r con masa
es la velocidad que tiene, en un instante dado, el
elemento de volumen d3r con masa
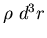 .
Escribiendo
.
Escribiendo 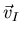 en términos de
en términos de
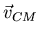 y
y 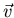 ,
,
![\begin{displaymath}\begin{array}{lll}
T&=&\displaystyle\frac{1}{2}\int\!\int\!\...
... r\ )
+(\vec\omega\times\vec r\ )^2]d^3r\quad .
\end{array}
\end{displaymath}](img33.gif) |
(7.7) |
Calculemos cada una de las contribuciones por separado. La primera,
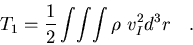 |
(7.8) |
Pero
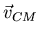 no depende de
no depende de 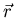 ,
y la integral
,
y la integral
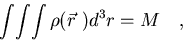 |
(7.9) |
la masa del sólido, luego
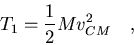 |
(7.10) |
es la energía cinética correspondiente al CM del sólido, la única
contribución si se tratara de una partícula libre.
El segundo término,
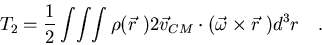 |
(7.11) |
Intercambiando el producto mixto,
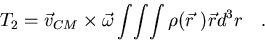 |
(7.12) |
Para ver mejor su valor, escribamos la integral en forma de suma:
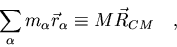 |
(7.13) |
siendo
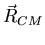 la coordenada del centro de masas. Pero esta
integral la estamos haciendo justamente en el sistema de referencia del
centro de masas, es decir,
la coordenada del centro de masas. Pero esta
integral la estamos haciendo justamente en el sistema de referencia del
centro de masas, es decir,
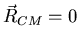 ,
luego
,
luego
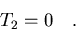 |
(7.14) |
Desarrollando el producto vectorial, podemos reescribir
el último término como:
![\begin{displaymath}\begin{array}{lll}
(\vec\omega\times\vec r\ )^2&=&\omega^2r^...
...\omega_i\omega_j[\delta_{ij}r^2-x_ix_j]
\quad ,
\end{array}
\end{displaymath}](img43.gif) |
(7.15) |
donde xi son las componentes cartesianas de  .
Por tanto,
.
Por tanto,
![\begin{displaymath}T_3=\frac{1}{2}\sum_{i,j}\omega_i\omega_j
\int\!\int\!\int\rho(\vec r\ )
[\delta_{ij}r^2-x_ix_j]d^3r
\end{displaymath}](img44.gif) |
(7.16) |
Es conveniente introducir la delta de Kronecker para extraer de forma
unívoca
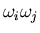 .
Introduciendo la cantidad Iij
denominada
tensor de inercia,
.
Introduciendo la cantidad Iij
denominada
tensor de inercia,
![\begin{displaymath}I_{ij}=\int\!\int\!\int\rho(\vec r\ )
[\delta_{ij}r^2-x_ix_j]d^3r\quad ,
\end{displaymath}](img46.gif) |
(7.17) |
la expresión de T3 adquiere la forma sencilla
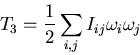 |
(7.18) |
La energía cinética finalmente es:
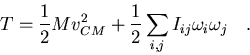 |
(7.19) |
El primer término recibe el nombre de energía cinética de traslación y
el segundo energía cinética de rotación. El tensor de inercia puede
escribirse en forma matricial:
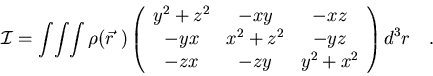 |
(7.20) |
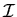 es un tensor simétrico por definición, es decir, tiene como máximo 6
componentes distintas.
Antes de estudiar con detalle el tensor de inercia y entender un poco
más su significado, vamos a hallar el momento angular, cantidad con
la que
es un tensor simétrico por definición, es decir, tiene como máximo 6
componentes distintas.
Antes de estudiar con detalle el tensor de inercia y entender un poco
más su significado, vamos a hallar el momento angular, cantidad con
la que  está íntimamente relacionado.
Nuevamente nos referimos a los dos sistemas de referencia anteriores.
Tendremos por tanto:
está íntimamente relacionado.
Nuevamente nos referimos a los dos sistemas de referencia anteriores.
Tendremos por tanto:
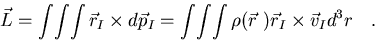 |
(7.21) |
Pero
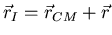 y
y
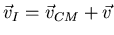 .
Sustituyendo en la ecuación anterior, salen ahora cuatro términos del
producto vectorial:
.
Sustituyendo en la ecuación anterior, salen ahora cuatro términos del
producto vectorial:
![\begin{displaymath}\begin{array}{lll}
\vec L&=&
\displaystyle\int\!\int\!\int\...
...es\vec r+\vec r\times(\omega\times\vec r\ )]d^3r
\end{array}
\end{displaymath}](img54.gif) |
(7.22) |
Los dos términos intermedios se anulan porque contienen 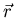 solamente si el segundo sistema toma como origen el centro de masas del
cuerpo. El primer término da lugar al momento angular del centro
de masas,
solamente si el segundo sistema toma como origen el centro de masas del
cuerpo. El primer término da lugar al momento angular del centro
de masas,
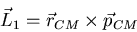 |
(7.23) |
y el cuarto término tiene que dar lugar a la contribución de la rotación
del sólido al momento angular total, lo que llamaremos momento angular
interno. Veamos cómo.
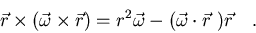 |
(7.24) |
La componente i valdrá
![\begin{displaymath}[\vec r\times(\vec\omega\times\vec r\ )]_i=
r^2\omega_i-\sum_j\omega_j x_jx_i\quad .
\end{displaymath}](img57.gif) |
(7.25) |
Si multiplicamos el primer término por
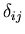 ,
podemos
sumar en
i y en j, con lo que la ecuación anterior adquiere la forma
,
podemos
sumar en
i y en j, con lo que la ecuación anterior adquiere la forma
de donde se obtiene
![\begin{displaymath}L_i=\sum_j\omega_j\int\!\int\!\int\rho(\vec r\ )[r^2\delta_{ij}-x_ix_j]
d^3r=\sum_jI_{ij}\omega_j\quad .
\end{displaymath}](img60.gif) |
(7.26) |
En forma matricial,
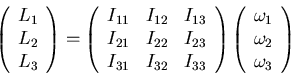 |
(7.27) |
o, en forma abreviada,
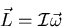 |
(7.28) |
donde 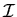 es un tensor de rango dos.
es un tensor de rango dos. 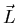 y
y
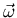 no
están unidos por una relación escalar, lo que significa que
no
están unidos por una relación escalar, lo que significa que
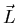 no va a ser paralelo a
no va a ser paralelo a
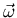 en general. Si, por ejemplo,
en general. Si, por ejemplo,
tendremos que
Como consecuencia de esto, si 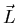 se conserva en un sistema
aislado, y nos imaginamos que un sólido está describiendo un
movimiento
de rotación, el eje de giro no tiene porqué permanecer constante, ya que
no coincide con el eje de
se conserva en un sistema
aislado, y nos imaginamos que un sólido está describiendo un
movimiento
de rotación, el eje de giro no tiene porqué permanecer constante, ya que
no coincide con el eje de 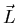 .
Para finalizar, el momento angular
total del sólido será
.
Para finalizar, el momento angular
total del sólido será
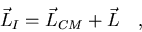 |
(7.29) |
el momento angular del centro de masas más el momento angular
interno.


Next: El tensor de inercia
Up: El sólido rígido
Previous: El sólido rígido
Andres Cantarero
1998-12-06
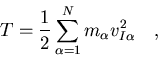
![\begin{displaymath}\begin{array}{lll}
T&=&\displaystyle\frac{1}{2}\int\!\int\!\...
... r\ )
+(\vec\omega\times\vec r\ )^2]d^3r\quad .
\end{array}
\end{displaymath}](img33.gif)
![\begin{displaymath}\begin{array}{lll}
(\vec\omega\times\vec r\ )^2&=&\omega^2r^...
...\omega_i\omega_j[\delta_{ij}r^2-x_ix_j]
\quad ,
\end{array}
\end{displaymath}](img43.gif)
![\begin{displaymath}T_3=\frac{1}{2}\sum_{i,j}\omega_i\omega_j
\int\!\int\!\int\rho(\vec r\ )
[\delta_{ij}r^2-x_ix_j]d^3r
\end{displaymath}](img44.gif)
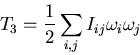
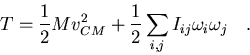
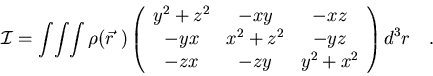
![\begin{displaymath}\begin{array}{lll}
\vec L&=&
\displaystyle\int\!\int\!\int\...
...es\vec r+\vec r\times(\omega\times\vec r\ )]d^3r
\end{array}
\end{displaymath}](img54.gif)
![\begin{displaymath}[\vec r\times(\vec\omega\times\vec r\ )]_i=
r^2\omega_i-\sum_j\omega_j x_jx_i\quad .
\end{displaymath}](img57.gif)
![\begin{displaymath}\sum_{i,j}\omega_j[r^2\delta_{ij}-x_ix_j]\quad ,\end{displaymath}](img59.gif)
![\begin{displaymath}L_i=\sum_j\omega_j\int\!\int\!\int\rho(\vec r\ )[r^2\delta_{ij}-x_ix_j]
d^3r=\sum_jI_{ij}\omega_j\quad .
\end{displaymath}](img60.gif)