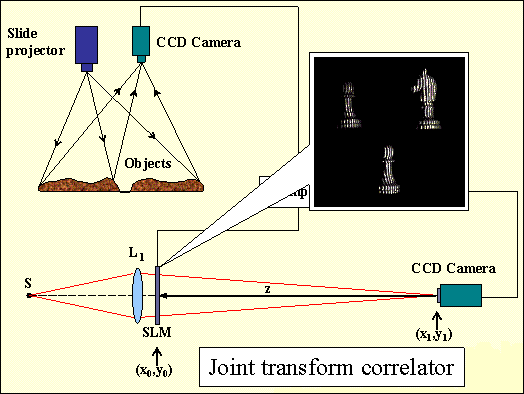
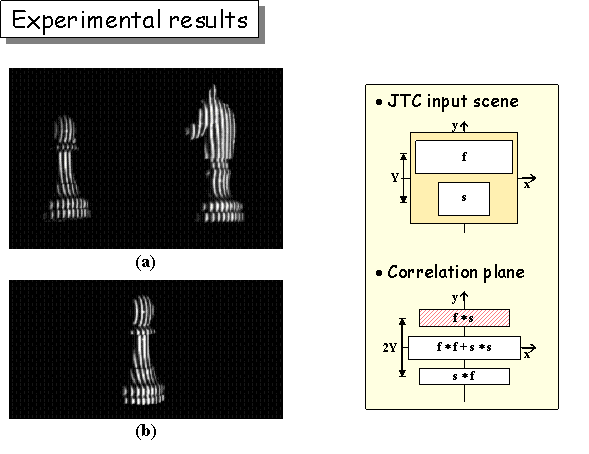
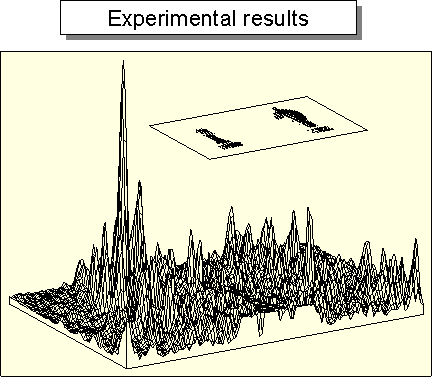
Tridimensional optical image recognition

Recognition of three-dimensional (3-D) objects is an increasing important issue in the field of optical pattern recognition. For instance, there are applications in which the important object information is not contained in just one 2-D projection, but in all its 3-D shape.

One of our research areas is the 3-D object recognition based on Fourier transform profilometry (FTP). This technique is based on projecting a regular fringe pattern onto the surface of a 3-D object and capturing with a CCD camera a 2-D image of the resultant scene. The obtained image is a deformed grating pattern which carries all the 3-D information of the object. The sketch of the experimental optical setup for Fourier transform profilometry technique is shown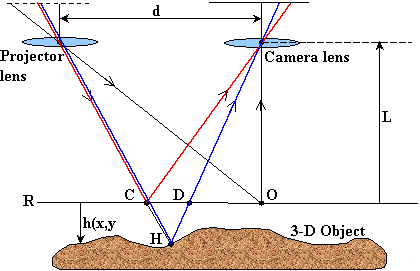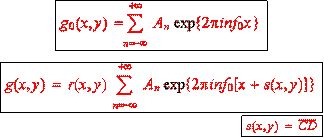

EXTENSION TO 3-D ROTATIONS TRIDIMENSIONAL DETECTION INVARIANT

We will use range images. A range image, z=f(x,y), contains the depth information of an object from a given view line, that defines the z axis.

The rotation of the 3-D object changes the 3-D range image. Note that the range image is a single valued function, therefore only the part of the surface closer to the positive z axis is contained on it. The encoding of the depth information has been used in the literature to extend the possibilities of range images. Following this approach, we encode the range image as phase as follows

P(x,y)=exp[iwz(x,y)]

where w is a constant that permits the adjustment of the phase slope of the object. A way to deal with range images keeping translation invariance is to use their Fourier transform. The Fourier transform of the phase encoded range image (PhFT) is then

PhFT(u,v)=F_2D{exp[iwz(x,y)]}

where stands for two dimensional Fourier transform. Note that w determines the scaling of the Fourier transform frequencies. From now, we will assume w=1, that correspond to the PhFT mapping detailed in the following. A planar surface of the object, after phase encoding, will become a linear phase factor. Thus its Fourier transform will be peaked around a well defined location.

The main effect of 3D small rotations in z axis is a shift in the FT! Matching can be made on the PhFT instead of in the range image. Because of that we use common linear correlation in order to obtain z-axis rotation invariant 3-D object recognition.

We will compose a global 3-D Object Orientation Map (3DOOM).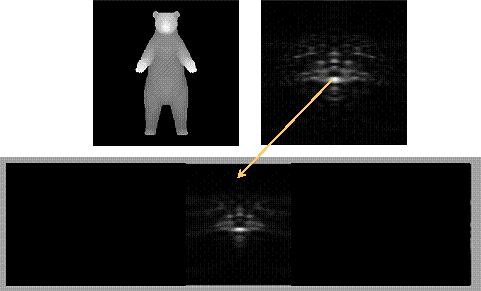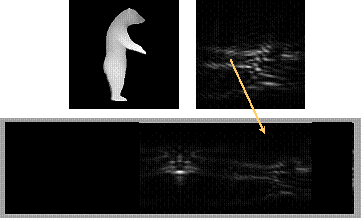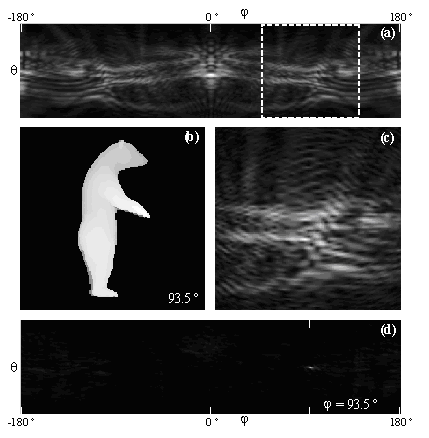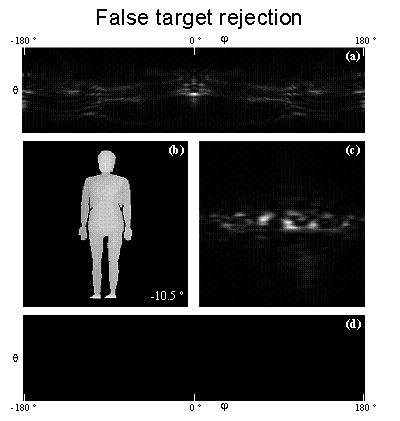

Axes choice changes the 3DOOM

The PhFT of each view correspond to a portion of the 3DOOM, although distorted and shifted

Object rotation gives a general rotation of the 3DOOM in spherical coordinates.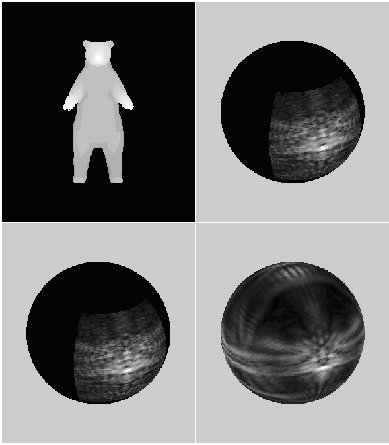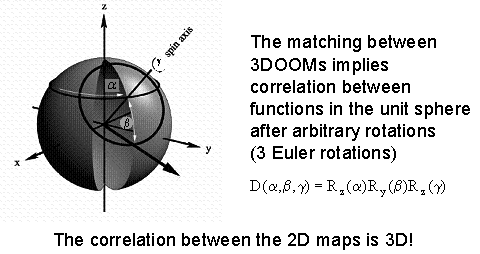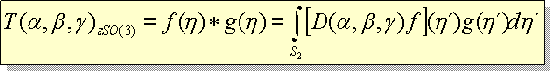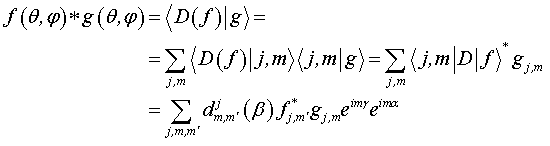

Example with only two rotations (a and b) and translations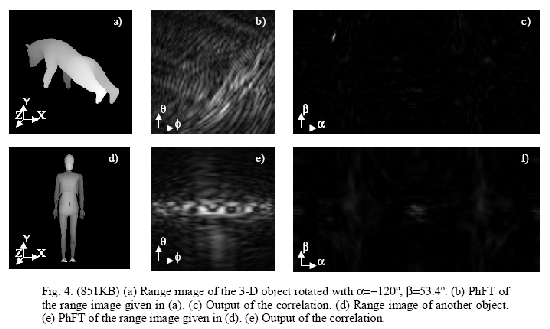

PAPERS ON THE SUBJECT:

• J. J. Esteve-Taboada, J. García and C. Ferreira, "Optical recognition of three dimensional objects with scale invariance using classical convergent correlator," Opt. Eng. 41, 1324-1330 (2002).
• J. J. Esteve-Taboada, Ph. Refregier, J. Garcia and C. Ferreira, "Target localization in the three-dimensional space by wavelength multiplexing," Opt. Commun. 292, 69-79 (2002).
• J. J. Esteve-Taboada and J. García, "Detection and orientation evaluation for three-dimensional objects," Opt. Commun. 217, 123-131 (2003).
• J. García, J. J. Vallés and C. Ferreira, "Detection of three-dimensional objects under arbitrary rotations based on range images," Opt. Express 11, 3352-3358 (2003).
• J. J. Esteve-Taboada, N. Palmer, J.-C. Giannessini, J. García and C. Ferreira, "Recognition of polychromatic three-dimensional objects," Appl. Opt. 43, 433-441 (2004).
• C. Ferreira, J. García, P. García-Martínez, H. H. Arsenault, J. J. Esteve-Taboada and J. J. Vallés, "Correlaciones para el reconocimiento de imágenes de intensidad (2D) y de rango (3D)," Opt. Pura y Aplicada 38, 21-33 (2005).