1. Elegimos aleatoriamente
varias calles de un pueblo. Una vez elegidas las calles, se entrevista a todos
los vecinos de esas calles. Estamos ante un muestreo:
A) Estratificado
B) Por conglomerados
C) Poli-etápico
2. Se quiere examinar si, en
los matrimonios, la esposa es más maquiavélica que su marido. Se seleccionan 20
parejas, y se obtiene la puntuación en maquiavelismo de cada una de ellos. Si
decidimos efectuar una prueba no paramétrica, elegiremos la prueba de:
A) Wilcoxon
B) Mann-Whitney
C) Kruskal-Wallis
3. Se quiere examinar si
la variabilidad (dentro de la población) en la variable “sociabilidad”
varía entre vecinos de zonas rurales (con una muestra aleatoria de 10 personas)
y de zonas urbanas (con una muestra aleatoria de 10 personas). ¿Qué prueba
podremos efectuar para evaluar esta pregunta?:
A) Levene
B) Mauchly
C) Friedman
4. Seis personas pasan por
los 3 niveles de la variable independiente “Color del aula”, y la
var.dependiente es el TR. Antes del ANOVA efectuaremos la prueba de:
A) Levene
B) Mauchly o La correción
epsilon
C) Ninguna, dado que con 3
niveles el supuesto de homogeneidad de varianzas siempre se cumple
5. Hemos hecho un
experimento en el que no hemos encontrado un efecto significativo del factor.
Sabemos que muchos otros investigadores sí lo han obtenido. Quizás hemos podido
cometer un error de tipo:
A) I
B) III
C) II
6. ¿Cuál de los supuestos
en un ANOVA unifactorial entresujetos, con n igual para cada nivel, tiene
consecuencias más graves en caso de incumplirse?
A) Normalidad
B) Homogeneidad de
varianzas
C) Independencia de
puntuaciones
7. Si nos dicen que, en un
contraste de medias, b=.96, ello quiere decir que:
A) La probabilidad de
error tipo II es muy alta.
B) La probabilidad de
error tipo II es muy baja.
C) La probabilidad de
error tipo I es muy alta.
8. Hemos obtenido un valor
de “sig=1.000” en un ANOVA intra-sujetos con 3 niveles. Ello implica que:
A) La hipótesis nula es
necesariamente falsa.
B) La hipótesis nula es
necesariamente cierta.
C) Las 3 medias son
iguales.
9. Antes de efectuar una
prueba t hemos realizado la prueba de Levene, y ésta ha mostrado un valor de
“sig=.012”. Habremos de asumir:
A) Varianzas diferentes
B) Varianzas iguales
C) Medias iguales
10. Hemos calculado la
prueba V de Cramer, para evaluar la relación entre género (hombre, mujer) y
consumo de drogas (nunca, a veces, habitualmente) y tenemos un valor de
“sig=.02”. Ello indica:
A) Una relación
significativa entre género y consumo
B) Una relación no
significativa entre género y consumo
C) Una relación lineal
entre ambas variables
11. ¿Qué estadísticos de
la lista son CONSISTENTES?:
A) La media, varianza y
cuasivarianza muestrales
B) La media y
cuasivarianza muestrales, no la varianza
C) La varianza y
cuasivarianza muestrales, no la media
12. El error típico de la
media es:
A) la desviación típica de
la distribución muestral de la media
B) la probabilidad de
cometer error de tipo I al tomar la media muestral como indicador del parámetro
C) el error más frecuente
que se comete al calcular la media muestral
13. Un psicólogo afirma
que el 70% de la población lee la revista “Y”. Para evaluar dicha afirmación
preguntamos a 100 personas, de las que 62 afirman leerla. Podemos concluir que:
A) Hemos encontrado diferencias
en las proporciones
B) No hay diferencias
significativas en las proporciones
C) La pregunta no ha
lugar, dado que no hay pruebas inferenciales sobre proporciones
A) Aumentan
B) Disminuyen
C) Se mantienen constante
15. Hemos efectuado la
corrección de Bonferroni. Los contrastes habrán sido:
A) A priori
B) A posteriori
C) Necesariamente no
paramétricos
16. (TABLA 1) ¿Cuántos
sujetos participaron en el experimento?:
A) 14
B) 15
C) 16
17. (TABLA 1) ¿Cuál es el
valor de
A) 1.833
B) 1.655
C) 1.233
18. (TABLA 1) ¿Podemos
concluir que el efecto de contexto varía significativamente con la edad?:
A) Sí
B) No
C) Un ANOVA no permite
efectuar tal inferencia
19. Tenemos 2 grupos
control y 1 grupo experimental, y queremos evaluar si hay diferencias (respecto
a las medias) entre los grupos control (tomados conjuntamente) y el grupo
experimental. Efectuaremos pues un contraste:
A) Complejo
B) Sencillo
C) Aleatorio
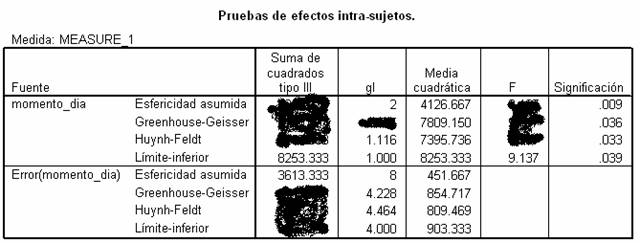
20. (TABLA 2) ¿Cuál es el
valor de la corrección epsilon-GG:
A) 0’548
B) 0’558
C) 0’528
21. (TABLA 2) Si el ANOVA
hubiese sido entre-sujetos, ¿cuál hubiera sido la Suma de Cuadrados del
numerador?:
A) 8253’3
B) 8253’3 dividido por 2
C) Habría que calcularla
con los datos originales
22. (TABLA 2) ¿Cuántos
sujetos participaron en el experimento?:
A) 5
B) 6
C) 7
23. Hemos analizado la
relación entre Estado Civil (soltero, casado, viudo/divorciado) y Tipo de
películas favorita (drama, comedia, acción). Si la chi-cuadrado empírica a
partir de la tabla de contingencia es ligeramente menor que el percentil 95 de
la tabla de chi-cuadrado apropriada, concluiremos:
A) Que no hay relación
significativa entre las variables.
B) Que hay relación
significativa entre las variables.
C) El estadístico
chi-cuadrado no se emplea en tal caso.
24. (TABLA 3) Indica la
frase adecuada respecto al experimento descrito
A) Frase A
B) Frase B
C) Frase C
Tabla 1.
Tenemos un diseño
factorial entre-sujetos (con el mismo “número de sujetos” para cada condición
experimental) donde manipulamos el Contexto (mismo vs. diferente) y
(Utilizad TODOS
los decimales para hacer las pruebas.)
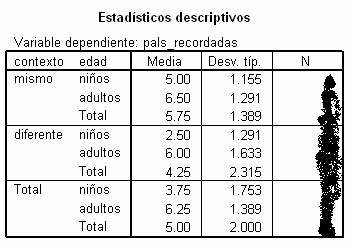
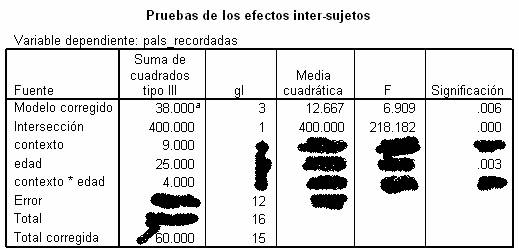
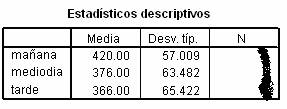
TABLA 2. Tenemos
un diseño unifactorial intra-sujeto. Se efectúa (en 3 sesiones) una tarea
simple de tiempo de reacción con sujetos extravertidos. Las sesiones tienen
lugar por la mañana, mediodía y tarde. Cada sujeto pasa por las tres
condiciones experimentales.
-------------------------------------------------------------------------------
TABLA 3. Se ha efectuado un tratamiento a un grupo de seis fumadores. Tenemos el número de cigarrillos promedio (durante una semana) ANTES del tratamiento y DESPUÉS del tratamiento. El output de la prueba estadística apropiada es el siguiente:
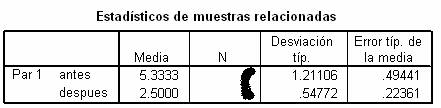

Concluiremos que…(INDICA
A) El tratamiento ha producido un descenso significativo
en el número de cigarrillos fumados, t(6)=7’06, p<0’05.
B) El tratamiento ha producido un descenso significativo
en el número de cigarrillos fumados, t(5)=7’06, p<0’05.
C) No tenemos evidencia suficiente para afirmar que el
tratamiento haya influido en el número de cigarrillos fumados, t(6)=7’06,
p>0’05.