1. Un filólogo está haciendo un estudio en el que pregunta a una muestra de estudiantes universitarios "¿cuántos libros de Milan Kundera has leído?". ¿Qué escala de medida tendremos?

A) Escala de razón

B) Escala ordinal

C) Escala de intervalo

2. Un informático pregunta a una serie de estudiantes cuál es el sistema operativo con el que trabajan habitualmente en sus respectivos ordenadores (1-Window$, 2-MacOS, 3-Linux/UNIX, 4-BeOS, 5-Otros). ¿Qué estadísticos emplearás para medir la "tendencia central"?

A) Moda

B) Moda o Mediana

C) Moda, Mediana o Media

3. Una muestra de críticos de cine evalúa la película Eraserhead (Cabeza_Borradora) de David Lynch bien como "1-muy mala", "2-mala", "3-normal", "4-buena" o "5-excelente". ¿Qué tipo de escala tendremos?

A) Intervalo

B) Ordinal

C) Nominal

4. Cien trabajadores de la T.I.A. viven a lo largo de la calle "Rue del Percebe". 10 trabajadores viven en el número 112, 30 trabajadores en el número 150, 5 trabajadores en el número 152, 5 trabajadores en el número 156, 20 trabajadores en el número 200, y el resto vive en el número 250. Los trabajadores van andando al trabajo y son todos (aproximadamente) igual de veloces al andar. ¿En qué número de la calle pondrías la oficina en la que trabajan para minimizar la distancia recorrida los trabajadores?

A) En el número 158

B) Las otras respuestas son correctas

C) En el número 156

5. En cierta asignatura, sabemos que el examen de marzo pesa la cuarta parte que el examen de junio. Si un estudiante ha obtenido un 6 en el examen de marzo, y un 4'2 en el examen de junio, ¿qué nota final obtendrá?

A) 4'80

B) 4'56

C) 4'68

6. Queremos calcular la media recortada al 5% para las puntuaciones de cierta prueba con 10 estudiantes (4, 5, 5, 3, 6, 7, 9, 7, 6, 10). Indica el valor de la misma:

A) 6’00

B) 6’17

C) 5’88

7. Con las 10 puntuaciones del ejercicio anterior (4, 5, 5, 3, 6, 7, 9, 7, 6, 10), calcula la media winsorizada a nivel 1:

A) 6’3

B) 6’2

C) 6’4

8. Un estudiante se ha inventado el siguiente estadístico: (DM+Q)/2 ¿Qué es lo que mide dicho estadístico?

A) Variabilidad

B) Asimetría

C) Tendencia central

9. Un matemático ha inventado el siguiente estadístico de asimetría: (Md-Mo)/s_x Cuando el valor de dicho estadístico sea mayor que 0: (NOTA: Recordad las relación entre los estadísticos de tendencia central en distribuciones asimétricas)

A) Sirve para indicar cierta asimetría negativa

B) Sirve para indicar simetría total

C) Sirve para indicar cierta asimetría positiva

10. Si empleamos una transformación de la "escalera de Tukey" (v.g., la raíz cuadrada o el logaritmo), estaremos alterando las medidas de:

A) Tendencia central, variabilidad y forma (simetría/asimetría)

B) Tendencia central y variabilidad, únicamente

C) Tendencia central, únicamente.

11. Cuando pasamos una serie de datos desde puntuaciones directas a puntuaciones típicas, la distribución resultante tendrá (necesariamente):

A) media 0, desviación típica 1, y será simétrica

B) media 0 y desviación típica 1

C) media 0, desviación típica 1, será simétrica y seguirá la distribución normal.

12. Sabemos que los predictores Z y W predicen (conjuntamente en el plano de regresión) el 49% de la varianza de la variable predicha Y. ¿Cuál será el valor del índice de correlación múltiple?

A) 0'70

B) 0'70 ó -0'70

C) 0'49 ó -0'49

13. Sabemos que el predictor T predice el 64% de la varianza de la variable predicha Y. ¿Cuál será la pendiente de la recta de regresión de Y a partir de T en puntuaciones típicas?

A) 0'80 ó -0'80

B) 0'80

C) 0'64 ó -0'64

14. En una variable aleatoria continua tenemos que en su función de densidad, f(3)=2'3. ¿ Es eso posible?

A) No, ha debido haber algún error en los cálculos

B) La función de densidad sólo se aplica a variables aleatorias discretas

C) Sí, es posible

15. Sabemos que la varianza de Y explicada por X es de 10, y que la varianza total de Y es de 20. ¿Qué porcentaje de varianza comparten ambas variables?

A) 25%

B) 50%

C) 30%

16. ¿Cuándo podemos tener problemas de colinealidad (multicolinealidad) en regresión lineal múltiple?

A) Cuando los predictores tienen bajas correlaciones entre sí

B) Cuando los predictores correlacionan altamente entre sí

C) Cuando los predictores muestran asimetría negativa en sus distribuciones univariadas.

17. Si tenemos una distribución t de Student con 900 grados de libertad, se puede decir que:

A) Tenemos esencialmente una distribución normal, con media 0 y desviación típica desconocida

B) Tenemos esencialmente una distribución normal, con media y desviación típica desconocidas.

C) Tenemos esencialmente una distribución normal con media 0 y desviación típica 1

18. Pensemos que "número de escritores" (X) que los estudiantes conocen correlaciona positivamente con la nota de un examen de filología (Y). Asumamos que la ecuación de regresión fuera de Y´=0'4+0'20X. ¿Cuántos escritores habrás de conocer para que la recta de regresión prediga que has sacado un 5 en el examen?

A) 23

B) 24

C) 25

19. Un pirata de la red telefónica ha observado que el número de llamadas entre el portavoz del gobierno conservador y el jefe de informativos de la televisión estatal correlaciona positivamente con el número de informaciones de corte "tendencioso/parcial" en los telediarios del estado. Con la información anterior, se puede concluir:

A) Que las llamadas del gobierno causan la "tendenciosidad" de la información

B) Que hay una covariación entre ambas medidas, pero se precisan más datos para evaluar la causalidad

C) Que las llamadas del director de informativos provocan mayor conservadurismo en el gobierno.

20. Un individuo ocupa el percentil 33 en una prueba psicológica, de la que sabemos que la media es 10, que la varianza es 2'25, y que las medidas en la prueba siguen una distribución normal. ¿Qué puntuación directa (aproximadamente) habrá obtenido nuestro individuo?

A) 9'01

B) 8'79

C) 9'34

21. Queremos predecir la variable RENDIMIENTO a partir de la variable DISTANCIA_A_LA_UNIVERSIDAD. Después de introducir los datos en el SPSS, vamos al menú "Analizar" y de ahí a "Regresión". El "output" del ordenador viene dado en la Tabla 1. Dado dicho output, ¿cuál es el porcentaje de varianza común entre ambas variables?

A) 20’9%

B) 10’5%

C) 4’3%

22. Tenemos un conjunto de datos de la variable calificación de cierto examen. Se ofrecen algunos datos del "output" de SPSS en la Tabla 2. ¿Cuál de los tres diagramas de caja y bigotes será el que corresponda a los datos?

A) Gráfico A

B) Grafico B

C) Gráfico C

23. Queremos predecir la variable TIEMPO_REACCIÓN a partir de los predictores EDAD y MOTIVACIÓN. Hemos ido a SPSS y el "output" del ordenador viene en la Tabla 3. Se pide que indiques la ecuación del plano de regresión en puntuaciones DIFERENCIALES.

A) tr’=-1’74·edad-2’31·motiv

B) tr’=-0’08·edad-1’11·motiv

C) tr’=541’4-1’74·edad-2’31·motiv

24. ¿Qué tipo de asimetría tenemos en la variable MOTIVACIÓN, de la cual tenemos su diagrama de tallo-y-hojas en el SPSS (Tabla 4)?

A) Asimetría negativa

B) Asimetría positiva

C) Totalmente simétrica

Tabla 1.

Coeficientes(a)

Modelo		Coeficientes no estandarizados		Coeficientes estandarizados	t	Sig.
		B	Error típ.	Beta
1	(Constante)	3.658	.841		4.349	.001
	DISTANCI	.105	.156	.209	.676	.514

a Variable dependiente: RENDIM

Tabla 2.

Percentiles

		Percentiles
		5	10	25	50	75	90	95
Promedio ponderado(definición 1)	Calific	.0000	2.4000	5.0000	7.0000	12.0000	16.2000	.
Bisagras de Tukey	Calific			5.0000	7.0000	10.5000

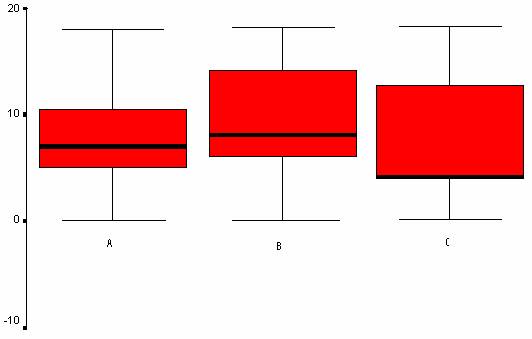
Tabla 3

Coeficientes(a)

Modelo		Coeficientes no estandarizados		Coeficientes estandarizados	t	Sig.
		B	Error típ.	Beta
1	(Constante)	541.378	72.558		7.461	.000
	EDAD	-1.743	9.412	-.080	-.185	.856
	MOTIVAC	-2.307	8.805	-.113	-.262	.798

a Variable dependiente: TR

Tabla 4.

MOTIVAC Stem-and-Leaf Plot

Frequency Stem & Leaf

1.00 0 . 1

2.00 0 . 22

10.00 0 . 4444445555

7.00 0 . 6666667

1.00 0 . 9

2.00 1 . 01

2.00 1 . 23

2.00 1 . 55

1.00 1 . 7

1.00 1 . 8

1.00 Extremes (>=27)

Stem width: 10.00

Each leaf: 1 case(s)