1. Tenemos un ANOVA intra-sujetos cuya F empírica es F(2,14)=4’54 (sin corrección de epsilon). ¿Cuántos sujetos participaron en el experimento?:

A) 8

B) 7

C) 6

2. Si se disminuye el tamaño de la muestra, la potencia de un contraste:

A) Disminuye.

B) Aumenta.

C) Se mantiene constante.

3. ¿Cuál es la prueba no paramétrica paralela a la t de Student de grupos no relacionados?:

A) Mann-Whitney

B) Kruskal-Wallis

C) Wilcoxon

4. Supongamos que, en Valencia, 90% de los estudiantes universitarios van a centros públicos y el 10% a privados. Si queremos 100 estudiantes, y lo que hacemos es dividir los alumnos en 2 grupos (pública y privado), para elegir aleatoriamente 90 estudiantes de la pública y aleatoriamente 10 de la privada tendremos:

A) Un muestreo estratificado

B) Un muestreo por conglomerados

C) Un muestreo polietápico

5. En términos de eficiencia:

A) La varianza muestral es más eficiente que la cuasivarianza muestral.

B) La cuasivarianza muestral es más eficiente que la varianza muestral.

C) La cuasivarianza muestral es igual de eficiente que la varianza muestral.

6. Cuando reducimos la probabilidad de error de tipo I, la potencia de una prueba estadística:

A) Disminuye.

B) Aumenta.

C) Se mantiene constante.

7. El índice phi se interpreta de manera análoga al coeficiente de:

A) Pearson (excepto que phi varía de 0 a 1)

B) Wilcoxon

C) Friedman

8. En regresión lineal simple, si el coeficiente de Pearson es significativo:

A) El coeficiente de la pendiente también lo será.

B) El coeficiente de Pearson valdrá más de 0’25.

C) El coeficiente de la ordenada en el origen también lo será.

9. (TABLA 1) Indica el valor de epsilon de GG:

A) 0’652

B) 0’787

C) 0’791

10. (TABLA 1) Indica cuántos sujetos participaron en el experimento:

A) 6

B) 7

C) 13

11. (TABLA 2) ¿Cuál es el valor de “p” apropiado para el contraste de medias?

A) 0’468

B) 0’480

C) 0’006

12. (TABLA 2) ¿Cuál es el valor de “x” en los intervalos de confianza para la diferencia de medias?

A) -9’48

B) 0’56

C) Con los datos que tenemos, podría ser cualquiera de las otras respuestas

13. Tenemos una distribución asimétrica y queremos hacer una transformación que la haga algo más simétrica. La transformación que haremos será:

A) Raíz Cuadrada

B) Pasar los datos a puntuaciones diferenciales

C) Pasar los datos a puntuaciones típicas

14. Calcula la media recortada al 5% de los siguientes datos: 6, 4, 7, 3, 9, 1, 10.

A) 5.74

B) 5.71

C) 5.66

15. Tenemos una escala de intervalo, por lo que podremos computar para la tendencia central:

A) Tanto la moda, la mediana como la media

B) La moda y la mediana, pero no la media

C) La mediana, pero no la media ni la moda

16. La variable “número de veces que he subido en avión” es:

A) cuantitativa discreta

B) cuantitativa continua

C) cuasicuantitativa

17. Tenemos un valor extraído (0’0) de una distribución F de Fisher con 2 grados de libertad en el numerador, y 10 en el denominador. ¿Qué área de la distribución dejará por encima?:

A) 0’5

B) 1’0

C) 0’0

18. Tenemos una variable aleatoria discreta, en la que nos dicen que, en la función de probabilidad, que f(0)=1’5. ¿Es eso posible?:

A) Sí, es posible.

B) La función de probabilidad sólo se aplica a variables aleatorias continuas.

C) No, no es posible.

19. Tenemos una distribución es asimétrica negativa, y que la mediana es 6; la moda será presumiblemente:

A) mayor de 6.

B) menor de 6.

C) exactamente 6.

20. ¿Cuándo podemos tener problemas de multicolinealidad?:

A) Cuando los predictores correlacionan altamente entre sí.

B) Cuando tanto los predictores como las predichas correlacionan altamente entre sí.

C) Cuando tanto los predictores correlacionan muy altamente con las predichas, pero no así los predictores entre sí.

21. (TABLA 3) Indica el valor de la cuasidesviación típica:

A) 3’25

B) 3’32

C) 3’44

22. (TABLA 4) ¿Qué porcentaje de varianza de la variable “núm de casi-accidentes” explican los predictores “ri” y “c”:

A) 1’2%

B) 2’4%

C) 10’9%

23. (TABLA 4) ¿Qué predictores tienen una relación positiva con la variable predicha?:

A) Tanto “ri” como “c”

B) Únicamente “ri”

C) Ni “ri” ni “c”

24. Al efectuar transformaciones en la escalera de Tukey (v.g., raíz cuadrada, logaritmo):

A) Estamos cambiando la tendencia central, la variabilidad y la forma.

B) Estamos cambiando únicamente la tendencia central y la variabilidad, pero no la forma.

C) Estamos cambiando la forma, pero dejando intactas la tendencia central y la variabilidad.

Tabla 1.

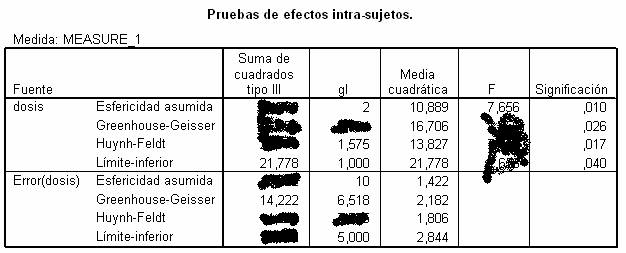
Tabla 2

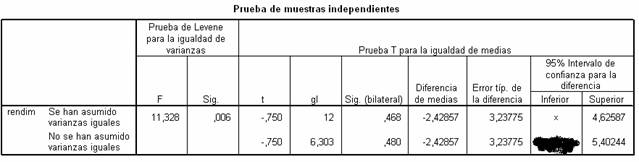
Tabla 3

datos Stem-and-Leaf Plot

Frequency Stem & Leaf

3,00 0 . 134

3,00 0 . 679

1,00 1 . 0

Stem width: 10

Each leaf: 1 case(s)

Tabla 4

Resumen del modelo

Modelo	R	R cuadrado	R cuadrado corregida	Error típ. de la estimación
1	,109(a)	$$$$$	$$$$$	1,44799

a Variables predictoras: (Constante), ri, c

Coeficientes(a)

Modelo		Coeficientes no estandarizados		Coeficientes estandarizados	t	Sig.
		B	Error típ.	Beta
1
	(Constant)	1,154	,455		2,538	,012
	c	-,156	,108	-,114	-1,442	,151
ri	,018	,146	,010	,121	,904

a Variable dependiente: número de casi-accidentes en ultimos 2 años