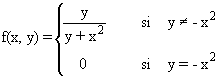
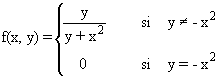
SOLUCIÓN:

El dominio de esta función es todo R² , ya que a todo punto (x,y) Î R² le hace corresponder un número real. El dominio, sin embargo está formado por la unión de dos subconjuntos según la imagen venga dada por una expresión analítica o por otra. Se estudiará la continuidad de la función en R² estudiando si la función lo es en cada uno de los dos conjuntos:
 

El primer subdominio, D₁, es un conjunto abierto al tratarse de la unión de dos conjuntos abiertos. Son conjuntos abiertos porque todos sus puntos son interiores (restricciones estrictas). Por este motivo, la imagen de los puntos que estén suficientemente próximos a cualquier punto de este subdominio vendrá dada por la misma expresión analítica que la que proporciona la imagen del punto al que están próximos. Es decir, se podrá encontrar, para cualquier punto de este subdominio, una bola centrada en ese punto que contendrá exclusivamente puntos de uno de los dos subconjuntos del primer subdominio, por lo que la imagen de los puntos de dicha bola vendrá dada por una única expresión analítica:
 

Esta expresión es el cociente de dos funciones reales de dos variables de tipo polinómico. Las funciones polinómicas son continuas en todos los puntos de su dominio, y el cociente de dos funciones (reales) continuas en un punto es otra función continua en ese punto, siempre que no se anule la función denominador en dicho punto. Por lo tanto, se puede concluir que la función f(x,y) es continua en todo punto (x,y) perteneciente al primer subdominio, pues no se anula el denominador:
 

El segundo subdominio, D₂, es un conjunto cerrado, al estar formado exclusivamente por los puntos frontera de dicho subdominio ( y = -x² ). Para estudiar la continuidad en este conjunto, se toma un punto que represente a todos los del subdominio, es decir, un punto indeterminado que satisfaga la(s) ecuación(es) o condición(es) de pertenencia al conjunto. Este punto podría ser el (x, -x² ), pues la segunda coordenada satisface la ecuación. Se tiene que la caracterización de una función continua en un punto de acumulación de su dominio implica que dicho punto admita imagen real, o sea, que pertenezca al dominio de la función, que exista el límite de la función al aproximarse a dicho punto y que el valor de la función en ese punto y el del límite coincidan.

La imagen para los puntos de este segundo subdominio es f(x, -x² ) = 0.

El límite de esta función hay que estudiarlo teniendo en cuenta que la función toma una expresión analítica al aproximarse al punto (x,-x² ) por puntos (x,y) que cumplan y = - x² diferente a la que toma al aproximarse por puntos (x,y) tales que cumplan y¹ -x² . Para que exista el límite doble deben existir los dos límites siguientes y coincidir:
 

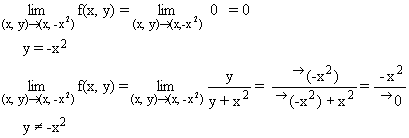
El primero vale 0. El segundo no existe si el punto de acumulación al que se tiende, (x,-x²), es un punto en que -x² ¹ 0, pues el numerador tendería a un valor finito, mientras que el denominador es un infinitésimo, lo que daría como resultado un infinito, ± ¥ . Así, se puede concluir que para los puntos (x, -x²) tales que -x²¹ 0 no existe el límite, por lo que la función no es continua en esos puntos. Si el punto de acumulación al que se tiende, (x, -x²), es un punto en que -x² = 0, el resultado del límite sería una indeterminación que habrá que resolver.

Si el punto (x, -x²), es un punto en que -x² = 0, resolviendo esta ecuación da como resultado x = 0, lo que se traduce en que el punto frontera que origina la indeterminación antes mencionada es el punto (0, 0).
 

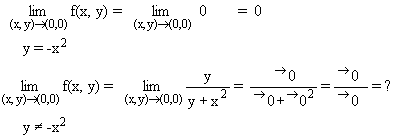
Planteando los límites iterados sobre este segundo límite, se tiene que:
 

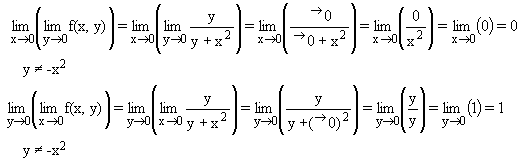
Como existen los dos, pero toman valores distintos (0 ¹ 1), se puede concluir que no existe el límite doble en el (0,0) y, por tanto, se puede concluir que la función no es continua en el (0,0).

NOTA: Se podía haber intentado resolver la indeterminación anterior haciendo un cambio a coordenadas polares. Como el punto de acumulación es el (0,0) el cambio es inmediato, no se requiere un cambio de variable previo. Lo que hay que señalar es que el cambio a coordenadas polares no evita que la función siga proporcionando imágenes a los puntos (x,y)Î R² mediante dos expresiones analíticas diferentes, según si los puntos son tales que y = -x² , o los puntos son tales que y ¹ -x² . El cambio a coordenadas polares es:
 

Planteando los límites queda:
 

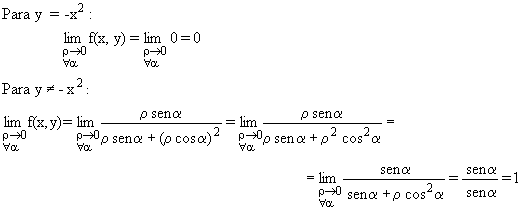
Da el mismo resultado, la inexistencia del límite doble (1¹ 0), y por tanto la no continuidad de la función en el (0,0).
 

La función es continua en:

La función no es continua " (x,y) Î { (x,y) Î R²/ y = -x² } .
 

2.- Estudie la continuidad de la siguiente función en R² :
 

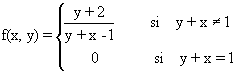
 SOLUCIÓN:

El dominio de esta función es todo R² , ya que a todo punto (x,y) Î R² , le hace corresponder un número real. El dominio, sin embargo es la unión de dos subconjuntos según la imagen venga dada por una expresión analítica o por otra. Se estudiará la continuidad de la función en R² estudiando si la función lo es en cada uno de los conjuntos:
 

El primer subdominio, D₁, es un conjunto abierto al ser la unión de dos conjuntos abiertos (todos sus puntos son interiores, las restricciones son estrictas). Por este motivo, la imagen de los puntos que estén suficientemente próximos a cualquier punto de D₁ vendrá dada por la misma expresión analítica que la que proporciona la imagen del punto al que están próximos. Es decir, se podrá encontrar, para cualquier punto de este subdominio, una bola centrada en ese punto que contendrá exclusivamente puntos del primer subdominio, por lo que la imagen de los puntos de dicha bola vendrá dada por una única expresión analítica:
 

Esta expresión es el cociente de dos funciones reales de dos variables de tipo polinómico (dos funciones lineales). Las funciones polinómicas son continuas en todos los puntos de su dominio, y el cociente de dos funciones (reales) continuas en un punto es otra función continua en ese punto, siempre que no se anule la función denominador en dicho punto. Por lo tanto, se puede aplicar estos resultados para concluir que la función f(x,y) es continua en todo punto (x,y) perteneciente al primer subdominio:
 

El segundo subdominio, D₂, es un conjunto cerrado al estar formado exclusivamente por los puntos frontera de dicho subdominio (y = 1-x). Para estudiar la continuidad en este conjunto, se toma un punto que represente a todos los del subdominio, es decir, un punto indeterminado que satisfaga la(s) ecuación(es) o condición(es) de pertenencia al conjunto. Este punto podría tomarse como el (x,1-x), pues la segunda coordenada, y, satisface la ecuación. La caracterización de una función continua en un punto de acumulación de su dominio implica que dicho punto admita imagen real (pertenezca al dominio de la función), que exista el límite de la función al aproximarse a dicho punto, y que el valor de la función en ese punto y el del límite coincidan.

La imagen para los puntos de este segundo subdominio es f(x, 1-x) = 0.

El límite de esta función habrá que estudiarlo teniendo en cuenta que la función proporciona una expresión analítica al aproximarse al punto (x,1-x) por puntos (x,y) que cumplan y=1-x diferente a la que resulta de aproximarse por puntos (x,y) que cumplan y+x¹ 1. Para que exista el límite doble deben existir los dos límites siguientes y coincidir:
 

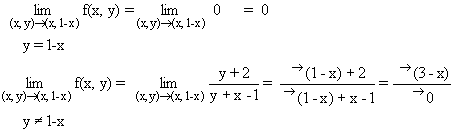
El primero vale 0. El segundo no existe si el punto de acumulación al que se tiende, (x,1-x), es un punto en que x¹ 3, pues el numerador tenderá a un valor finito, mientras que el denominador es un infinitésimo, lo que daría como resultado un infinito, ± ¥ . Así se puede concluir que para los puntos (x, 1-x) tales que x¹ 3 no existe el límite, por lo que la función no es continua en esos puntos.

Si el punto de acumulación al que se tiende, (x, 1-x), es un punto en que x = 3, el resultado del límite sería una indeterminación que habrá que resolver. Si el punto (x, 1-x), es un punto en que x = 3, resolviendo esta ecuación da como resultado un valor de 1-x = - 2, lo que se traduce en que el punto frontera que origina la indeterminación antes mencionada es el punto (3, -2).
 

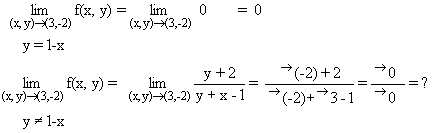
Planteando los límites iterados sobre este segundo límite, se tiene que:

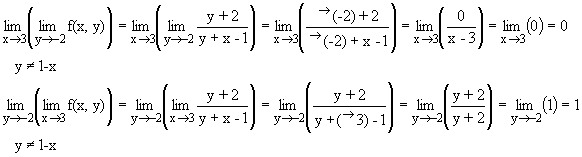
Como existen los dos, pero toman valores distintos (0 ¹ 1), se puede concluir que no existe el límite doble en el (3,-2), por lo que se puede concluir que la función no es continua en el (3,-2).

NOTA: Se podía haber intentado resolver la indeterminación haciendo un cambio a coordenadas polares (complicándose innecesariamente la resolución), pero como el punto de acumulación es el (3,-2) el cambio a polares no sería inmediato. Se requiere un cambio de variable previo. Lo que hay que señalar es que el cambio a coordenadas polares no evita que la función siga proporcionando imágenes a los puntos (x,y)Î R² mediante dos expresiones analíticas diferentes, según si los puntos son tales que y = 1-x, o los puntos son tales que y ¹ 1-x.

El cambio a coordenadas polares es:
 

Planteando los límites, queda:
 

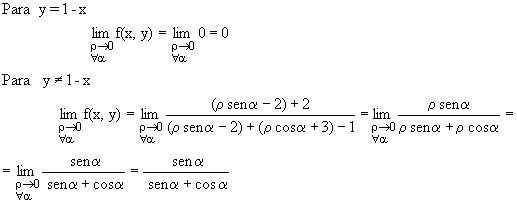
Da el mismo resultado, la inexistencia del límite doble, ya que el segundo no existe al depender su valor del ángulo a (tomará infinitos valores distintos según los tome a ), por tanto la función en el (3,-2) no será continua.

 RESUMEN DE RESULTADOS:
 

3.- Estudie la continuidad de la siguiente función en todo R² :
 

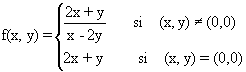
SOLUCIÓN:

El dominio de esta función no es todo R², ya que algún punto (x,y)Î R² no tiene asociada una imagen real por esta función. Esto sucede en puntos (x,y)Î R²/(x,y)¹ (0,0) con x-2y = 0, ya que anulan el denominador del cociente asociado a las imágenes de puntos distintos del (0,0). Como esos puntos no pertenecen al dominio de la función, ésta no es continua en esos puntos. Al (0,0) la función le hace corresponder la imagen 2x+y, es decir, f(0,0)= 2(0)+0 = 0. La función sí está definida en ese punto.

El dominio, está formado por la unión de dos subconjuntos según la imagen venga dada por una expresión analítica o por otra. Se estudiará la continuidad de la función en R² estudiando si la función lo es en cada uno de los dos conjuntos:
 

El primer subdominio es un conjunto abierto (unión de dos subconjuntos abiertos). Todos sus puntos son interiores (restricciones estrictas). Por este motivo, la imagen de los puntos que estén suficientemente próximos a cualquier punto de este subdominio vendrá dada por la misma expresión analítica que la que proporciona la imagen del punto al que están próximos. Es decir, se podrá encontrar, para cualquier punto de este subdominio, una bola centrada en ese punto que contendrá exclusivamente puntos del primer subdominio, por lo que la imagen de los puntos de dicha bola vendrá dada por una única expresión analítica:
 

Esta expresión es el cociente de dos funciones reales de dos variables de tipo polinómico. Las funciones polinómicas son continuas en todos los puntos de su dominio, y el cociente de dos funciones (reales) continuas en un punto es otra función continua en ese punto, siempre que no se anule la función denominador en dicho punto. Por lo tanto, se puede concluir que la función f(x,y) es continua en todo punto (x,y) perteneciente al primer subdominio, pues no se anula el denominador:
 

El segundo subdominio es un conjunto cerrado, al estar formado exclusivamente por el (0,0), punto frontera de dicho subdominio. El (0,0) es un punto de acumulación del dominio de la función, en toda bola centrada en el (0,0) se encontrarán siempre puntos del dominio distintos al (0,0). Este carácter, permite asegurar la continuidad en ese punto si existe la imagen y existe el límite de la función en dicho punto, y coinciden. Se sabe que f(0,0)= 0, por lo que resta estudiar el límite doble.

El límite de esta función habrá que estudiarlo teniendo en cuenta que la función toma la expresión analítica asociada a los puntos (x,y) ¹ (0,0) para puntos próximos a este último. En este caso, aproximarse al (0,0) sólo puede hacerse mediante puntos (x,y) que pertenezcan al primer subconjunto del dominio de la función. Se tiene que el límite se calcularía así:
 

Resulta una indeterminación a resolver. Planteando los límites iterados, se tiene:
 

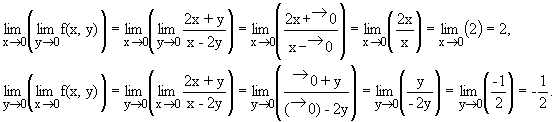
  Como existen los dos, pero toman valores distintos (2 ¹ -0’5), se puede concluir que no existe el límite doble en el (0,0) y que, por tanto, la función no es continua en el punto (0,0).

NOTA: Se podía haber intentado resolver la indeterminación, haciendo un cambio a coordenadas polares. Como el punto de acumulación es el (0,0) el cambio es inmediato, no se requiere un cambio de variable previo. El cambio a coordenadas polares es:
 

Planteando los límites, queda:
 

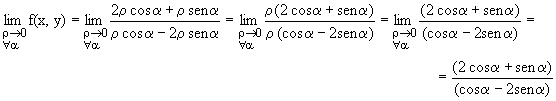
Depende del ángulo a , por lo que no existe el límite doble al no tomar un único valor. Daría el mismo resultado, la inexistencia del límite doble, y por tanto la no continuidad de la función en el (0,0).

RESUMEN DE RESULTADOS:

La función es continua en
 

4.- Estudie la continuidad de la siguiente función en todo R² :
 

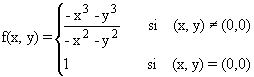
SOLUCIÓN:

El dominio de esta función es todo R², ya que todo punto (x,y)Î R² tiene asociada una imagen real por esta función. Para los puntos (x,y)Î R² / (x,y)¹ (0,0), la expresión de la función viene dada por un cociente cuyo denominador sólo se anula en el (0,0), por lo que todos los puntos distintos del (0,0) tendrán una imagen real dada por el cociente de dos polinomios, -(x³+y³) y -(x²+y²). Al (0,0) la función le hace corresponder la imagen de 1, es decir, f(0,0)= 1. La función sí está definida en ese punto. El dominio, está formado por la unión de dos subconjuntos según la imagen venga dada por una expresión analítica o por otra. Se estudiará la continuidad de la función en R² estudiando si la función lo es en cada uno de los dos conjuntos:
 

El primer subdominio es un conjunto abierto (unión de dos conjuntos abiertos, pues todos sus puntos son interiores, caracterizados por una restricción estricta). Por este motivo, la imagen de los puntos que estén suficientemente próximos a cualquier punto de este subdominio vendrá dada por la misma expresión analítica que la que proporciona la imagen del punto al que están próximos. Es decir, se podrá encontrar, para cualquier punto de este subdominio, una bola centrada en ese punto que contendrá exclusivamente puntos del primer subdominio, por lo que la imagen de los puntos de dicha bola vendrá dada por una única expresión analítica:
 

Esta expresión es el cociente de dos funciones reales de dos variables de tipo polinómico. Las funciones polinómicas son continuas en todos los puntos de su dominio, y el cociente de dos funciones (reales) continuas en un punto es otra función continua en ese punto, siempre que no se anule la función denominador en dicho punto. Por lo tanto, se puede concluir que la función f(x,y) es continua en todo punto (x,y) perteneciente al primer subdominio, pues no se anula el denominador:
 

El segundo subdominio es un conjunto cerrado, al estar formado exclusivamente por el (0,0), punto frontera de dicho subdominio. El (0,0) es un punto de acumulación del dominio de la función, en toda bola centrada en el (0,0) se encontrarán siempre puntos del dominio distintos al (0,0). Este carácter, permite asegurar la continuidad en ese punto si existe la imagen y existe el límite de la función en dicho punto, y coinciden. Se sabe que f(0,0)= 1, por lo que resta estudiar el límite doble.

El límite de esta función habrá que estudiarlo teniendo en cuenta que la función toma la expresión analítica asociada a los puntos (x,y) ¹ (0,0). En este caso, aproximarse al (0,0) sólo puede hacerse mediante puntos (x,y) que pertenezcan al primer subconjunto del dominio de la función. Se tiene que el límite se calcularía así:
 

Resulta una indeterminación a resolver. Planteando los límites iterados, se tiene:

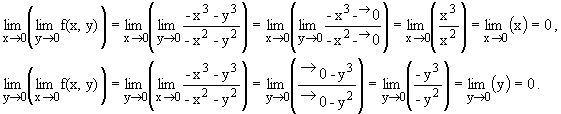
Como existen los dos y toman el mismo valor, 0, el límite doble no se puede asegurar que exista, pero si existe deberá tomar el valor de 0, y en ese caso no coincidiría con la imagen del (0,0), proporcionada por la función, f(0,0)=1, por lo que se puede concluir que la función no es continua en el (0,0).

NOTA: Se podía haber intentado resolver la indeterminación para conocer si existe o no el límite, haciendo un cambio a coordenadas polares, ya que el punto de acumulación es el (0,0) el cambio es inmediato, no se requiere un cambio de variable previo. El cambio a coordenadas polares es:
 

Planteando los límites, queda:

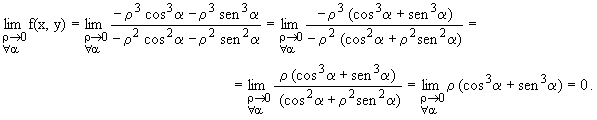
El límite existe y vale 0, pues (cos3a +sen3a ) está acotado "a , por lo que multiplicado por un infinitésimo el resultado tiende a 0. La conclusión sería la misma, aunque el límite doble existe y vale cero no coincide con f(0,0) que es 1, por tanto f no es continua en el (0,0).

RESUMEN DE RESULTADOS:

La función es continua en