1.- Obtenga razonadamente la dirección de máximo crecimiento en el punto (1,0,-1) de la función:
 

2.- Obtenga razonadamente la dirección de mínimo crecimiento (máximo decrecimiento) en el punto (-1,1,0) de la función:

a) Estudie la continuidad de la siguiente función en R².
b) ¿Es diferenciable en el (0,0)?
c) Obtenga, si es posible, la derivada direccional en el punto (0,0) en la dirección del vector (3,2).

a) Estudie la diferenciabilidad de la siguiente función en su dominio.
b) Obtenga la función derivada parcial respecto a x,

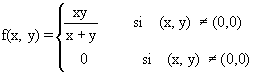
6.- Estudie la diferenciabilidad de la siguiente función en el punto (0,0) :
 

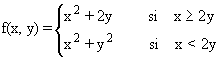
7.- Dada la siguiente función:
 

a) Estudie la diferenciabilidad de la siguiente función en su dominio.
b) Obtenga la dirección de máximo crecimiento en el punto (1,-2).

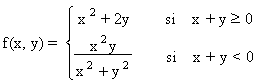
1.- Estudie la diferenciabilidad en el punto (1,1) de:
 

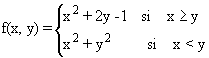
SOLUCIÓN:

El dominio de la función f(x,y) es todo R² , aunque resulta de la unión de dos subconjuntos D_f={(x,y)Î R²/ x ³ y} È { (x,y)Î R²/ x < y} . El punto (1,1), pues, es un punto frontera de esos dos subconjuntos (x = y).

Para que f(x,y) sea diferenciable en el (1,1) debe ser continua y derivable en dicho punto, condiciones necesarias de diferenciabilidad en un punto. Si no es continua en el (1,1) se puede concluir que no será diferenciable en el (1,1). Ya que el (1,1) es un punto de acumulación del dominio de esta función, al ser un punto interior del dominio, R² , la continuidad en ese punto se justifica si existe la imagen y existe el límite de la función en dicho punto, y coinciden.
 

Como el (1,1) es un punto frontera de los dos subdominios, en cualquier bola centrada en dicho punto se encontrarán puntos del primer subconjunto y puntos del segundo subconjunto, lo que hay que tener en cuenta al calcular el límite de la función. Así, se va a tratar de determinar a qué valor se aproximan las imágenes de los puntos próximos al (1,1) que pertenezcan al primer subconjunto y, por otra parte, a qué valor se aproximan las imágenes de los puntos próximos al (1,1) que pertenezcan al segundo subconjunto. Ambos valores deben existir y coincidir para concluir que el límite doble existe y toma ese único valor.
 

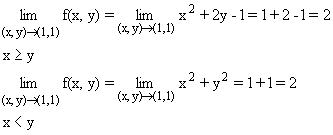
Como coinciden los valores, se puede concluir que el límite doble existe y vale 2, lo mismo que f(1,1), por tanto la función es continua en el (1,1). Todavía no se sabe si es o no es diferenciable en dicho punto.

Ahora, se va a estudiar la derivabilidad (existencia de todas las derivadas parciales).
 

(*) Como f tiene el dominio constituido por la unión de dos subconjuntos, f(1+h,1) dependerá del signo de h, de tal manera que si h >0 ® 1+h >1, por lo que (1+h,1) pertenecerá al primer subdominio; mientras que si h<0 ® 1+h < 1, (1+h,1) pertenecerá al segundo subdominio.
 

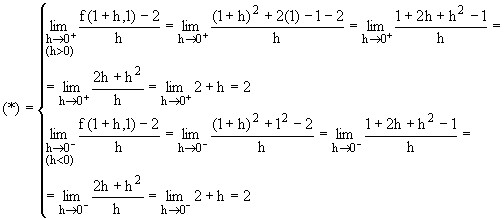
 Como existen y coinciden los dos, se puede concluir que
 

(*) Como f tiene el dominio constituido por la unión de dos subconjuntos, f(1,1+h) dependerá del signo de h, de tal manera que si h>0 ® 1<1+h, por lo que (1,1+h) pertenecerá al segundo subdominio, mientras que si h<0 ® 1>1+h, (1,1+h) pertenecerá al primer subdominio.
 

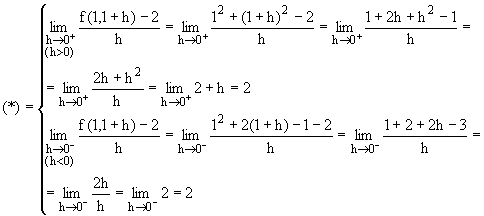
Como existen y coinciden los dos, se puede concluir que
 

Como existen las dos derivadas parciales, f es derivable en el (1,1), pero todavía no se sabe si es diferenciable. Se va a proceder a comprobarlo con la definición de diferenciabilidad en un punto. La función f será diferenciable si el límite siguiente existe y toma el valor de 0.
 

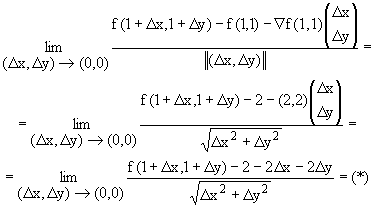
(*) Como f tiene el dominio constituido por la unión de dos subconjuntos, f(1+D x,1+D y) dependerá de D x y de D y. Si D x ³ D y ® 1+D x ³ 1+D y, por lo que (1+D x,1+D y) pertenecerá al primer subdominio, mientras que si D x <D y® 1+D x < 1+D y, (1+D x,1+D y) pertenecerá al segundo subdominio. Habrá que desdoblar el límite anterior, debiendo existir y valer 0 en los dos casos para que f sea diferenciable en el (1,1).
 

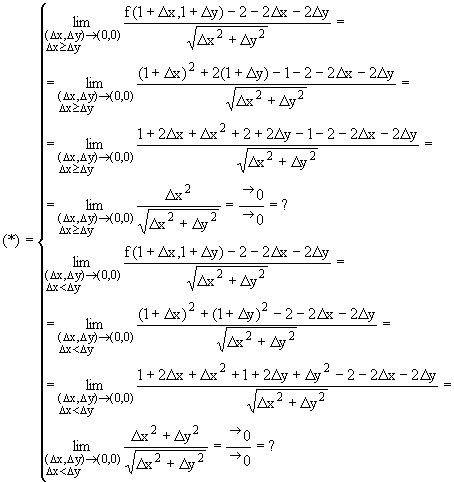
Resolviendo las indeterminaciones para los dos casos mediante un cambio a coordenadas polares, se tiene:
 

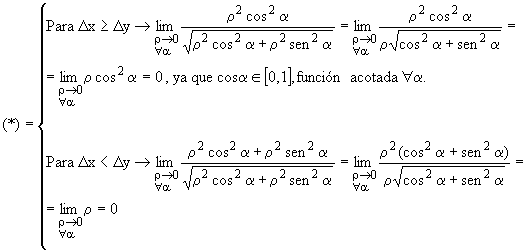
Por tanto, como existen los dos y coinciden con 0, el límite doble existe y vale 0, lo que permite concluir que la función es diferenciable en el (1,1).

2.- Estudie la diferenciabilidad de la siguiente función en el punto (1,1):
 

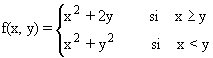
SOLUCIÓN:

El dominio de la función f(x,y) es todo R² , aunque resulta de la unión de dos subconjuntos D_f={(x,y)Î R²/ x ³ y} È { (x,y)Î R²/ x < y} . El punto (1,1), pues, es un punto frontera de esos dos subconjuntos (x = y).

Para que f(x,y) sea diferenciable en el (1,1) debe ser continua y derivable en dicho punto. Si no es continua en el (1,1) se puede concluir que no es diferenciable en el (1,1).

Ya que el (1,1) es un punto de acumulación del dominio de esta función, al ser un punto interior del dominio, la continuidad en ese punto se justifica si existe la imagen y existe el límite de la función en dicho punto, y coinciden.
 

Como el (1,1) es un punto frontera de los dos subdominios, en cualquier bola centrada en dicho punto se encontrarán puntos del primer subconjunto y puntos del segundo subconjunto, lo que hay que tener en cuenta al calcular el límite de la función. Así, se va a tratar de determinar a qué valor se aproximan las imágenes de los puntos próximos al (1,1) que pertenezcan al primer subconjunto y, por otra parte, a qué valor se aproximan las imágenes de los puntos próximos al (1,1) que pertenezcan al segundo subconjunto. Ambos valores deben existir y coincidir para concluir que el límite doble existe y toma ese único valor.
 

Como no coinciden los valores, se puede concluir que el límite doble no existe y por tanto la función no es continua en el (1,1), por lo que no es diferenciable en dicho punto.

3.- Obtenga la dirección de máximo crecimiento en el punto (1,0,-1) de la función:
 

SOLUCIÓN:

La función f(x,y,z) es una función diferenciable en todos los puntos de su dominio al tratarse de la suma de una función polinómica más el producto de una trigonométrica por una exponencial, siendo todas ellas derivables en R³, las funciones resultantes de esas operaciones también lo serán. Dado que la función es diferenciable, no hay ningún problema en afirmar que la dirección de máximo crecimiento, en referencia a la derivada direccional, la indica el vector gradiente de la función en el punto (1, 0, -1). Primero se va a obtener el vector gradiente en un punto (x,y,z) cualquiera y después se procederá a sustituir el punto en cada una de las tres derivadas parciales. Se aplican, pues, las reglas de derivación para obtener las derivadas parciales de f.
 

El vector (-4,3,-4) indica la dirección de máximo crecimiento en el punto (1,0-1).

4.- Obtenga la dirección de mínimo crecimiento o de máximo decrecimiento en el punto (-1,1,0) de la función:
 

SOLUCIÓN:

La función f(x,y,z) es una función diferenciable en todos los puntos de su dominio al tratarse de la suma de una función polinómica más el producto de una trigonométrica por una exponencial, como todas estas son diferenciables en R³, las funciones resultantes de esas operaciones también lo serán. Dado que la función es diferenciable, no hay ningún problema en afirmar que la dirección de máximo decrecimiento o crecimiento mínimo, en referencia a la derivada direccional, la indica el vector opuesto al vector gradiente de la función en el punto (-1, 1, 0). Primero se va a obtener el vector gradiente en un punto (x,y,z) cualquiera y después se procederá a sustituir el punto en cada una de las tres derivadas parciales. Por último, para obtener el vector opuesto al gradiente se multiplicará éste por menos uno. Se aplican, pues, las reglas de derivación para obtener las derivadas parciales de f.
 

El vector (4,4,-3) indica la dirección de mínimo crecimiento en el punto (-1,1,0).