Tena 4

TEMA 4.- MODELOS BÁSICOS DE PL. PNL APROXIMABLE MEDIANTE PL Y PEM

Bibliografía: El tema se puede seguir en la sección 1.5 del capítulo 1 y en el capítulo 3 del libro de prácticas, "Modelización y resolución de problemas de optimización en Economía".

Modelos básicos de Programación Lineal. (Sección 1.5)

Combinación óptima de recursos.
Problemas de mezcla.
Selección de procesos.
Modelos de optimización en redes y combinatoria:

Modelo de transporte.
Modelo de transbordo.
Modelo de asignación.
Flujo con coste mínimo en una red.
Camino más corto en una red.

Transformaciones de problemas no lineales y/o no diferenciables a Programación lineal:

No linealidades aparentes: ejemplo 3.1.

Un ejemplo del primer caso se puede ver en el problema de determinación de la mezcla que minimiza el coste de la producción de gasolina. La gasolina súper se obtiene mezclando butano, reformado catalítico y nafta. La mezcla debe cumplir unas características de octanaje, presión de vapor y volatilidad. El coste de cada input y su contribución, en términos de cada una de las características, se ven en la siguiente tabla:

	Producto
Característica/litro	Butano	Reformado catalítico	Nafta	Requerimiento
Octanaje	120	100	74	³ 94
Presión de vapor	60	2’6	4’1	£ 11
Volatilidad	105	3	12	£ 17
Coste/Unidad	1000	2700	1800	-

La característica que aporta cada input al producto final, gasolina súper, se consigue en función de la participación en tanto por uno del input sobre el producto final, por ejemplo, si se emplea un litro de butano por litro de gasolina se tendrían los 120 octanos que proporciona el butano según la tabla.

Además, se debe producir un mínimo de 8.000 litros de gasolina y se dispone como mucho de 1.000 unidades (litros) de butano. Se desea hallar la mezcla que cumpla todas las especificaciones y minimice los costes. La formulación matemática quedaría:

Min C(x_BUT, x_REF, x_NAF) = 1000 x_BUT + 2700 x_REF + 1800 x_NAF

sujeto a:

Especificaciones de calidad (características):

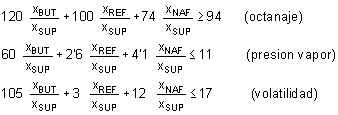
Ecuación de balance (Al no existir pérdidas de ninguno de los componentes en la mezcla, la suma de los inputs debe coincidir con la cantidad de producto final):

x_BUT + x_REF + x_NAF = x_SUP

Disponibilidad de butano

x_BUT £ 1000

Demanda de gasolina súper

x_SUP ³ 8000

No negatividad de las variables:

x_BUT, x_REF, x_NAF, x_SUP ³ 0

Las inecuaciones referentes a las especificaciones de calidad no son lineales, sin embargo se pueden linealizar multiplicando por x_SUP que es no negativa, quedando tres desigualdades lineales:

120 x_BUT + 100 x_REF + 74 x_NAF -94 x_SUP ³ 0

60 x_BUT + 2’6 x_REF + 4’1 x_NAF -11 x_SUP £ 0

105 x_BUT + 3 x_REF + 12 x_NAF -17 x_SUP £ 0

Obteniendo, pues, un programa lineal.

Deseconomías a escala: Maximización de funciones con rendimientos decrecientes o minimización de funciones con rendimientos crecientes (epígrafe 3.2.1): precios de venta decrecientes por tramos (ejemplo 3.2) o costes de producción crecientes por tramos.
Optimización de funciones de coeficientes fijos (epígrafe 3.2.2): funciones de utilidad de bienes perfectamente complementarios (ejemplo 3.3) o funciones de producción con factores perfectamente complementarios.
Problemas multiobjetivo (epígrafe 3.2.3): una forma de abordar el problema consiste en maximizar el mínimo valor de los objetivos (cuando todos se quieren maximizar) o en minimizar el máximo valor de los objetivos (cuando todos se quieren minimizar). La primera estrategia se llama maximín (ejemplo 3.4) y la segunda minimax.
Problemas de programación lineal fraccional (epígrafe 3.2.4): cuando la función objetivo es el cociente de funciones lineales existe un cambio de variables estándar que transforma el problema en lineal (ejemplo 3.5).

Transformaciones de problemas no lineales y/o no diferenciables a Programación entera mixta:

Problemas de carga fija (epígrafe 3.3.1): se introduce una variable binaria para indicar si se lleva a cabo o no la actividad (ejemplo 3.6).
Problemas de lotes (epígrafe 3.3.2) o con variables semicontinuas: se introduce una variable binaria para indicar si la variable se encuentra en el punto de discontinuidad o en la región de continuidad (ejemplo 3.7).
Economías a escala: Maximización de funciones con rendimientos crecientes o minimización de funciones con rendimientos decrecientes (epígrafe 3.3.3): precios de venta crecientes por tramos o costes de producción decrecientes por tramos, bien de forma discreta (ejemplo 3.8) o bien de forma continua (ejemplo 3.9).
Problemas con la función valor absoluto (epígrafe 3.3.4): se realiza una transformación estándar (ejemplo 3.10).

Inicio

Atrás