TEMA 2.- ANÁLISIS CONVEXO
2.1.- Convexidad de conjuntos.
2.1.1.- Nociones previas.
-
Recta.
-
Semirecta.
-
Segmento Lineal Cerrado.
-
Segmento Lineal Abierto.
2.1.2.- Concepto de conjunto convexo.
2.1.3.- Propiedades de los conjuntos convexos.
-
El vacío, Rn, y los conjuntos formados por un solo punto
son convexos.
-
La intersección de convexos es convexa.
-
La combinación lineal de conjuntos convexos es un conjunto convexo.
-
El producto cartesiano de conjuntos convexos es un conjunto convexo.
-
La imagen de un conjunto convexo en una aplicación lineal es también
un conjunto convexo.
2.1.4.- Hiperplanos, semiespacios y otros conjuntos convexos.
-
Hiperplano.
-
Semiespacios.
-
Polítopos.
-
Poliedro.
-
Punto extremo.
-
Hiperplano acotador.
2.1.5.- Conceptos y teoremas sobre hiperplanos de separación
e hiperplanos soporte.
-
Hiperplano de separación.
-
Hiperplano de separación estricta.
-
Separación entre un punto y un conjunto.
-
Teorema de separación de conjuntos convexos de Minkowski.
-
Hiperplano soporte.
-
Teorema del hiperplano soporte.
-
Hiperplano tangencial.
-
Condición suficiente de existencia de punto extremo.
-
Arista.
-
Arista infinita.
2.1.6.- Envoltura convexa.
-
Combinación lineal convexa.
-
Condición necesaria y suficiente de conjunto convexo.
-
Envoltura convexa.
-
Convexificación de un conjunto.
-
Caracterización de la envoltura convexa.
-
Teorema de Caratheodory.
-
Teorema de representación de Minkowski.
2.2.- Convexidad de funciones.
2.2.1.- Conceptos y relaciones inmediatas.
-
Funciones cóncavas.
-
Función convexa.
-
Función estrictamente cóncava.
-
Función estrictamente convexa.
2.2.2.- Propiedades.
-
f estrictamente cóncava ® f cóncava
-
f cóncava « - f convexa
-
S convexo, no vacío; f continua en S y cóncava en Int(S)
®
f cóncava en S
-
La combinación lineal no negativa de funciones cóncavas es
otra función cóncava.
-
La función mínimo de un conjunto de funciones cóncavas
es una función cóncava.
-
Desigualdad de Jensen: Una función es cóncava en S, si y
sólo si la imagen de toda combinación lineal convexa de más
de un punto de dicho conjunto S es mayor o igual que la combinación
lineal convexa de las imágenes de esos puntos con los mismos coeficientes.
2.2.3.- Caracterizaciones de la concavidad y de la convexidad.
-
Caracterización gráfica:
-
Grafo, epígrafo, hipógrafo.
-
Caracterización: f cóncava «
hf convexo
-
Caracterización por conjuntos de nivel:
-
Conjunto de nivel, de nivel superior, de nivel inferior.
-
Caracterización: f cóncava en S ®
Sa convexo " a.
-
Caracterización de funciones de clase C1 en S abierto,
convexo y no vacío:
f cóncava en S « (x-x0)tÑ
f(x0)³ f(x)-f(x0)
"
x0, xÎ S
-
Caracterización de funciones de clase C2 en S abierto,
convexo y no vacío:
-
f cóncava en S « Hf(x) "SDN" "
xÎ S.
-
f convexa en S « Hf(x) "SDP" "
xÎ S.
-
Hf(x) DN " xÎ
S ® f estrictamente cóncava en S.
-
Hf(x) DP " xÎ
S ® f estrictamente convexa en S.
-
Caracterización según el grado de homogeneidad (cond. necesaria):
f: Rn++® R++
homogénea de grado r:
-
Si f es cóncava ® rÎ
[
0,1]
-
Si f es convexa ® r £
0, ó r ³ 1.
2.2.4.- Concavidad y convexidad de funciones compuestas.
-
Función no decreciente, función creciente, función
no creciente, función decreciente.
-
Condición suficiente de concavidad (convexidad) de la función
compuesta:
-
f cóncava, g cóncava y no decreciente ®
F = g° f = g[
f(x)] es cóncava.
-
f convexa, g convexa y no decreciente ®
F = g° f = g[
f(x)] es convexa.
-
Función indirectamente cóncava o concavificable
2.2.5.- Análisis convexo en optimización.
-
Máximo f(x) « Mínimo -f(x).
-
Optimización de funciones compuestas F(x)=g[f(x)]:
-
g no decreciente, x* máximo de f en S ®
x* máximo de F sobre S.
-
g creciente, x* máximo de f en S «
x* máximo de F sobre S.
-
Teorema local-global.
2.3.- Extensiones de la convexidad en conjuntos.
2.3.1.- Conjuntos estrictamente convexos.
-
Definición.
-
Conjunto estrictamente estrictamente convexo en un punto frontera.
-
Aplicaciones.
2.3.2.- Conos convexos.
-
Rayo.
-
Cono.
-
Cono convexo.
-
Condición necesaria y suficiente de cono convexo.
-
Envoltura cónica.
-
Menor cono convexo.
-
Cono normal o polar.
-
Cono dual.
-
Propiedades de los conos convexos duales.
2.4.- Extensiones de la convexidad en funciones.
2.4.1.- Funciones pseudocóncavas y pseudoconvexas.
Definiciones.
Propiedades.
DEFINICIONES:
-
Función pseudocóncava.
-
Función estrictamente pseudocóncava.
-
Función pseudocóncava localmente en un punto.
-
Función estrictamente pseudocóncava localmente en un punto.
-
Función (estric.) pseudomonotónica.
PROPIEDADES:
-
f (estrict.) pseudocóncava sobre S si y sólo si f es (estric.)
pseudocóncava localmente "xÎS.
-
f (estric.) pseudoconvexa « -f (estric.)
pseudocóncava.
-
f estrict. pseudocóncava (pseudoconvexa) en S ®
f pseudocóncava (pseudoconvexa) en S.
-
f (estric.) cóncava (convexa) en S ®
f (estric.) pseudocóncava (pseudoconvexa) en S.
-
f pseudocóncava (psudoconvexa) ®
continuidad.
-
f (estric.) pseudocóncava (pseudoconvexa) sobre S ®
1/f (estric.) pseudoconvexa (pseudocóncava) sobre S.
-
En una función pseudocóncava (pseudoconvexa) no existen planos
tangentes horizontales en puntos que no sean máximo (mínimo)
global.
2.4.2.- Caracterización de funciones pseudocóncavas
y pseudoconvexas.
-
Caracterización gráfica.
-
Caracterización por conjuntos de nivel.
-
Caracterización de clase C2:
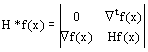 CONDICIONES SUFICIENTES:
CONDICIONES SUFICIENTES:
-
Por menores principales de H*f(x), hr*:
(-1)r hr* ³
0 con (-1)r hr ³
0 si hr* = 0, " xÎ
S, " rÎ {1,¼
,n}
¯
f pseudocóncava.
(-1)r hr* ³ 0
con (-1)r hr > 0 si hr* = 0, "
xÎ S, " rÎ
{1,¼ ,n}
¯
f estrictamente pseudocóncava.
hr* £ 0 con hr
³
0 si hr* = 0, " xÎ
S, " rÎ {1,¼
,n}
¯
f pseudoconvexa.
hr* £ 0 con hr
> 0 si hr* = 0, " xÎ
S, " rÎ {1,¼
,n}
¯
f estrictamente pseudoconvexa.
-
Por menores principales conducentes de H*f(x), Hr*:
(-1)rHr*>0, "
xÎ S," rÎ
{1,¼ ,n}®
f estric. pseudocóncava.
Hr* < 0, " xÎ
S, " rÎ {1,¼
,n}® f estric. pseudoconvexa.
2.4.3.- Pseudoconcavidad y pseudoconvexidad de funciones compuestas.
Dada la función compuesta de dos funciones diferenciables,
F(x)=g[f(x)], definida en S:
-
f (estric.) pseudocóncava (pseudoconvexa) y g no decreciente ®
F pseudocóncava (pseudoconvexa) sobre S.
-
f estric. pseudocóncava (pseudoconvexa) y g creciente ®
F estrict. pseudocóncava (pseudoconvexa) sobre S.
2.4.4.- Funciones cuasicóncavas y cuasiconvexas. Definiciones
y propiedades.
DEFINICIONES:
-
Función cuasicóncava.
-
Función estrictamente cuasicóncava. (Función cuasicóncava
fuerte o semiestric. cuasicóncava).
-
Función explícitamente cuasicóncava.
-
Función cuasicóncava localmente en un punto.
-
Función estrictamente cuasicóncava localmente en un punto.
-
Función explícitamente cuasicóncava localmente en
un punto.
-
Función (estric.) cuasimonotónica.
PROPIEDADES:
-
f (estric.) cuasiconvexa « -f (estric.)
cuasicóncava.
-
f, función real de variable real no decreciente o no creciente en
S ®f cuasimonotónica en S.
-
f, función real de variable real creciente o decreciente en S®f
estrictamente cuasimonotónica en S.
-
f estrict. cuasicóncava (cuasiconvexa) en S ®
f explícitamente cuasicóncava y cuasicóncava (cuasiconvexa)
en S.
-
f explícitamente cuasicóncava (cuasiconvexa) en S ®
f cuasicóncava (cuasiconvexa) en S.
-
f (estric.) cóncava (convexa) ® f
(estric.) cuasicóncava (cuasiconvexa).
-
f cóncava (convexa) ® f explícitamente
cuasicóncava (cuasiconvexa).
-
f (estric.) pseudocóncava (pseudoconvexa) ®
f (estric.) explícitamente cuasicóncava (cuasiconvexa).
-
f continua en S convexo y no vacío, y f cuasicóncava (cuasiconvexa)
en Int(S) ® f cuasicóncava (cuasiconvexa)
en todo S.
-
f (estric.) cuasicóncava (cuasiconvexa) positiva o negativa sobre
S (convexo y no vacío), es decir f(S)Ì
R++ ó f(S)Ì R--
®
f-1= 1/f, es (estric.) cuasiconvexa (cuasicóncava) sobre
S.
2.4.5.- Caracterización de funciones cuasicóncavas
y cuasiconvexas.
-
Caracterización gráfica:
-
Hf (Ef) convexo ®
f cuasicóncava (cuasiconvexa) en S.
-
Caracterización por conjuntos de nivel:
-
f cuasicóncava (cuasiconvexa) sobre S «
Sa (Sa) convexo " aÎ
R.
-
f estrict. cuasicóncava (cuasiconvexa) sobre S ®
Sa
(Sa) estrict. convexo"aÎR.
-
Caracterización de clase C1:
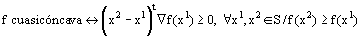
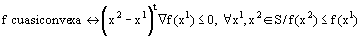
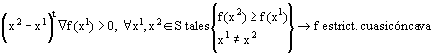
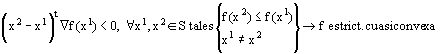
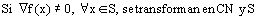
CONSECUENCIAS CARACT. C1:
-
f (estr.) pseudocóncava (pseudoconvexa) en S abierto, convexo y
no vacío ® f (estr.) cuasicóncava
(cuasiconvexa) en S.
-
f pseudocóncava (pseudoconvexa) y estrict. cuasicóncava (cuasiconvexa)
en S abierto, convexo y no vacío ®
f estr. pseudocóncava (pseudoconvexa) en S.
-
f diferenciable, no estacionaria y (estr.) cuasicóncava (cuasiconvexa)
en S abierto, convexo y no vacío ®
f (estr.) pseudocóncava (pseudoconvexa) en S.
-
Sa (Sa) estrictamente convexo "
aÎ R, f diferenciable y no estacionaria
en S abierto, convexo y no vacío ®
f estrict. pseudocóncava (pseudoconvexa) y cuasicóncava (cuasiconvexa)
sobre S.
-
Caracterización de clase C2, por menores principales
de H*, hr*:
CONDICIÓN NECESARIA:
f cuasicóncava en S ® (-1)r
hr* ³ 0, "
xÎ S, " rÎ
{
1,¼ ,n}
f cuasiconvexa en S ® hr*
£
0, " xÎ S,
" rÎ {
1,¼ ,n}
CONDICIÓN SUFICIENTE:
(-1)rHr*>0," xÎ
S," rÎ {
1,¼ ,n} ®
f estr. cuasicóncava en S
Hr*< 0," xÎ
S," rÎ {
1,¼ ,n} ®
f estr. cuasiconvexa en S
2.4.6.- Cuasiconcavidad y cuasiconvexidad de funciones compuestas
y homogéneas.
Dada la función compuesta de dos funciones diferenciables,
F(x)=g[f(x)], definida en S, convexo y no vacío:
-
f cuasicóncava (cuasiconvexa) y g no decreciente ®
F cuasicóncava (cuasiconvexa) sobre S.
-
f estrict. cuasicóncava (cuasiconvexa) y g creciente (decreciente)
®
F estrict. cuasicóncava (cuasiconvexa) sobre S.
-
f cuasicóncava (cuasiconvexa) y g no creciente ®
F cuasiconvexa (cuasicóncava) sobre S.
-
f estrict. cuasicóncava (cuasiconvexa) y g decreciente (creciente)
®
F estrict. cuasiconvexa (cuasicóncava) sobre S.
-
f cóncava (convexa) y estrict. cuasicóncava (cuasiconvexa)
y g no decreciente y estrict. cóncava (convexa) ®
F estrict. cóncava (convexa).
-
Para f:Rn++® R++,
fÎ C1 y homogénea de
grado r=1, f cóncava (convexa) «
f cuasicóncava (cuasiconvexa).
-
Para f:Rn++® R+,
fÎ C1 y homogénea de
grado rÎ (0,1]
=1, f cóncava (convexa) « f cuasicóncava
(cuasiconvexa).
-
Ejemplo Cobb-Douglas.
2.4.7.- Análisis convexo generalizado en optimización.
-
Si f es pseudocóncava (pseudoconvexa) en S convexo, abierto y no
vacío de Rn y x*Î S
tal que Ñ f(x*)=q
®
x* máximo (mínimo) global de f en S.
-
Si f estrict. pseudocóncava (pseudoconvexa) en S convexo, abierto
y no vacío de Rn y x*Î
S tal que Ñ f(x)=q
"xÎS®
existe solución única de Ñ
f(x)=q , x*, que es máximo (mínimo)
global único f en S.
-
Teorema local-global para cuasiconcavidad: f:S®
R con S convexo y no vacío:
-
f cuasicóncava (cuasiconvexa), x*Î
S máximo (mínimo) local único ®
x* máximo (mínimo) global.
-
f explícitamente cuasicóncava (cuasiconvexa), x*Î
S máximo (mínimo) local ®
x* máximo (mínimo) global.
-
f estrictamente cuasicóncava (cuasiconvexa), x*Î
S máximo (mínimo) local único ®
x* máximo (mínimo) global único.
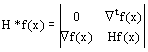
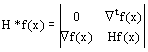
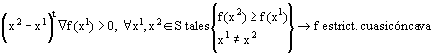
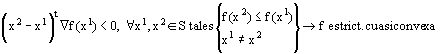
![]()