AMPLIACIÓ DE MÈTODES NUMÈRICS – Enginyeria Química – curs 2006-2007
Exercici 1:
Calcular analíticament la solució del sistema d'equacions {x2+y2=1, x2-y2=0'5}. Obtenir i simplificar les expressions per a la seua aproximació pel mètode de Newton. Obtenir el Jacobià del sistema i estudiar la zona de convergència d'aquest mètode. Aplicar-ho a partir del punt (1,3).
Exercici 2:
Resoldre el sistema d'equacions
10 x1 + 5x2 + 2x3 = 3
0'1x1 + 2x2 + x3 = 1
3x1 + 2x2 + 6x3 = 2
per eliminació gaussiana i per descomposició LU; comprovar que els dos mètodes són algebraicament equivalents i es realitzen les mateixes operacions aritmètiques.
Exercici 3:
1) Obtenir, utilitzant l'algoritme 3, els valors i vectors propis de
A =![]()
2) Obtenir una aproximació al valor propi d'A amb màxim valor absolut utilitzant l'algoritme 4 amb
p(0)=![]() i
ε=0'1
i
ε=0'1
Obtenir els discs de Gerschgorin per a A i comprobar que tot valor propi està dins d'un disc i que una unió connexa de 2 discs conté exactament 2 valors propis.
(veure http://cellular.ci.ulsa.mx/comun/jesus/node29.html i http://www.maths.uq.edu.au/~asj/LINALG/gersch.pdf )
Exercici 4:
Reduit a una matriu semblant de Hessenberg superior, utilitzant l'algoritme 8, les matrius:
a)
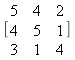 b)
b)
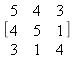
Aplicar l'algoritme 9 per a reduir la matriu de l'apartat (b) a una matriu semblant tridiagonal, i comprobar que s'obté el mateix resultat que amb l'algoritme 8.
Exercici 5:
Resoldre el sistema d'equacions normals per a obtenir la millor aproximació f* a f(x)=x2+x+1dins del subespai definit per les funcions base φ0(x)=1, φ1(x)=x,
a) amb la distància definida pel producte escalar discret en els nodos x0=-1, x1=0, x2=1 .
b) amb la distància definida pel producte escalar continu en l'interval [-1,1] .
Calcular en ambdós casos el residu ||f-f*||2 .
c) Intentar obtenir la millor aproximació f* dins del subespai anterior resolent el sistema Ma*=y, amb Mkj=φj(xk), yk=f(xk) amb la funció anterior i amb la funció f(x)=sin(πx/2)+cos(πx/2)+x2 . Calcular en el seu cas el residu ||f-f*||2 amb el producte escalar discret en els nodos de l'apartat (a)