 Actividad
4:
Actividad
4:
 Actividad
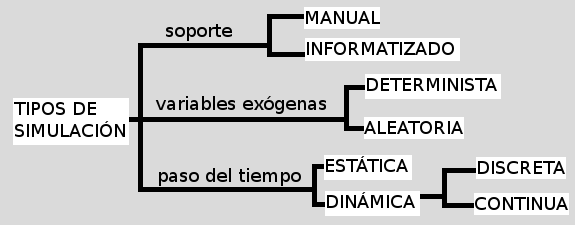
4: Atendiendo al tipo de soporte utilizado, a la
información de que se dispone sobre las variables
exógenas y a la
consideración, en su caso, del paso del tiempo, poner
ejemplos de
simulaciones de distintos tipos. Comenzar clasificando las simulaciones
tratadas en las actividades anteriores, y añadir otros
ejemplos hasta
completar los doce tipos de simulaciones posibles.
Actividad
4: Atendiendo al tipo de soporte utilizado, a la
información de que se dispone sobre las variables
exógenas y a la
consideración, en su caso, del paso del tiempo, poner
ejemplos de
simulaciones de distintos tipos. Comenzar clasificando las simulaciones
tratadas en las actividades anteriores, y añadir otros
ejemplos hasta
completar los doce tipos de simulaciones posibles.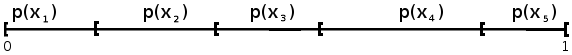 , y para cada
término
de la SPA en [0, 1[ tomamos el valor x de la
variable X
correspondiente al segmento en el que se encuentre dicho
término.
, y para cada
término
de la SPA en [0, 1[ tomamos el valor x de la
variable X
correspondiente al segmento en el que se encuentre dicho
término. 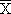 -μ)/σ(
-μ)/σ(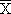 ) ,
) ,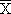 es la media de los resultados obtenidos,
es la media de los resultados obtenidos,
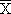 )=√(∑ i=1
N (Xi-
)=√(∑ i=1
N (Xi-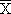 )2/(N·(N-1)))
es el valor estimado de la desviación típica de las medias, y
)2/(N·(N-1)))
es el valor estimado de la desviación típica de las medias, y TABLA INVERSA DE LA DISTRIBUCION t de Student (calculada con octave):donde el parámetro ν=N-1 recibe el nombre de grados de libertad de la distribución, y p es la probabilidad acumulada (ver figura). Si ν>40ν |p 0.60 0.70 0.75 0.80 0.85 0.90 0.95 0.99 0.995
----------------------------------------------------------------------------
1 | 0.325 0.727 1.000 1.376 1.963 3.078 6.314 31.821 63.657
2 | 0.289 0.617 0.816 1.061 1.386 1.886 2.920 6.965 9.925
3 | 0.277 0.584 0.765 0.978 1.250 1.638 2.353 4.541 5.841
4 | 0.271 0.569 0.741 0.941 1.190 1.533 2.132 3.747 4.604
5 | 0.267 0.559 0.727 0.920 1.156 1.476 2.015 3.365 4.032
6 | 0.265 0.553 0.718 0.906 1.134 1.440 1.943 3.143 3.707
7 | 0.263 0.549 0.711 0.896 1.119 1.415 1.895 2.998 3.499
8 | 0.262 0.546 0.706 0.889 1.108 1.397 1.860 2.896 3.355
9 | 0.261 0.543 0.703 0.883 1.100 1.383 1.833 2.821 3.250
10 | 0.260 0.542 0.700 0.879 1.093 1.372 1.812 2.764 3.169
11 | 0.260 0.540 0.697 0.876 1.088 1.363 1.796 2.718 3.106
12 | 0.259 0.539 0.695 0.873 1.083 1.356 1.782 2.681 3.055
13 | 0.259 0.538 0.694 0.870 1.079 1.350 1.771 2.650 3.012
14 | 0.258 0.537 0.692 0.868 1.076 1.345 1.761 2.624 2.977
15 | 0.258 0.536 0.691 0.866 1.074 1.341 1.753 2.602 2.947
16 | 0.258 0.535 0.690 0.865 1.071 1.337 1.746 2.583 2.921
17 | 0.257 0.534 0.689 0.863 1.069 1.333 1.740 2.567 2.898
18 | 0.257 0.534 0.688 0.862 1.067 1.330 1.734 2.552 2.878
19 | 0.257 0.533 0.688 0.861 1.066 1.328 1.729 2.539 2.861
20 | 0.257 0.533 0.687 0.860 1.064 1.325 1.725 2.528 2.845
21 | 0.257 0.532 0.686 0.859 1.063 1.323 1.721 2.518 2.831
22 | 0.256 0.532 0.686 0.858 1.061 1.321 1.717 2.508 2.819
23 | 0.256 0.532 0.685 0.858 1.060 1.319 1.714 2.500 2.807
24 | 0.256 0.531 0.685 0.857 1.059 1.318 1.711 2.492 2.797
25 | 0.256 0.531 0.684 0.856 1.058 1.316 1.708 2.485 2.787
26 | 0.256 0.531 0.684 0.856 1.058 1.315 1.706 2.479 2.779
27 | 0.256 0.531 0.684 0.855 1.057 1.314 1.703 2.473 2.771
28 | 0.256 0.530 0.683 0.855 1.056 1.313 1.701 2.467 2.763
29 | 0.256 0.530 0.683 0.854 1.055 1.311 1.699 2.462 2.756
30 | 0.256 0.530 0.683 0.854 1.055 1.310 1.697 2.457 2.750
31 | 0.256 0.530 0.682 0.853 1.054 1.309 1.696 2.453 2.744
32 | 0.255 0.530 0.682 0.853 1.054 1.309 1.694 2.449 2.738
33 | 0.255 0.530 0.682 0.853 1.053 1.308 1.692 2.445 2.733
34 | 0.255 0.529 0.682 0.852 1.052 1.307 1.691 2.441 2.728
35 | 0.255 0.529 0.682 0.852 1.052 1.306 1.690 2.438 2.724
36 | 0.255 0.529 0.681 0.852 1.052 1.306 1.688 2.434 2.719
37 | 0.255 0.529 0.681 0.851 1.051 1.305 1.687 2.431 2.715
38 | 0.255 0.529 0.681 0.851 1.051 1.304 1.686 2.429 2.712
39 | 0.255 0.529 0.681 0.851 1.050 1.304 1.685 2.426 2.708
40 | 0.255 0.529 0.681 0.851 1.050 1.303 1.684 2.423 2.704
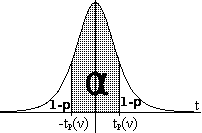 podemos tomar como
valor aproximado el de la última fila, que se aproxima al de la
distribución normal, correspondiente a ν=∞. Si queremos obtener un
intervalo de confianza de α
centrado en el valor promedio esperado (ver figura) deberemos tomar
p=(α+1)/2. Obtenidos los valores de
podemos tomar como
valor aproximado el de la última fila, que se aproxima al de la
distribución normal, correspondiente a ν=∞. Si queremos obtener un
intervalo de confianza de α
centrado en el valor promedio esperado (ver figura) deberemos tomar
p=(α+1)/2. Obtenidos los valores de 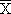 ,
σ(
,
σ(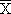 ), ν y p, y extrayendo de la tabla el
coeficiente crítico tp(ν), el intervalo de
confianza vendrá dado por
), ν y p, y extrayendo de la tabla el
coeficiente crítico tp(ν), el intervalo de
confianza vendrá dado por 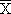 -tp(ν)·σ(
-tp(ν)·σ(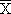 )
,
)
, 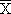 +tp(ν)·σ(
+tp(ν)·σ(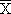 )
].
)
].
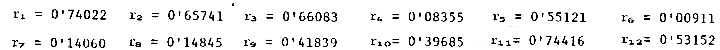

| mes | lote entregado | inventario inicial mes | probabilidad para demanda | demanda estimada | factor estacional | demanda corregida | inventario fin mes | ruptura | nº orden pedido | probabilidad para tiempo pedido | tiempo de entrega | inventario mensual promedio |
| 1 | 0 |
150 | 0'74022 | 1'2 | ||||||||
| 2 | 0'65741 | 1'0 | ||||||||||
| 3 | 0'66083 | 0'9 | ||||||||||
| 4 | 0'08355 | 0'8 | ||||||||||
| 5 | 0'55121 | 0'8 | ||||||||||
| 6 | 0'00911 | 0'7 | ||||||||||
| 7 | 0'14060 | 0'8 | ||||||||||
| 8 | 0'14845 | 0'9 | ||||||||||
| 9 | 0'41839 | 1'0 | ||||||||||
| 10 | 0'39685 | 1'2 | ||||||||||
| 11 | 0'74416 | 1'3 | ||||||||||
| 12 | 0'53152 | 1'4 |
| moderadamente el
consumo
energético y (3) reducir
drásticamente el consumo energético, en relación a
los siguientes escenarios: (a) fuentes de energía actualmente
existentes, (b) descubrimiento de una fuente de energía
radicalmente nueva y (c) posibilidad de trasladarse a otro planeta
virgen con abundancia de recursos, suponiendo que las probabilidades de
los escenarios son P(a)=0'6, P(b)=0'3, P(c)=0'1 y que las
probabilidades
condicionales de conseguir el objetivo de que la humanidad viva
satisfactoriamente
vienen dadas por la tabla adjunta. |
|
|||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||