Llicenciatura en Ciències Químiques
GUIA DIDÀCTICA
Rafael Pla López
Departament de Matemàtica Aplicada
Universitat de València
curs 2009-2010
Objectius:
Específics:
- Determinar
l'error del resultat d'un càlcul a
partir
de l'error de les dades de les quals partim (PROPAGACIÓ
D'ERRORS).
- Inferir informació sobre poblacions a partir d'una porció de les mateixes (INTRODUCCIÓ A L'ESTADÍSTICA).
- Aprendre a obtenir mides de centralització i dispersió en una distribució estadística.
- Estudiar casos
típics de distribucions
estadístiques de probabilitats.
- Fer estimacions sobre una població a partir d'una mostra.
- Obtenir una recta que tinga la menor desviació possible d'un conjunt de punts.
- Estimar si un conjunt de
mostres pertanyen a la
mateixa
població.
- Obtenir aproximacions discretes a la solució de diferents problemes (INTRODUCCIÓ AL CÀLCUL NUMÈRIC).
- Interpolar el valor d'una funció polinòmica desconeguda que passe per un conjunt de punts.
- Aproximar la integració d'una funció, acotant l'error d'aproximació.
- Obtenir el valor futur d'una variable coneixent el seu valor inicial y la dependència de la seua derivada respecte del temps i la mateixa variable, y'=f(t,y).
- Aprendre a utilitzar un llenguatge de programació o un paquet informàtic, a elecció del professorat de cada grup de pràctiques.
- Aprendre a treballar en equip.
- Aprendre a exposar públicament un treball.
- Adquirir respecte pels companys que exposen un treball, atenent-los i ajudant-los en cas necessari.
- Aprendre a realitzar raonaments deductius per a demostrar un enunciat a partir de determinades premisses.
- Adquirir la capacitat de qüestionar la fiabilitat dels resultats obtinguts per mètodes numèrics i estadístics.
- Treball en classe en grups menuts debatent textos, demostrant enunciats i resolent problemes, seguit de la seua exposició pública.
- Treball en equip fora de classe, elaborant treballs per a la seua presentació al professor.
- Treball pràctic en aula d'informàtica.
- La qualificació final serà la mitjana de la nota de teoria i la nota de pràctiques, sempre que ambdues siguen igual o superior a 4 (sobre un màxim de 10).
- Per a la nota de teoria puntuarà fins a 8 punts l'avaluació d'un examen final individual escrit, i fins a 2 punts la realització de treballs en equip, que solament podran considerar-se en cas d'assistència regular a classe (en cas contrari, haurien de respondre's qüestions addicionals en l'examen final puntuables fins als 2 punts restants). Es podrà consultar aquesta Guia Didàctica i un formulari escrit a mà personalment en un màxim de 3 fulls sense problemes resolts (no s'admeten fotocòpies). A més, es prevaldrà la participació activa en classe sumant una dècima per cada exposició pública d'un treball realitzat en classe.
- La nota de pràctiques es determinarà
per
l'avaluació de les memòries presentades de les
pràctiques realitzades i de l'avaluació d'un
examen
pràctic individual en ordinador, el qual puntuarà
entre
el 40 i el
60% de la nota de pràctiques (percentatge a determinar pel
professorat de cada grup de pràctiques).
Bibliografia:
Estadística:
- Canavos, G.C. (1987), Probabilidad y Estadística. Aplicaciones y Métodos, McGrawHill
- Christensen, M.B. (1983), Estadística paso a paso, Trilla, Mexico
- Cuadras, C.M. (1986), Problemas de Probabilidad y Estadística, Anaya, Madrid
- Dwnie, N.M., Heath, R.W. (1971), Métodos de Estadística Aplicada, Ed.del Castillo, Madrid
- Dowdy, S., Wearden, S. (1991), Statistics for Research, Wiley & sons
- Fz.de Troconiz, A. (1987), Probabilidades, Estadística, Muestreo, Ed.Tébar Flores, Madrid
- Gmurman, V.E. (1974), Teoría y Problemas. Estadística Matemática, Mir, Moscu
- Gutiérrez, S. (1976), Estadística Aplicada, ed.facsímil, València
- Gutiérrez Cabria, S., Probabilidades, Bioestadística, Ed.Tebar Flores, Madrid
- Haber, A., Runyon, R.P. (1973), Estadística General, Fondo Educativo Iberoamericano
- Labrousse, C. (1968), Estadística, Colección Univ.de Matemática Pura, Madrid
- Martínez Salas, HJ. (1989), Métodos Matemáticos, Ed.el autor, Valladolid
- Mendenhall, W., Scheaffer, R.L., Wackely, D.D. (1986), Estadística Matemática con Aplicaciones, Grupo Editorial Iberoamérica
- Milton, T. (1987), Estadística para Biología y Ciencias de la Salud, InteramericanaMcGrawHill
- Ortle, B. (1970), Estadística Aplicada, LinusaWiley, Mexico
- Quesada, V., Isidoro, A., Löpez, L.A. (1984), Curso y Ejercicios de Estadística, Alhambra Universidad
- Sachs, I. (1978), Estadística Aplicada, Labor, Barcelona
- Spiegel, M.R. (1979), Estadística, Schaum/McGrawHill, México
- Spiegel, M.R. (1976), Probabilidad y estadística, Schaum/McGrawHill, México
- Williams, B. (1993), Biostatistic, Chapman & Hall
Càlcul Numèric:
- Aubanell, A., Benseny, A., Delshams, A. (1991), Eines bàsiques de Càlcul Numèric, Universitat Autònoma de Barcelona, Bellaterra
- Aubanell, A., Benseny, A., Delshams, A. (1993), Útiles básicos de Cálculo Numérico, Editorial Labor, Barcelona
- Chapra, S.C., Canale, R.P. (1985), Métodos numéricos para ingenieros (con aplicaciones en computadoras personales), McGrawHill, Mexico
- Conte, S.D., Boor, C.de (1974), Análisis numérico elemental, McGrawHill, México
- Cordero, A., Hueso, J.L, Martínez, E., Torregrosa, J.M. (2006), Problemas Resueltos de Métodos Numéricos, Thomson, España
- Denidovich, B.P., Maron, I.A. (1988), Cálculo Numérico Fundamental, Paraninfo, Madrid
- Douglas, J., Burden, R. (2004), Métodos Numéricos, Thomson, España
- Martínez Salas, J. (1989), Métodos Matemáticos, Ed.el autor, Valladolid
- Ralston, A. (1985), Introducción al Análisis Numérico, Linusa, Mexico
- Scheid, F. (1990), Análisis Numérico, McGrawHill, Mexico
- Scheid, F. Constanzo, R.E.di (1991), Métodos Numéricos, McGrawHill
0. Determinar l'error del resultat d'un càlcul a partir de l'error de les dades de les quals partim (PROPAGACIÓ D'ERRORS):
Activitat 0.1. Les dades experimentals amb les que treballem venen sempre donades amb un cert error. Si a partir d'elles realitzem càlculs, aquests errors es propaguen als resultats. Així, si y=f(x), tindrem que ∆y=f(x+∆x)-f(x). Tanmateix, si l'ordre de magnitud de l'error és prou inferior a l'ordre de magnitud de les dades, podem estimar l'error per la diferencial, prenent així ∆y≈f ' (x)·∆x .
Problema 0.1: si y=x2, estimar l'error de y en els següent casos:
a) x=2±1.
b) x=2'0±0'1
c) x=2'00±0'01
En quins casos la diferencial donarà una bona estimació de l'error (expressant aquest amb una única xifra significativa, o 2 si la primera és 1)?.
Activitat 0.2.
Exercici 0.1: tenint en compte que si z=f(x,y) aleshores dz = fx'·∆x + fy'·∆y , obtenir l'expressió aproximada de l'error de z si z=x+y, z=x·y, z=x/y, z=x2, z=√x .
Activitat 0.3.
Problema 0.2: suposem que una reacció ve regida per la llei d'acció de mases v=k·[A]·[B]2, amb k=0'254±0'001. Si es mesuren les concentracions en equilibri obtenint-se [A]=7'23±0'04 mols/l, [B]=9'58±0'12 mols/l, estimar l'error de la velocitat de reacció en equilibri.
1. Inferir informació sobre poblacions a partir d'una porció de les mateixes (INTRODUCCIÓ A L'ESTADÍSTICA):
Activitat 1.1:
Debatir en
grups menuts el següent text, escollint prèviament un
portaveu
de cada grup per exposar posteriorment les conclusions i en el seu cas
les dubtes suscitades:
En nombrosos problemes
pràctics estem interessats en propietats globals de poblacions,
més que en les
propietats particulars de cadascun dels individus que les composen.
Aquestes propietats globals de les poblacions (i entenem per
població qualsevol conjunt, els elements del qual
són
tractats de forma indiferenciada) són l'objecte de
l'Estadística:
des d'un punt de vista estadístic, allò que
interessa no
és quins individus tenen una propietat determinada,
sinó
quants la tenen.
Ara bé,
normalment no tenim accés a les poblacions en el seu
conjunt,
sinó solament a porcions de les mateixes (a les quals
anomenem mostres),
i ens interessa poder
inferir propietats globals a partir de l'estudi d'aquestes porcions.
Aquesta inferència és l'objectiu
central de l'Estadística.
La
inferència
estadística és fonamental per a la
investigació
científica: habitualment, es construeixen teories globals
sobre
poblacions, les quals es contrasten amb estudis experimentals sobre
mostres de les mateixes. Però és important
recalcar que
la inferència estadística solament permet arribar
a
estimacions, i no a afirmacions concloents.
Per tot
això,
podríem dir que l'Estadística, per la seua pròpia
natura,
és una ciència "democràtica"
pel seu objecte (poblacions globals, que poden ser tant d'objectes
inanimats com de persones humanes) i "antidogmàtica"
pel seu mètode, el qual exclou certeses definitives.
1.1. Aprendre a obtenir mides de centralització i dispersió en una distribució estadística:
Objectius:
- Comprendre la noció de distribució estadística i la seua no dependència de les propietats específics d'individus específics.
- Aprendre a comparar diferents distribucions estadístiques pel valor al voltant del qual s'agrupen els seus valors.
- Aprendre a comparar diferents distribucions estadístiques per la dispersió dels seus valors.
- Entendre en quina mesura varien les mesures de centralització i dispersió d'una distribució estadística al sumar, restar, multiplicar o dividir els seus valors per una quantitat fixa.
- Aprendre a calcular les mesures de centralització i dispersió de manera que se simplifiquen els càlculs i s'eviten els errors de cancel·lació.
- Aprendre a normalitzar les distribucions
estadístiques per
tal de fer-les comparables més enllà de les seues
mesures
de centralització i dispersió.
Activitat 1.2. Una variable
aleatòria (X) sobre un
conjunt-població U és qualsevol variable que pot
tenir
distints valors (x) per als distints elements-individus de la
població. La distribución
estadística d'aquests valores no té
en compte els
individus concrets per als que aquesta variable té cada
valor,
sino quants la tenen, al que anomenem freqüència
f(x) d'aquest valor en la població. Anomenarem paràmetre
poblacional a qualsevol quantitat que solament depenga de
les
freqüències. Dues variables aleatòries seran
estadísticament equivalents
quan tinguen la mateixa distribució de
freqüències.
Exercici 1.1:
prendre
una variable aleatòria sobre l'alumnat assistent a la
classe,
per exemple el fet de portar o no portar ulleres, i realitzar un
experiment senzill per tal de comprovar que el número dels
que
porten ulleres és un paràmetre poblacional.
Activitat 1.3.
Exercici 1.2:
representar gràficament en diagrames de barres la
distribució
estadística de les freqüències
del
número de calcer i de l'edat en l'alumnat assistent a
classe.
Activitat 1.4.
Com a mesures de
centralitat
(valor
al voltant del qual s'agrupen els valors de la variable
aleatòria) podem prendre:
La moda:
aquell valor que
tinga la màxima freqüència en la
població.
La mediana:
suposant que el
conjunt de valors de la variable aleatòria esté
ordenat,
serà un valor que tinga tants individus amb un valor
inferior
com amb un valor superior.
La mitjana
μ(X): suposant que
els
valors de la variable aleatòria siguen números
reals, i
que la grandària
(número d'individus n(U)) de la població siga
finit, ve
donada per la
suma dels valors Xi
per a tots els individus
i de la població
dividida
per la seua grandària, μ(X) = ∑ i
Xi
/ n(U) .
Teorema 1.1:
∑
x f(x) = n(U)
, μ(X) = ∑
x x·f(x) / n(U) .
Problema 1.1:
calcular
les diferents mesures de centralització per a les
distribucions
estadístiques de l'Activitat 1.3. Com podem utilitzar les
freqüències per simplificar els càlculs?
Activitat 1.5.
Per
justificar que el càlcul de la mitjana és una
operació lineal, demostrar els següents teoremes:
Teorema 1.2:
si tenim
dues variables aleatòries X, Y amb valors
numèrics reals
sobre la mateixa població U,
μ(X+Y)=μ(X)+μ(Y) .
Teorema 1.3:
si tenim
una variable aleatòria sumable X y un número real
constant c, μ(c·X)=c·μ(X) .
Activitat 1.6.
A partir de
la linealitat del càlcul de la mitjana expressada als dos
teoremes anteriors, i tenint en compte que la mitjana d'una constant
és igual a la mateixa constant, demostrar
Teorema 1.4:
si tenim
una variable aleatòria X amb valors numèrics
reals i un
número real acR,
aleshores μ(X)=a+μ(X-a) .
Teorema 1.5:
si tenim
una variable aleatòria X amb valors numèrics
reals i dos
números reals a,ccR,
i prenem Y=(X-a)/c, aleshores μ(X)=a+c·μ(Y) .
Els teoremes anteriors es poden utilitzar per a simplificar el
càlcul de la mitjana. Aplicar-ho per a la
resolució del
Problema 1.2:
midar la
longitud de la pròpia mà amb una
precisió de 0'5
cm i calcular la mitjana del conjunt de l'alumnat assistent a classe.
Activitat 1.7.
Com a mesures
de dispersió
(per expressar l'allunyament entre sí dels valors d'una
variable
aleatòria) podem prendre:
Els quartils
primer i
tercer: suposant que el conjunt de valors de la variable
aleatòria
esté ordenat, els quartils seran tres valors que
dividisquen al conjunto de valors en quatre subconjunts de valors que
corresponguen al mateix número d'individus; observem que
el segon quartil coincidirà amb la mediana. Si tenim
definida una distància en el conjunt de valors, podem
mesurar la
dispersió com la distància entre el primer i el
tercer
quartil.
La amplitut:
suposant que els
valors estiguen ordenats i tinguem definida una distància
entre
ells, serà la distància entre els valors
mínim i
màxim en la població.
La desviació
mitjana:
suposant que els valors de la variable aleatòria siguen
números reals i que la grandària de la
població
siga finita,
serà la mitjana del valor absolut de las
diferèncias
entre el seu
valor per a cada individu i la mitjana d'aquests valors,
μ(|X-μ(X)|)
La variància
σ2(X):
suposant que els valors de la variable aleatòria siguen
números reals i que la
grandària de la població siga finita,
serà la
mitjana
del quadrat de les diferències entre el seu valor per a cada
individu i la mitjana d'aquests valors, σ2(X)=μ((X-μ(X))2).
La desviació
típica
σ(X): és l'arrel quadrada de la variància.
Demostrar el
Teorema 1.6:
σ2(X)=μ(X2)-μ(X)2
(la variància és igual a la mitjana
dels quadrats menys el quadrat de la mitjana).
Aquest teorema proporciona una forma més còmoda
de
calcular la variància.
Problema 1.3:
calcular
les diferents mesures de dispersió per a les distribucions
estadístiques de l'Activitat 1.3.
Problema 1.4:
calcular
la variància d'aquest conjunt de valors: (1000000'1,
1000000'2,
1000000'2, 1000000'3).
Activitat 1.8.
Com haurem
vist a l'intentar resoldre el Problema 1.4, si la mitjana d'una
distribució estadística és molt
més gran
que la seua amplitud,
aleshores la mitjana del quadrat i el quadrat de la mitjana tindran
moltes xifres significatives coincidents, que poden fins i
tot
superar la precisió dels nostres instruments de
càlcul;
en aquest cas, obtindríem erròniament zero com la seua
diferència, produint-se així un "error de
cancel·lació". Per tal de poder evitar-ho utilitzant les
propietats de la variància, demostrar el
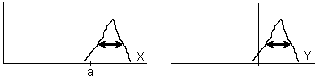 Teorema 1.7:
si tenim
una variable aleatòria X amb valors numèrics
reals i un
número real acR,
i prenem Y=X-a, aleshores σ2(Y)=σ2(X)
, és a dir, la variància és invariant
davant
translacions, com es pot entendre fàcilment observant la
figura
adjunta.
Teorema 1.7:
si tenim
una variable aleatòria X amb valors numèrics
reals i un
número real acR,
i prenem Y=X-a, aleshores σ2(Y)=σ2(X)
, és a dir, la variància és invariant
davant
translacions, com es pot entendre fàcilment observant la
figura
adjunta.
Per tant, podrem evitar l'error de cancel·lació restant a
tots
els
valors una quantitat fixa
pròxima al
seu valor mínim. Aplicar-ho a la resolució del
Problema
1.4.
Activitat 1.9.
Demostrar el
Teorema 1.8:
si tenim
una variable aleatòria X amb valors numèrics
reals i dos
números reals a,ccR+,
i prenem Y=(X-a)/c, aleshores
σ(X)=c·σ(Y) .
Aplicar-ho per simplificar la resolució del
Problema 1.5:
calcular
la variància de la distribució
estadística del
Problema 1.2.
Activitat 1.10.
Per comparar
la forma de distribucions estadístiques amb diferents
mitjanes i
variances podem transformar-les en altres distribucions
estadístiques amb mitjanes i variances coincidents.
Anomenarem
així normalització
de una variable aleatòria X al resultat de restar-li la seua
mitjana i dividir la
diferència per la seua desviació
típica,
N(X)=(X-μ(X))/σ(X) . Demostrar el
Teorema 1.9:
μ(N(X))=0 i σ(N(X))=1.
Exercici 1.3:
Representar gràficament en la mateixa figura la
normalització de les distribucions estadístiques
de
l'Activitat 1.3.
1.2. Estudiar casos típics de distribucions estadístiques de probabilitats:
Objectius:
- Treballar les distribucions estadístiques a partir de les freqüències relatives (probabilitats).
- Averiguar la distribució probabilística del número d'ocurrències d'un succés entre un número d'ocasions independents. (distribució binomial).
- Aproximar la distribució probabilística del número d'ocurrències d'un succés rar coneixent el número mitjà d'ocurrències entre un número gran d'ocasions independents (distribució de Poisson).
- Introduir la distribució de densitat probabilística d'una variable aleatòria que varia de forma contínua.
- Estudiar la distribució de densitat probabilística de la mitjana d'un gran número de variables aleatòries equivalents independents (distribución normal).
Demostrar els següents teoremes:
Teorema 1.10: ∑ x p(x) = 1 (anomenarem distribució probabilística a qualsevol aplicació p:V→R++{0} que acomplisca aquesta propietat, essent V un conjunt numerable de valors).
Teorema 1.11: μ(X) = ∑ x x·p(x) (utilitzarem aquesta expressió per definir la mitjana de qualsevol distribució probabilísitica amb independència de la grandària finita o infinita de la població).
Exercici 1.4: representar gràficament en diagrames de pastís les distribucions probabilístiques de les variables aleatòries de l'activitat 1.3.
Activitat 1.12. Si tenim un conjunt A de valors d'una variable aleatòria, la seua probabilitat vindrà definida per
p(A) = ∑ xcA p(x) . Demostrar el
Teorema 1.12: Si A i B són dos conjunts disjunts de valors d'una variable aleatòria, p(A+B) = p(A) + p(B) .
Activitat 1.13. Direm que dues variables X, Y són independents si per a qualsevol parell (x, y) de valors respectius de les mateixes s'acompleix p(x,y)=p(x)·p(y) .
Problema 1.6: estudiar si les variables aleatòries de l'Activitat 1.3 són independents.
Activitat 1.14. Tenint en compte el
Teorema -1.1: el número de maneres en que podem escollir m elements entre n és
| ﴾ |
n m |
﴿ = |
n(n-1)(n-2)...(n-(m-1))
m! |
= |
n!
m!(n-m)! |
(combinacions
de n sobre m) |
Teorema 1.13: Si tenim n variables-ocasions independents amb un determinat valor-succés amb la mateixa probabilitat p, la probabilitat de no ocurrència de cada succés serà q=1-p i la probabilitat de que el número d'ocurrències del succés siga exactament m serà
| PB(m)
= ﴾ |
n m |
﴿ pm
qn-m (distribució
binomial B(p,n)) |
Problema 1.7: calcular la probabilitat d'obtenir exactament 3 asos en 5 llançaments d'un dau.
Activitat 1.15. Tenint en compte el
| Teorema -1.2:
(a+b)n
= |
n ∑ m=0 |
﴾ | n m |
﴿ am
bn-m (binomi
de Newton) |
| Teorema 1.14:
|
n ∑ m=0 |
PB(m) = 1 |
Activitat 1.16. Tenint en compte el
Teorema -1.3: 0!=1 , m!=m·(m-1)!
demostrar els
| Teorema 1.15:
per a tot
m=1...n, ﴾ |
n m |
﴿·m = n·﴾ | n-1 m-1 |
﴿ |
Activitat 1.17. Demostrar els
| Teorema 1.17:
per a tot
m=2...n, m·﴾ |
n-1 m-1 |
﴿ = (n-1)·﴾ | n-2 m-2 |
﴿ + ﴾ | n-1 m-1 |
﴿ |
Activitat 1.18.
Problema 1.8: obtenir la mitjana i la desviació típica del número d'asos al llançar 30 vegades un dau.
Activitat 1.19. Si p és molt xicotet, per a obtenir una mitjana μ apreciable d'ocurrències d'un succés necessitarem un número n molt gran d'ocasions. Però els factorials n!, i per tant la distribució binomial, són difícils de calcular si n és gran. En aquest cas, haurem d'utilitzar una aproximació. A tal efecte, i tenint en compte que e = lim u→∞ (1+1/u)u, i per tant
Teorema -1.4: lim n→∞ (1-μ/n)n = e-μ
demostrar el
Teorema 1.19: si p=μ/n, PΠ(m) = lim n→∞ PB(m) = e-μ·μm/m! (distribució de Poisson Π(μ)).
La distribució de Poisson és una bona aproximació a la binomial si n>50, p<0'1 i μ=np<5 .
Activitat 1.20. Tenint en compte el
| Teorema -1.5: eμ = | ∞ ∑ m=0 |
μm/m! (desenvolupament en sèrie de Taylor de l'exponencial) |
| Teorema 1.20: | ∞ ∑ m=0 |
PΠ(m) = 1 |
Teorema 1.22: σ(Π(μ))2 = μ
Activitat 1.21.
Problema 1.9: suposant que la probabilitat d'obtenir un preparat químic per un determinat procediment siga de 0'01, quin serà el número mitjà d'èxits i la probabilitat de tenir al menys un èxit en 200 proves? Obtenir el valor exacte per la distribució binomial i el valor aproximat per la distribució de Poisson i comparar-los.
Activitat 1.22. Si tenim una variable aleatòria que varia de forma contínua en R, haurem de definir un conjunt d'intervals de la mateixa per determinar les freqüències o probabilitats dels valors en cada interval,
 com
vam fer al Problema 1.2 amb la longitud de la mà.
Però
podem definir també una distribució
de densitat probabilística
mitjançant una
funció p:R→R++{0} que
acomplisca ∫ p(x) dx = 1
.
com
vam fer al Problema 1.2 amb la longitud de la mà.
Però
podem definir també una distribució
de densitat probabilística
mitjançant una
funció p:R→R++{0} que
acomplisca ∫ p(x) dx = 1
. En aquest cas, la probabilitat d'un interval [a,b[ vindrà donada per
p([a,b]) = ∫ab p(x) dx
Naturalment, si fem una partició de R en un conjunt d'intervals disjunts, la suma de les seues probabilitats valdrà 1. A partir del
Teorema -1.6: per a tota funció integrable f i tot interval [a,b[ de R, existeix ξc[a,b[ tal que
∫ab x·p(x) dx = ξ·∫ab p(x) dx
demostrar el
Teorema 1.23: si tenim una distribució p de densitat probabilísitca, partim R en intervals disjunts [z-ε,z+ε[ prenent z com valor de l'interval, i definim la mitjana de la distribució de densitat probabilística com el límit de la mitjana de la corresponent distribució probabilística quan ε tendisca a zero, serà
μ(X) = ∫ x·p(x) dx .
Teorema 1.24: definint la variància d'una distribució p de densitat probabilística com μ((X-μ(X))2), serà
σ2(X) = ∫ x2·p(x) dx - μ(X)2 .
Activitat 1.23. Definim la distribució normal N(α,β) per PN(x) = e-(x-α)2/(2β2)/(β(2π)1/2) per a tot xcR .
Tenint en compte el
Teorema -1.7: ∫-∞∞ e-u2du = √π , ∫-∞∞ ue-u2du = 0 , ∫-∞∞ u2e-u2du = (√π)/2
demostrar els
Teorema 1.25: ∫-∞∞ PN(x) dx = 1 (i per tant es tracta d'una distribució de densitat probabilística)
Teorema 1.26: μ(N(α,β)) = α
Teorema 1.27: σ(N(α,β)) = β
Escriurem per tant N(μ,σ) i PN(x) = e-(x-μ)2/(2σ2)/(σ(2π)1/2) .
Activitat 1.24. Definim la distribució normal tipificada com N(0,1), de manera que PN(y) = e-y2/2/(2π)1/2 .
Treballarem amb la tabla de la distribución normal tipificada. A partir d'aquesta, podem obtenir fàcilment els valors d'altra distribució normal mitjançant la normalització de la seua variable x, de manera que y=(x-μ)/σ , i tenint en compte que PN(y)=σ·PN(x) .
Problema 1.10. Utilitzant la tabla de la distribució normal tipificada, obtenir la densitat probabilística d'una distribució normal amb μ=5, σ=2 per a x=7'4.
Activitat 1.25. La importància de la distribució normal per a l'estudi de l'Estadística resulta justificada pel següent
Teorema 1.28: si tenim una successió de variables aleatòries independents Xi amb la mateixa mitjana i desviació típica, μ(Xi)=μ, σ(Xi)=σ, i definim Zn = ∑i=1 n Xi/n , aleshores la distribució estadística de lim n→∞ N(Zn) és la distribució normal tipificada N(0,1) (Teorema central del límite).
D'acord amb aquest teorema, la distribució normal donarà una bona aproximació de la mitjana d'un gran número de variables aleatòries equivalents independents, i podrem utilitzar-la quan treballem amb grans quantitats de dades. En particular, s'acompleix el
Teorema 1.29: lim n→∞ PB(p,n)(m) / PN(np,√(np(1-p)))(m) = 1 (teorema de De Moivre; per a cada valor de m, la successió de valors de n serà n=m, m+1, m+2...)
La distribució normal és una bona aproximació a la binomial si n·p>5 i n·q>5 .
Problema 1.11: comparar les distribucions normal, binomial i de Poisson en els següents casos:
a) Aplicar la distribució normal per intentar aproximar la solució del Problema 1.9. Dóna una bona aproximació?
b) Suposant que la probabilitat d'obtenir un preparat químic per un determinat procediment siga de 0'5, quina serà la probabilitat de tenir únicament un fracàs en 10 proves? Obtenir el valor exacte per la distribució binomial i intentar aproximar-ho per les distribucions normal i de Poisson. Quina dóna una millor aproximació?
Treball 1 (per a la seua realització en equip):
Estudiar les condicions d'aproximació de les distribucions normal y de Poisson a la distribució binomial, utilitzant diferents fonts bibiogràfiques (per exemple
http://www.gestiopolis.com/recursos/experto/catsexp/pagans/eco/44/distripoisson.htm
http://www.suagm.edu/paginas/japaricio/384/clase11.pdf
http://www.jstor.org/sici?sici=0003-4851(196009)31%3A3%3C737%3ATPATTP%3E2.0.CO%3B2-Q&cookieSet=1
http://leonsotelo.blogspot.com/2007/06/aproximacion-normal-binomial-poiss0n.html
http://www.mitecnologico.com/Main/AproximacionDeBinomialPorDePoisson )
Estudiar i comparar en particular el cas n=30, p=1/6. Obtenir una tabla de les tres distribuciones (per a valors enters no negatius) i representar-les gràficament en la mateixa figura.
1.3. Fer
estimacions sobre una població a partir d'una mostra:
Objectius:
- Estudiar les propietats de les distribucions de les mostres d'una població.
- Identificar els estadístics-paràmetres d'una mostra que millor permeten estimar els paràmetres de la població.
- Construir intervals que continguen amb una certa probabilitat el valor d'un paràmetre poblacional.
- Determinar la probabilitat d'equivocar-nos al rebutjar una hipòtesi a partir d'unes dades experimentals.
- Treballar amb les distribucions adequades segons les mostres utilitzades i els paràmetres a estimar.
- Contrastar hipòtesis probabilístiques.
Activitat 1.26.
Una mostra sense
reemplaçament
és qualsevol subconjunt d'una població (un
exemple
típic és una mà de cartes d'una
baralla). Una mostra
amb reemplaçament
s'obté escollint successivament un determinat
número
d'elements de la població sense llevar-los de la mateixa, de
manera que poden repetir-se (un exemple típic és
el
resultat de tirades successives d'un dau). Anomenarem estadístic
a qualsevol
paràmetre poblacional restringit a una mostra. Per a
distingir-lo del corresponent paràmetre sobre la
població, utilitzarem una nomenclatura diferent;
així,
designarem la mitjana d'una variable aleatòria X en una
mostra
per  , i
la seua desviació típica per s(X).
, i
la seua desviació típica per s(X).
Treballarem amb distribucions en 3 àmbits: en la
població, en una mostra i en el conjunt de totes les
mostres.
Naturalment, per poder fer estimacions sobre una població a
partir d'una mostra necessitarem saber com es distribueixen els valors
de l'estadístic corresponent en el conjunt de totes les
mostres
de la població d'un determinat tipus (amb o sense
reemplaçament) i d'una determinada grandària; a
aquesta
distribució l'anomenarem distribució
mostral. Les principals propietats d'aquesta es resumeixen
en la
següent tabla, on indiquem per n(U) la grandària de
la
població i per n la grandària de la mostra:
| paràmetre poblacional Ω |
estadístic S |
distribució mostral sense
reemplaçament μ(S), σ(S) |
distribució mostral amb
reemplaçament μ(S), σ(S) |
| μ(X) |
 |
μ( )
= μ(X) )
= μ(X) |
|
σ( )2
= σ(X)2(n(U)-n)/(n·(n(U)-1)) )2
= σ(X)2(n(U)-n)/(n·(n(U)-1)) |
σ( )2
= σ(X)2/n )2
= σ(X)2/n |
||
| σ(X) |
s(X) |
μ(s(X)2)
= σ(X)2·(n-1)/n σ(s(X))2 ≈ σ(X)2/(2n) si n≥100 |
|
Problema 1.12: Obtenir la variància de la distribució mostral de mitjanes i la mitjana de la distribució mostral de variances amb mostres formades per la repetició 3 vegades del llançament de 5 daus anotant en cada llançament el número d'asos obtinguts (suposant que els daus no estan carregats). Dividir la classe en grups de 3 de manera que cada membre faça un llançament de 5 daus, calculant en cada grup la mitjana i la variància de la mostra obtinguda. Calcular la variància de les mitjanes i la mitjana de les variances obtingudes per tota la classe i comparar-les amb els previs resultats teòrics.
Activitat 1.27.
Per a
estimar correctament un paràmetre poblacional Ω
necessitarem un
estadístic S que siga un estimador
inesbiaixat del mateix, de manera que μ(S) =
Ω. En cas que no ho siga però coneguem
l'esbiaixada que es
produeix, de manera que μ(S) = f(Ω), essent f una
funció lineal,
podem definir un estimador corregit 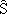 = f -1(S)
tal que μ(
= f -1(S)
tal que μ(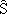 )
= Ω .
)
= Ω .
Exercici 1.5:
analitzar si la mitjana  i la variància s2
són o no estimadors inesbiaixats dels corresponents
paràmetres poblacionals μ(X) i σ(X). En cas
que algú no
ho siga, obtenir el corresponent estadístic corregit i
comprovar
que és un estimador inesbiaixat.
i la variància s2
són o no estimadors inesbiaixats dels corresponents
paràmetres poblacionals μ(X) i σ(X). En cas
que algú no
ho siga, obtenir el corresponent estadístic corregit i
comprovar
que és un estimador inesbiaixat.
 Activitat 1.28. Si tenim dos
estimadors
inesbiaixats S1 i S2,
direm que S1
és més eficient
que S2 si i solament
si σ(S1)<σ(S2).
Activitat 1.28. Si tenim dos
estimadors
inesbiaixats S1 i S2,
direm que S1
és més eficient
que S2 si i solament
si σ(S1)<σ(S2).
Exercici 1.6:
volem
estimar la mitjana μ d'una població a partir de les
mitjanes
 1,
1,
 2
de dues mostres de grandària respectiva n1,
n2 tals que n1<n2.
Quin estimador serà més eficient? Demostrar-ho.
2
de dues mostres de grandària respectiva n1,
n2 tals que n1<n2.
Quin estimador serà més eficient? Demostrar-ho.
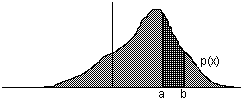
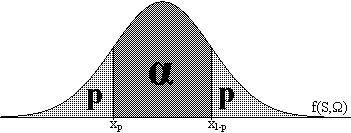 Activitat
1.29. Direm que [Ω1,Ω2]
és un interval de
confiança
del 100α% per a un paràmetre poblacional
Ω si la probabilitat de
que Ω estiga dins d'aquest interval és igual a
α. Per
determinar-ho necessitarem conèixer la
distribució
mostral d'alguna funció f(S,Ω), essent S
l'estadístic
d'una mostra que utilitzem per estimar Ω. En general,
buscarem en
aquesta distribució mostral de densitat
probabilística
dos "pics" de probabilitat p, de manera que l'àrea entre els
dos
"pics" siga α, tal com s'indica en la figura adjunta.
Observem que, per
tal com l'àrea baix de la corba és 1, s'ha
d'acomplir 2p+α=1.
Les abcises corresponents a una determinada àrea s'anomenen coeficients crítics.
Cal
examinar amb cura la configuració de la tabla de la
distribució i les gràfiques que l'acompanyen per
determinar a quina àrea es refereix cada coeficient
crític
(part de l'esquerra, interior, exterior...) i
quins són per tant els coeficients tals
que xp≤f(S,Ω)≤x1-p
ens dóna un interval de confiança per a
Ω del 100α% .
Activitat
1.29. Direm que [Ω1,Ω2]
és un interval de
confiança
del 100α% per a un paràmetre poblacional
Ω si la probabilitat de
que Ω estiga dins d'aquest interval és igual a
α. Per
determinar-ho necessitarem conèixer la
distribució
mostral d'alguna funció f(S,Ω), essent S
l'estadístic
d'una mostra que utilitzem per estimar Ω. En general,
buscarem en
aquesta distribució mostral de densitat
probabilística
dos "pics" de probabilitat p, de manera que l'àrea entre els
dos
"pics" siga α, tal com s'indica en la figura adjunta.
Observem que, per
tal com l'àrea baix de la corba és 1, s'ha
d'acomplir 2p+α=1.
Les abcises corresponents a una determinada àrea s'anomenen coeficients crítics.
Cal
examinar amb cura la configuració de la tabla de la
distribució i les gràfiques que l'acompanyen per
determinar a quina àrea es refereix cada coeficient
crític
(part de l'esquerra, interior, exterior...) i
quins són per tant els coeficients tals
que xp≤f(S,Ω)≤x1-p
ens dóna un interval de confiança per a
Ω del 100α% .
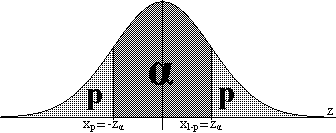 Exercici 1.7: si
les
mostres són grans (n≥30) i el paràmetre
poblacional
és la mitjana poblacional, aleshores prenent la
normalització de la mitjana de la mostra,
Exercici 1.7: si
les
mostres són grans (n≥30) i el paràmetre
poblacional
és la mitjana poblacional, aleshores prenent la
normalització de la mitjana de la mostra,
z = f( ,μ)
= (
,μ)
= ( -μ)/σ(
-μ)/σ( ),
es
distribuirà aproximadament d'acord amb la
distribució
normal tipificada. Per obtenir l'interval de confiança
haurem de
calcular primer la mitjana i la desviació típica
de la
mostra,
),
es
distribuirà aproximadament d'acord amb la
distribució
normal tipificada. Per obtenir l'interval de confiança
haurem de
calcular primer la mitjana i la desviació típica
de la
mostra,  ,
s; a continuació calcular la desviació
típica
corregida
,
s; a continuació calcular la desviació
típica
corregida  , utilitzar-la com estimador inesbiaxat de la
desviació típica poblacional σ, i a
partir del valor
estimat d'aquesta obtenir la desviació típica de
les
mitjanes en la distribució mostral, σ(
, utilitzar-la com estimador inesbiaxat de la
desviació típica poblacional σ, i a
partir del valor
estimat d'aquesta obtenir la desviació típica de
les
mitjanes en la distribució mostral, σ( ).
Utilitzant
la tabla
de la distribució normal tipificada (inversa) per
obtenir el
coeficient crític zα
tal que la
probabilitat de |z|≤zα
siga α (recordem que la
distribució normal tipificada és
simètrica) podrem averiguar l'interval de
confiança per a μ. Obtenir les
fórmules corresponents.
).
Utilitzant
la tabla
de la distribució normal tipificada (inversa) per
obtenir el
coeficient crític zα
tal que la
probabilitat de |z|≤zα
siga α (recordem que la
distribució normal tipificada és
simètrica) podrem averiguar l'interval de
confiança per a μ. Obtenir les
fórmules corresponents.
Problema 1.13:
aplicar-ho a l'obtenció d'un interval de
confiança del
80% per al número mitjà d'asos resultants de
llançar 30 vegades un dau a partir dels resultats
experimentals
obtinguts per tots els alumnes de la classe (en un número no
inferior a 30).
Activitat 1.30.
Si per consideracions teòriques formulem la
hipòtesi d'un valor per a un paràmetre
poblacional Ω, i a partir d'una mostra experimental obtenim
un interval de confiança del 100α% per a aquest
paràmetre poblacional, si el valor
teòric d'aquest està fora d'aquest interval,
és a
dir
f(S,Ω) [xp,x1-p],
poden
haver dues explicacions: la primera és que la teoria i per
tant la hipòtesi estiga equivocada; la segona és
que la mostra siga "anòmala", de manera que essent correcta
la teoria el paràmetre poblacional Ω estiga fora
de l'interval de confiança del 100α%: la
probabilitat d'això
és β=1-α. Direm així
que la mostra ens permet rebutjar la hipòtesi amb un nivell de significació
de β (que serà per tant la probabilitat de
que s'equivoquem al rebutjar la hipòtesi). Naturalment,
solament podrem rebutjar hipòtesis amb nivells de
significació iguals o menors a 0'5, i quant menor siga el
nivell de significació el rebuig de la hipòtesi
tindrà més força.
[xp,x1-p],
poden
haver dues explicacions: la primera és que la teoria i per
tant la hipòtesi estiga equivocada; la segona és
que la mostra siga "anòmala", de manera que essent correcta
la teoria el paràmetre poblacional Ω estiga fora
de l'interval de confiança del 100α%: la
probabilitat d'això
és β=1-α. Direm així
que la mostra ens permet rebutjar la hipòtesi amb un nivell de significació
de β (que serà per tant la probabilitat de
que s'equivoquem al rebutjar la hipòtesi). Naturalment,
solament podrem rebutjar hipòtesis amb nivells de
significació iguals o menors a 0'5, i quant menor siga el
nivell de significació el rebuig de la hipòtesi
tindrà més força.
Problema 1.14:
amb quin nivell de significació podríem en el seu cas
rebutjar la hipòtesi de que el dau del Problema 1.13 no
està carregat (és a dir, que totes les cares del
dau tenen la mateixa probabilitat de sortir)?
Activitat 1.31.
Si les
mostres són xicotetes, la seua distribució no
s'aproxima
a la normal. Però si una variable aleatòria X
té
una distribució normal en una població infinita,
la
distribució de l'estadístic
t = f( ,μ)
= (
,μ)
= ( -μ(X))/σ(
-μ(X))/σ( )
de les
mostres de grandària n és Yν(t)=Yν(0)·(1+t2/ν)-(ν+1)/2
amb ν=n-1, que s'anomena distribució
t de "Student" amb
ν graus de
llibertat.
Yν(0) s'escollís de manera que ∫-∞+∞
Yν(t)dt=1 .
)
de les
mostres de grandària n és Yν(t)=Yν(0)·(1+t2/ν)-(ν+1)/2
amb ν=n-1, que s'anomena distribució
t de "Student" amb
ν graus de
llibertat.
Yν(0) s'escollís de manera que ∫-∞+∞
Yν(t)dt=1 .
Tenint en compte que e = lim
u→∞ (1+1/u), demostrar el
Teorema 1.30:
lim
ν→∞ Yν(t)
= PN(0,1)(t)
(és a dir, la distribució t de "Student" s'aproxima
a la
distribució normal tipificada quan el número de
graus de
llibertat es fa
molt gran); quant valdrà Y∞(0)?
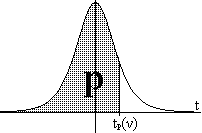 Activitat 1.32.
Utilitzarem
la tabla
de la distribució t
de "Student"
(inversa) per a
determinar el
coeficient crític tp(ν)
corresponent a
l'interval de confiança del 100α% de la mitjana
poblacional μ a
partir de la mitjana
Activitat 1.32.
Utilitzarem
la tabla
de la distribució t
de "Student"
(inversa) per a
determinar el
coeficient crític tp(ν)
corresponent a
l'interval de confiança del 100α% de la mitjana
poblacional μ a
partir de la mitjana  i la desviació
típica s(X) d'una mostra de
grandària n, amb les fórmules obtingudes en
l'Exercici
1.7.
i la desviació
típica s(X) d'una mostra de
grandària n, amb les fórmules obtingudes en
l'Exercici
1.7.
Problema 1.15:
obtenir
un interval de confiança del 90% per a la mitjana d'una
variable
aleatòria en una població infinita amb
distribució
normal a partir de la mostra
(302'23, 302'21, 302'23, 302'22, 302'25).
Activitat 1.33.
Problema 1.16:
formant
grups de 3 a 5 estudiants, cada estudiant en cada grup haurà
de
llançar 30 vegades un dau i anotar el número
d'asos
obtinguts; fer estimacions al voltant de cada dau a partir de la mostra
donada pels resultats obtinguts per cada grup.
 Activitat 1.34. Si una
variable aleatòria X té una
distribució normal en
una població infinita, la distribució de
l'estadístic
Activitat 1.34. Si una
variable aleatòria X té una
distribució normal en
una població infinita, la distribució de
l'estadístic
χ2 =
f(s,σ) = n·s(X)2/σ(X)2
de les mostres de grandària n entre 0 i ∞
és Vν(χ2)=Kν·(χ2)(ν-2)/2·e-χ2/2
amb ν=n-1, que s'anomena distribució
Khi-quadrat amb ν graus de llibertat. Kν
s'escollís de manera que
∫0∞ Vν(χ2)=1.
Utilitzarem la tabla
de la distribució Khi-quadrat (inversa) per a
determinar els
coeficients crítics χ2p(ν)
corresponents a
l'interval de confiança del 100α% de la
desviació
típica poblacional σ a
partir de la desviació típica s(X) d'una mostra
de
grandària n, de manera que χ2p(ν)
≤ χ2
≤ χ21-p(ν)
. Obtenir l'expressió per a l'interval de
confiança de la
desviació típica poblacional σ(X).
Observem que la
desviació típica corregida  (X)
de la
mostra ha d'estar necessàriament dins d'aquest interval, per
tal
com és un estimador inesbiaixat de la desviació
típica poblacional.
(X)
de la
mostra ha d'estar necessàriament dins d'aquest interval, per
tal
com és un estimador inesbiaixat de la desviació
típica poblacional.
Problema 1.17:
obtenir
un interval de confiança del 90% per a la
desviació
típica d'una variable
aleatòria en una població infinita amb
distribució
normal a partir de la mostra (302'23, 302'21, 302'23, 302'22, 302'25);
comprovar que la desviació típica corregida de la
mostra
està dins d'aquest interval.
Activitat 1.35:
Si tenim un
conjunt de k successos mutuament excloents Ei
als que suposem una probabilitat p(Ei)
per a
i=1...k, en n ocasions la freqüència esperada de
cadascú d'ells serà respectivament ei=n·p(Ei),
corresponent a la mitjana obtinguda en el Teorema 1.16. Si en una
mostra d'aquestes n ocasions les freqüències
observades
són respectivament oi, essent n≥30 i
acomplint-se ei≥5
per a tots els successos, aleshores l'estadístic χ2
= ∑i=1 k (oi-ei)2/ei
es distribuirà aproximadament d'acord amb la
distribució Khi-quadrat amb ν=k-1 graus de llibertat.
Si per a algun
succés fora ei<5
hauríem d'agregar successos fins aconseguir que s'acomplisca la
condició.
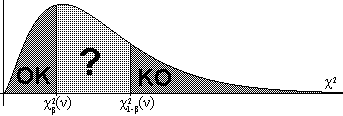 Podem utilitzar
aquest
estadístic per estimar la concordança entre la
hipòtesi probabilística i els resultats
experimentals
obtinguts en la mostra. Naturalment, quant menor siga χ2
hi haurà una major concordança: direm que hi ha bona concordança
entre la
mostra i la hipòtesi probabilística (i per
tant acceptem aquesta) amb un nivell de
significació de β si χ2<χ2β(ν);
pel contrari, si χ21-β(ν)<χ2
podrem rebutjar
la
hipòtesi probabilística amb un nivell de
significació de β (que serà de nou la
probabilitat
d'equivocar-nos al rebutjar-la, és a dir la probabilitat de
que
la hipòtesi siga correcta però hagem trobat una
mostra
entre el 100β% de les mostres més desviades de les
freqüències mitjanes esperades); finalment si
χ2β(ν)≤χ2≤χ21-β(ν)
direm que els resultats experimentals no son decisius amb aquest nivell
de significació per a acceptar o rebutjar la
hipòtesi
probabilística. Observem que una hipòtesi
probabilística pot ser acceptada (o rebutjada) amb un nivell
de
significació "feble" i els resultats no ser decisius amb un
nivell de significació més fort. El que no pot
passar
és que amb un nivell de significació acceptem una
hipòtesi i amb altre nivell de significació la
rebutgem.
Naturalment, el nivell de significació més feble
que
podem utilitzar és el de β=0'5: si χ2<χ20'5(ν)
tindrem tendència a acceptar la hipòtesis amb un
nivell
de significació major o menor, i si χ2>χ20'5(ν)
tindrem tendència a rebutjar-la.
Podem utilitzar
aquest
estadístic per estimar la concordança entre la
hipòtesi probabilística i els resultats
experimentals
obtinguts en la mostra. Naturalment, quant menor siga χ2
hi haurà una major concordança: direm que hi ha bona concordança
entre la
mostra i la hipòtesi probabilística (i per
tant acceptem aquesta) amb un nivell de
significació de β si χ2<χ2β(ν);
pel contrari, si χ21-β(ν)<χ2
podrem rebutjar
la
hipòtesi probabilística amb un nivell de
significació de β (que serà de nou la
probabilitat
d'equivocar-nos al rebutjar-la, és a dir la probabilitat de
que
la hipòtesi siga correcta però hagem trobat una
mostra
entre el 100β% de les mostres més desviades de les
freqüències mitjanes esperades); finalment si
χ2β(ν)≤χ2≤χ21-β(ν)
direm que els resultats experimentals no son decisius amb aquest nivell
de significació per a acceptar o rebutjar la
hipòtesi
probabilística. Observem que una hipòtesi
probabilística pot ser acceptada (o rebutjada) amb un nivell
de
significació "feble" i els resultats no ser decisius amb un
nivell de significació més fort. El que no pot
passar
és que amb un nivell de significació acceptem una
hipòtesi i amb altre nivell de significació la
rebutgem.
Naturalment, el nivell de significació més feble
que
podem utilitzar és el de β=0'5: si χ2<χ20'5(ν)
tindrem tendència a acceptar la hipòtesis amb un
nivell
de significació major o menor, i si χ2>χ20'5(ν)
tindrem tendència a rebutjar-la.
Problema 1.18:
contrastar la hipòtesi de que un dau no està
carregat
(que totes les cares tenen la mateixa probabilitat de sortir)
llançant-lo 30 vegades i anotant el número de
vegades que
surt cada cara.
Treball 2
(per a la seua
realització en equip):
En 100000 llançaments de 5 daus s'obté 10
repòquers, 300
pòquers, 3342 trios, 16030 parelles i 40198 simples asos. Es
podria acusar que els daus estan trucats? Amb quin nivell de
significació, en tal cas?
1.4. Obtenir una
recta
que tinga la menor
desviació possible d'un
conjunt de punts:
Objectius:
- Obtenir la recta que minimitze la suma de les desviacions quadràtiques de les ordenades d'un conjunt de punts.
- Obtenir la recta que minimitze la suma de les desviacions quadràtiques de les abscisses d'un conjunt de punts.
- Valorar el grau d'ajust de la recta de regressió al corresponent conjunt de punts.
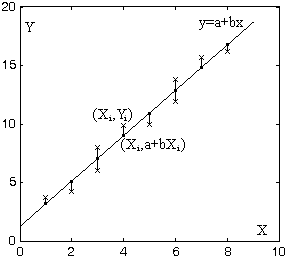 Activitat
1.36. Si tenim un conjunt de punts {Xi,
Yi}i=1...n,
direm que
y=a+bx és la recta
de regressió de Y
sobre X si i sols si
Activitat
1.36. Si tenim un conjunt de punts {Xi,
Yi}i=1...n,
direm que
y=a+bx és la recta
de regressió de Y
sobre X si i sols si ∑i=1 n (Yi-(a+bXi))2 és mínim.
Tenint el compte el
Teorema -1.8: si una funció derivable f(x,y) té un mínim en (a,b), aleshores fx'(a,b)=0 i fy'(a,b)=0
demostrar
Teorema 1.31: si y=a+bx és la recta de regressió de Y sobre X, aleshores a+b·μ(X)=μ(Y), a·μ(X)+b·μ(X2)=μ(XY).
Teorema 1.32: si y=a+bx és la recta de regressió de Y sobre X, aleshores b=cXY/σ(X)2, a=μ(Y)-b·μ(X), on cXY=μ(XY)-μ(X)·μ(Y) (covariància de X i Y).
Activitat 1.37. Tenint en compte el
Teorema -1.9: si per a una funció f(x,y) derivable fins a segon ordre s'acompleix fx'(a,b)=0, fy'(a,b)=0, fxx"(a,b)>0, fxy"(a,b)2<fxx"(a,b)·fyy"(a,b), aleshores f(x,y) té un mínim en (a,b)
demostrar el
Teorema 1.33: si σ(X)2>0, b=cXY/σ(X)2, aleshores y-μ(Y)=b·(x-μ(X)) és la recta de regressió de Y sobre X.
Observem que el "centre de masses" (μ(X),μ(Y)) pertany sempre a la recta de regressió.
Problema 1.19: obtenir la recta de regressió del número de calcer sobre l'edat en l'alumnat assistent a classe; valorar-la.
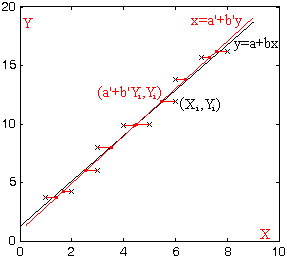 Activitat
1.38. Intercanviant la X i la Y obtenim el
Activitat
1.38. Intercanviant la X i la Y obtenim elTeorema 1.34: si σ(Y)2>0, b'=cXY/σ(Y)2, aleshores x-μ(X)=b·(y-μ(Y)) és la recta de regressió de X sobre Y.
Si σ(X)2>0 i σ(Y)2>0, ambdues rectes de regressió passaran pel "centre de masses" (μ(X),μ(Y)), i definim el coeficient de correlació de X i Y per
ρXY = cXY/(σ(X)σ(Y)) .
Demostrar
Teorema 1.35: les rectes de regressió de Y sobre X i de X sobre Y coincideixen si i sols si ρXY = ±1 .
Teorema 1.36: si ρXY = 0, aleshores les rectes de regressió són y=μ(Y) , x=μ(X) (perpendiculars).
Activitat 1.39. Direm que dues variables aleatòries X, Y no tenen correlació lineal si i sols si ρXY=0; aquesta condició és equivalent a la de cXY=0 amb σ(X)>0 i σ(Y)>0.
 Demostrar el
Demostrar elTeorema 1.36: si dues variables aleatòries són independents, no tenen correlació lineal.
La recíproca és certa? Comprovar-ho en el següent
| Problema 1.20:
estudiar la
correlació lineal en el cas |
|
X i Y són independents? |
Activitat 1.40. Demostrar
Teorema 1.37: σ(X±Y)2 = σ(X)2 + σ(Y)2 ± 2·cXY .
Teorema 1.38: si X,Y són independents o simplement no tenen correlació lineal, aleshores σ(X±Y)2 = σ(X)2 + σ(Y)2 .
Activitat 1.41. Demostrar, utilitzant el Teorema 1.37,
Teorema 1.39: Si y=a+bx és la recta de regressió de Y sobre X, aleshores σ(Y-bX)2 = σ(Y)2(1-ρXY2) .
Teorema 1.40: -1 ≤ ρXY ≤ 1 .
Si ρXY>0 direm que X,Y tenen correlació lineal positiva; si ρXY<0, direm que X,Y tenen correlació lineal negativa; si |ρXY|≈1, direm que X,Y tenen bona correlació lineal; si ρXY≈0, direm que X,Y tenen mala correlació lineal.
Problema 1.21: estudiar la correlació lineal entre el número de calcer i l'edat de l'alumnat assistent a classe; valorar-la.
1.5. Estimar si un conjunt de mostres pertanyen a la mateixa població:
Objectius:
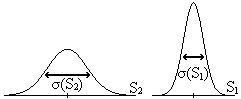
- Obtenir un estimador inesbiaixat de la variància poblacional a partir de la mitjana de les variances d'un conjunt de mostres.
- Obtenir un estimador inesbiaixat de la variància poblacional a partir de la variància de les mitjanes d'un conjunt de mostres pertanyents a la mateixa població.
- Avaluar per anàlisi de variància si un conjunt de mostres independents pertanyen a la mateixa població.
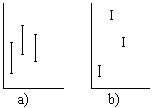 Activitat 1.42. Si tenim un
conjunt de mostres independents obtingudes per diferents procediments,
en cas que aquests procediments siguen equivalents la
dispersió
entre les mostres haurà de ser proporcionada a la
dispersió dins de cada mostra (figura a). Per tal de
avaluar-ho,
treballarem amb m mostres de grandària n i anomenarem:
Activitat 1.42. Si tenim un
conjunt de mostres independents obtingudes per diferents procediments,
en cas que aquests procediments siguen equivalents la
dispersió
entre les mostres haurà de ser proporcionada a la
dispersió dins de cada mostra (figura a). Per tal de
avaluar-ho,
treballarem amb m mostres de grandària n i anomenarem:Xjk a l'element k de la mostra j
 j
i s(Xj)2
respectivament a la mitjana i la variància de la mostra j
j
i s(Xj)2
respectivament a la mitjana i la variància de la mostra j a la
mitjana de la mostra de grandària m·n resultant
de
mesclar les m mostres de grandària n.
a la
mitjana de la mostra de grandària m·n resultant
de
mesclar les m mostres de grandària n.Demostrar el
Teorema 1.41:
 = ∑
j
= ∑
j  j/m
.
j/m
.Activitat 1.43. Anomenarem variància dintre de variables a la mitjana de les variances sw2 = ∑ j s(Xj)2/m .
Suposarem que totes les mostres pertanyen a poblacions si més no amb la mateixa variància σ2 .
Demostrar el
Teorema 1.42: μ(sw2) = σ2·(n-1)/n .
Anomenarem per tant variància corregida dintre de variables a
 w2
= sw2·n/(n-1),
la qual
serà un estimador inesbiaixat de la variància
poblacional σ2
.
w2
= sw2·n/(n-1),
la qual
serà un estimador inesbiaixat de la variància
poblacional σ2
.Activitat 1.44. Tenint en compte el
Teorema 1.43: si les variables aleatòries independents Y1, Y2 tenen distribució Khi-quadrat amb graus de llibertat ν1 i ν2 respectivament, aleshores la variable aleatòria Y1+Y2 té distribució Khi-quadrat amb ν1+ν2 graus de llibertat
demostrar el
Teorema 1.44: mn·sw2/σ2 té distribució Khi-quadrat amb m·(n-1) graus de llibertat.
Activitat 1.45. Anomenarem
μj=μ(Xj) a la mitjana de la població a la qual pertany la mostra j
μ=μ(X) a la mitjana de la població resultant de mesclar les poblacions a les quals pertanyen les m mostres
αj=μj-μ para cada mostra j (naturalment, valdrà 0 si totes les mostres pertanyen a la mateixa població).
Demostrar que en qualsevol cas s'acompleix el
Teorema 1.45: ∑ j αj = 0 .
Activitat 1.46. Anomenarem variància entre variables a la variància de les mitjanes
sb2 = ∑ j (
 j-
j- )2/m
= ∑ j
)2/m
= ∑ j  j2/m
-
j2/m
-  2
.
2
.Recordant de l'Activitat 1.26 que σ(
 j)2=σ2/n
, σ(
j)2=σ2/n
, σ( )2=σ2/(mn),
demostrar
)2=σ2/(mn),
demostrarTeorema 1.46: μ(
 j2)
= σ2/n +
(μ+αj)2
j2)
= σ2/n +
(μ+αj)2Teorema 1.47: μ(
 2)
= σ2/(mn) +
μ2
2)
= σ2/(mn) +
μ2Teorema 1.48: μ(sb2) = σ2(m-1)/(mn) + ∑ j αj2/m .
Activitat 1.47. Anomenarem variància corregida entre variables a
 b2
= sb2·nm/(m-1)
.
b2
= sb2·nm/(m-1)
.Demostrar el
Teorema 1.49: μ(
 b2)
= σ2 +
n·∑ j αj2/(m-1)
.
b2)
= σ2 +
n·∑ j αj2/(m-1)
.Per tant,
 b2
serà un estimador inesbiaixat de la variància
poblacional σ2
si i sols si les poblacions a les quals pertanyen les diferents mostres
tenen totes la mateixa mitjana (el que anomenem hipòtesi
nul·la en la
qual tot αj=0),
cosa que naturalment
passarà si totes les mostres pertanyen a la mateixa
població. En aquest cas, F=
b2
serà un estimador inesbiaixat de la variància
poblacional σ2
si i sols si les poblacions a les quals pertanyen les diferents mostres
tenen totes la mateixa mitjana (el que anomenem hipòtesi
nul·la en la
qual tot αj=0),
cosa que naturalment
passarà si totes les mostres pertanyen a la mateixa
població. En aquest cas, F= b2/
b2/ w2
haurà de ser proper a la unitat. En altre cas μ(
w2
haurà de ser proper a la unitat. En altre cas μ( b2)>σ2
, i per tant es pot preveure que F siga major que la unitat.
b2)>σ2
, i per tant es pot preveure que F siga major que la unitat.Activitat 1.48. Tenint en compte que sb2 és la variància de la mostra (
 1,
1,
 2,...
2,... m),
de grandària m, i que σ(
m),
de grandària m, i que σ( j)2=σ2/n,
demostrar que si les mostres pertanyen a la mateixa població
s'acompleix el
j)2=σ2/n,
demostrar que si les mostres pertanyen a la mateixa població
s'acompleix elTeorema 1.50: mn·sb2/σ2 té distribució Khi-quadrat amb m-1 graus de llibertat.
Activitat 1.49. Tenint el compte el
Teorema 1.51: si les variables aleatòries independents Y1, Y2 tenen distribució Khi-quadrat amb graus de llibertat ν1 i ν2 respectivament, aleshores la distribució de F=(Y1/ν1)/(Y2/ν2) entre 0 i ∞ és
Wν1,ν2(F) = Kν1,ν2·Fν1/2-1/(1+ν1·F/ν2)(ν1+ν2)/2, que s'anomena distribució F de Snedecor amb graus de llibertat ν1 i ν2 . Kν1,ν2 s'escollís de manera que ∫0∞ Wν1,ν2(F) dF = 1
demostrar el
Teorema 1.52: si tenim m mostres independents de grandària n pertanyents a la mateixa població, aleshores
F=
 b2/
b2/ w2
té una distribució F de Snedecor amb graus de
llibertat ν1=m-1,
ν2=m·(n-1)
.
w2
té una distribució F de Snedecor amb graus de
llibertat ν1=m-1,
ν2=m·(n-1)
.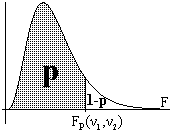 Activitat
1.50. Si tenim m mostres independents de
grandària n i
Activitat
1.50. Si tenim m mostres independents de
grandària n i F=
 b2/
b2/ w2
> Fp(m-1,
m·(n-1)), essent Fp(ν1, ν2)
el coeficient crític de la distribució F de
Snedecor amb graus de llibertat ν1
i ν2 tal
que la probabilitat d'un valor menor o igual a aquest coeficient siga
p, aleshores podem rebutjar amb un nivell de significació
β=1-p la hipòtesis nul·la de que les
mostres pertanguen a la mateixa població. Utilitzarem les tables
de la distribució F de Snedecor (inversa) per
determinar el corresponent coeficient crític.
w2
> Fp(m-1,
m·(n-1)), essent Fp(ν1, ν2)
el coeficient crític de la distribució F de
Snedecor amb graus de llibertat ν1
i ν2 tal
que la probabilitat d'un valor menor o igual a aquest coeficient siga
p, aleshores podem rebutjar amb un nivell de significació
β=1-p la hipòtesis nul·la de que les
mostres pertanguen a la mateixa població. Utilitzarem les tables
de la distribució F de Snedecor (inversa) per
determinar el corresponent coeficient crític.Problema 1.22: anotar el número de calcer en vàries mostres de la mateixa grandària entre l'alumnat assistent a classe i valorar si pertanyen a la mateixa població (a ser possible, procurar que alguna de les mostres estiga formada únicament per xics i altra únicament per xiques).
Activitat 1.51. Com hauríem d'interpretar el fet que F=
 b2/
b2/ w2
<< 1? Aplicar-ho a la resolució del
següent
w2
<< 1? Aplicar-ho a la resolució del
següentProblema 1.23: calcular l'estadístic F corresponent al següent parell de mostres:
X1=(24'2, 25'3, 25'4, 26'2, 27'5)
X2=(24'2, 25'3, 25'4, 26'2, 27'4)
Es pot considerar que les mostres no acomplisquen alguna de les premises del Teorema 1.52?
Per a valorar-ho amb un cert nivell de significació podem utilitzar la relació Fp(ν1, ν2)=1/F1-p(ν2, ν1) .
Treball 3 (per a la seua realització en equip):
Comparar diferents procediments per a obtenir algun preparat químic utilitzant alguna variable aleatòria adequada (quantitat del preparat, temps per a la seua obtenció, etc.). Obtenir les dades d'experiències reals i utilitzar un mínim de 3 procediments aplicant com a mínim 5 vegades cada procediment. Estimar per anàlisi de variància si els diferents procediments es poden considerar equivalents.
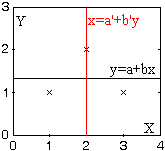
Activitat 1.1: Debatir en grups menuts el següent text, escollint prèviament un portaveu de cada grup per exposar posteriorment les conclusions i en el seu cas les dubtes suscitades:
Des de Leibnitz i Newton, s'ha desenvolupat fonamentalment la matemàtica contínua. Això anava acompanyat d'una concepció del món segons la qual les variables reals variarien de forma contínua, però responia també a raons pràctiques: el tractament de variables discretes exigeix un gran número de càlculs per als quals no es disposava d'instruments adequats, mentre que sí es disposava de poderosos mètodes analítics, de càlcul diferencial i integral, per al tractament de variables contínues. Tanmateix, hi havia un gran número de problemes que no es podien resoldre amb aquestos mètodes analítics.
Tanmateix, actualment la situació ha canviat radicalment: per una banda, es reconeix, amb una forta fonamentació en la mecànica quàntica, que, donades les limitacions en la precisió de les dades experimentals, sempre treballem realment amb variables discretes; i per altra banda, l'ús dels ordinadors permet la realització dels càlculs massius necessaris per al tractament d'aquestes variables discretes.
El càlcul numèric consisteix en una sèrie de mètodes per obtindre aproximacions discretes a la solució de diferents problemes.
Així, si tenim els valors de f(xi) per a determinats valors de xi, buscarem aproximar per interpolació el valor de f(x) per a un nou valor de x; es poden utilitzar diferents funcions d'interpolació, depenent de l'estimació que es faça de les característiques de f(x); en aquest curs aproximarem únicament mitjançant funcions polinòmiques, fent el que s'anomena interpolació polinòmica. Però si el nou valor de x es troba fora de l'interval delimitat pels xi prèviament estudiats, estarem fent realment una extrapolació: l'aproximació polinòmica de f(x) ens donarà aleshores una hipòtesi a contrastar amb noves dades.
Igualment, hi ha molts problemes d'integració que no es poden resoldre de forma analítica, és a dir, no podem obtenir una funció integral contínua y=F(x) la derivada de la qual satisfaga les condicions del problema. Però podrem tanmateix trobar solucions aproximades del seu valor numèric per a valors particulars de x.
2.1. Interpolar el valor d'una funció polinòmica desconeguda que passe per un conjunt de punts:
Objectius:
- Demostrar l'existència i unicitat del polinomi interpolador de grau menor o igual que m que passa per m+1 punts d'abscisses distintes.
- Trobar una fórmula que ens done directament l'expressió del polinomi interpolador.
- Trobar un mètode per a obtenir successivament punts interpolats a mesura que introduïm nous punts per a interpolar.
- Trobar un mètode que ens done successius
termes del polinomi interpolador.
- Entendre els problemes de fiabilitat
de la interpolació, especialment si es realitza fora de
l'interval en el qual es tenen dades (extrapolació) o
s'utilitzen
polinomis d'un grau elevat.
Teorema -2.1: |xki| = ∏ k>i (xk-xi)
i la
Definició 2.1: direm que p(x) = ∑ i=0 m ai xi és un polinomi interpolador de grau menor o igual que m en els punts
{(xk,fk) / k=0,1...m} si i només si, per a tot k=0,1...m, p(xk)=fk ,
demostrar el
Teorema 2.1: si per a tot i≠k, xi≠xk, llavors existeix un únic polinomi interpolador de grau menor o igual que m en els punts {(xk,fk) / k=0,1...m} .
Activitat 2.3. Tenint en compte que
∑ i=0 m Ξi = Ξk + ∑ i≠k Ξi per a tot k=0,1...m, i que
∏ j≠i Ξkj = Ξkk·∏ j≠i & j≠k Ξkj per a tot i≠k.
demostrar el
| Teorema 2.2: si per a tot i≠k, xi≠xk, llavors p(x) = ∑ i=0 m fi | ∏
j≠i (x-xj) ∏ j≠i (xi-xj) |
Activitat 2.4.
Problema 2.1: donats els punts
| x
k. |
1. |
2. |
4. |
5. |
| f
k |
0. |
2. |
12. |
21. |
(suggeriment: a l'aplicar la fórmula, escriure primer cada denominador per a evitar errors)
Activitat 2.5. Demostrar el
Teorema 2.3: si per a tot i,j=0,1...m, si i≠k, llavors xi≠xk,
& si i+j≤m , llavors pi,j és el polinomi interpolador de grau menor o igual que j en {(xk,fk) / k=i,i+1...i+j},
llavors per a tot j=1...m, i=0,1...m-j,
| pi,j(x)
= |
(xi+j-x)pi,j-1
+ (x-xi)pi+1,j-1. xi+j - xi |
Activitat 2.6. Tenint en compte que, amb els pi,j definits en el Teorema 22,
Teorema 2.4: per a tot i=0,1...m & per a tot xcR, pi,0(x) = f i
i
Teorema 2.5: p0,m és el polinomi interpolador de grau menor o igual que m en {(xk,fk) / k=0,1...m} ,
utililizar l'algorisme
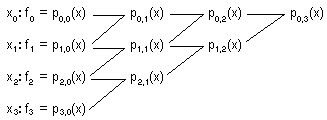 (mètode
de Neville)
(mètode
de Neville)per a resoldre el
Problema 2.2: donats els punts
| x
k |
1. |
2. |
4. |
| f
k |
0. |
2. |
12. |
Afegir a continuació el punt (x3, f3) = (5, 21) i obtenir la nova interpolació per a x=3 .
Comparar el resultat obtingut amb el del problema 2.1.
Activitat 2.7. D'acord amb la
Definició 2.2: amb {(xk,fk) / k=0,1...m} tal que per a tot i,j=0,1...m, si i≠k, llavors xi≠xk, definirem les diferències dividides f[xi,xi+1,...xj] mitjançant| f[xi]
= |
fi | per a
tot
i=0,1...m |
| f[xi,xi+1,xj]
= |
f[xi+1,...xj]
- f[xi,...xj-1] xj - xi |
per a
tot i=0,1...m-1
, j=i+1,...m |
| f[x0] f[x1] f[x2] f[x3] |
> f[x0,x1] > f[x1,x2] > f[x2,x3] |
>
f[x0,x1,x2] > f[x1,x2,x3] |
>
f[x0,x1,x2,x3] |
| k. |
0. |
1. |
2. |
3. |
| x
k |
1. |
2. |
4. |
5. |
| f
k |
0. |
2. |
12. |
21. |
pm(x) = ∑j=0 m f[x0,...xj] ∏i=0 j-1 (x-xi)
és el polinomi interpolador de grau menor o igual que m en {(xk,fk) / k=0,1...m} (mètode de Newton)
Activitat 2.8. Assumint que l'error de la interpolació polinòmica de grau menor o igual que m ve donada per
Teorema -2.2: f(x)-pm(x) = [f (m+1)(ξ(x))/(m+1)!] ∏i=0 m (x-xi) tal que ξ(x)c[a,b] tal que per a tot i=0,1...m, xic[a,b]
Problema 2.4: fitar el valor de f(3) suposant que
| x
k |
1. |
2. |
4. |
5. |
| f(x
k) |
0. |
2. |
12. |
21. |
2.2. Aproximar la integració d'una funció, acotant l'error d'aproximació:
Objectius:
- Obtenir uns pesos Wk independents de la funció f(x) tals que sumant el seu producte pels corresponents valors de la funció en determinats nodes xk, ∑ k=0 m Wk f(xk), proporcione la integral exacta per a polinomis fins a un cert grau, i una bona aproximació per a altres funcions.
- Aprendre a fitar l'error d'aquesta aproximació expressant-lo com el producte d'un factor C independent de la funció f(x) per la derivada d'un cert ordre r de la funció en algun punt ξ de l'interval d'integració [a,b] , Cf(r)(ξ).
- Estudiar el cas de nodes equidistants, xk=a+kh (Fórmula de Newton-Cotes).
- Aprendre a millorar l'aproximació augmentant el nombre de nodes.
- Utilitzar el mètode de coeficients indeterminats per a obtenir tant els pesos Wk d'integració com el factor C de l'error, a partir de la integral exacta de potències simples i resolent en grups menuts els corresponents sistemes d'equacions per a exposar públicament a continuació els resultats obtinguts.
Definició 2.3: essent f:[a,b]→R una funció integrable, anomenarem integral numèrica polinòmica de f en els nodes xk tals que a≤x0<...<xm≤b a la integral en l'interval [a,b] del polinomi interpolador de grau menor o igual que m en els punts {(xk,f(xk)}k=0,1...m
i utilitzant l'expressió del polinomi interpolador proporcionada pel mètode de Lagrange, justificar l'existència d'uns pesos Wk independents de la funció f(x) amb els quals ∑ k=0 m Wk f(xk) siga la seua integral numèrica polinòmica.
Activitat 2.10. Tenint en compte que una integral numèrica polinòmica en m+1 nodes és igual a la integral exacta per a polinomis de grau menor o igual que m, trobar un sistema d'equacions per a l'obtenció dels pesos Wk i demostrar que si per a tot i≠k, xi≠xk, aquest sistema d'equacions té solució única.
Teorema -2.3: ∫a b f(x) dx = ∫u-1(a) u-1(b) f(u(t)) u'dt
demostrar el
Teorema 2.6: en el cas de nodes equidistants x k=a+kh, amb k=0,1...m, h=(b-a)/m, demostrar que els pesos per al càlcul de la corresponent integral numèrica polinòmica (pesos de Newton-Cotes) tenen la forma Wk=hW'k(m), on W'k(m), que són els pesos corresponents al cas h=1, només depenen de k i de m (però no de a i de b ).
Pot utilitzar-se per a la demostració l'expressió dels pesos Wk obtinguda en l'Activitat 2.9, aplicant en la corresponent integral el canvi de variable x=a+th .
Activitat 2.12. Obtenir els pesos de Newton-Cotes per a m=2 i l'interval [0,2]. A partir dels mateixos, obtenir la fórmula general (Fórmula de Simpson) per a la integral numèrica polinòmica en els nodes {a, a+h, a+2h} = {a, (a+b)/2, b},
S =
Activitat 2.13.
Problema 2.5: aproximar mitjançant la Fórmula de Simpson ∫-1 1 e x2 dx .
Activitat 2.14. Tenint en compte l'expressió de l'error de la interpolació polinòmica de grau menor o igual que m donada pel Teorema -2.2 , així com que
Teorema
-2.4: per a
tota
funció integrable f:[a,b]→R, |∫a b
f(x)dx|
≤ ∫a b |f(x)|dx .
Teorema -2.5:
per a
tot
parell de funcions integrables f:[a,b]→R, g:[a,b]→R+,
existeix ξc[a,b]
tal
que
demostrar el
Teorema 2.7: el valor absolut de l'error de la integral numèrica polinòmica en m+1 nodes pot fitar-se pel producte de dos factors, un dels quals depèn únicament dels nodes, i l'altre depèn únicament de la derivada d'ordre m+1 en algun punt ξ de l'interval d'integració [a,b].
Activitat 2.15. Suposant que l'error d'un mètode d'integració aproximada siga de la forma
NOTA: en cas d'obtenir-se C=0 pot inferir-se que el mètode és exacte per a aquesta funció, i haurà de repetir-se el procés substituint r per r+1 .
Activitat 2.16.
Tenint
en compte el
| Teorema -2.6:
per a tot fcC
r(R→R),
xcC1(R→R),
|
dr f
dtr |
(x(t)) = ﴾dx/dt﴿r
|
dr f
dxr |
(x) |
Teorema 2.8: si l'expressió de l'error per a aproximar ∫0 m f(t)dt amb nodes equidistants i h=1 és
| ε' = C' | dr f dtr |
(ζ) per
a algun ζc[0,m], |
| ε = C. | dr f dxr |
(ξ) per a algun ξc[a,b] amb C=hr+1 C' |
Activitat 2.17. Obtenir l'expressió de l'error per a la Fórmula de Simpson per a l'interval [0,2] (amb h=1), i a partir d'ella obtenir l'expressió general de l'error per a la Fórmula de Simpson per a l'interval [a,b] (amb h=(b-a)/2),
εS =
Indicar per a quins polinomis serà exacta aquesta fórmula.
Activitat 2.18.
Problema 2.6: fitar l'error de la Fórmula de Simpson aplicada a ∫-1 1 e x2 dx . Valorar-lo.
Activitat 2.19. Tenint en compte la
Definició 2.4: essent f:[a,b]→R una funció integrable, anomenarem integral numèrica composta de grau m en els mM+1 nodes {a+kh}k=0,1...mM , amb h=(b-a)/(mM), a.
demostrar el
Teorema 2.9: per a tota funció integrable f:[a,b]→R , la seua integral numèrica composta de grau 2 en els 2M+1 nodes {a+kh}k=0,1...2M , amb h=(b-a)/(2M), (regla de Simpson) ve donada per
= [f(a) + f(b) + ∑i=1 M-1 2f(a+2ih) + ∑i=0 M-1 N4f(s+(2i+1)h)](b-a)/(6M)
Activitat 2.20. Tenint en compte el
Teorema -2.7: per a tota funció contínua f:[a,b]→R i tot conjunt de punts ξ ic[a,b], i=1...n, existeix ξc[a,b] tal que
Teorema 2.10: per a tota fcC4([a,b],R), l'error de la regla de Simpson per aproximar ∫a b f(x)dx ve donat per
Activitat 2.21.
Problema 2.7: quin increment h hauríem de prendre per a obtenir una aproximació a ∫-1 1 e x2 dx amb un error menor a 0'01 mitjançant la regla de Simpson?
 Treball 4
(per a
la seua realització en equip):
Treball 4
(per a
la seua realització en equip):Obtenir els coeficients W0, W1 que fan que
Utilitzar-ho per a fitar ∫0 10 (225+x3)½dx sabent que |f "(x)|<0'6 en aquest interval.
2.3. Obtenir el valor futur d'una variable coneixent el seu valor inicial y la dependència de la seua derivada respecte del temps i la mateixa variable, y'=f(t,y):
Objectius:
- Aproximar solucions d'una equació diferencial a partir d'unes condiciones inicials substituint l'increment per la diferencial (MÈTODE D'EULER).
- Obtenir una aproximació de segon ordre a les solucions d'una equació diferencial (MÈTODE DE RUNGE).
- Generalitzar la Fòrmula de Simpson per a integrar equacions diferencials (MÈTODE DE RUNGE-SIMPSON).
- Obtenir una aproximació de quart ordre a les solucions d'una equació diferencial (MÈTODE DE KUTTA).
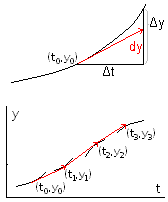 Activitat
2.22. Si coneguem y'=f(t,y) així com la condició
inicial y0=y(t0),
tenint en compte el
Activitat
2.22. Si coneguem y'=f(t,y) així com la condició
inicial y0=y(t0),
tenint en compte elTeorema -2.8: si y(t) és una funció derivable fins al segon ordre,
y(t) = y(t0) + y'(t0)·∆t + y"(ξ)·(∆t)2/2 tal que ξc[t0, t]
s'acomplirà y(t) = y0 + f(t0,y0)·∆t + Θ·(∆t)2 . Així doncs, si substituïm ∆y=y(t)-y0 per dy=y'·∆t=f(t0,y0)·∆t l'error serà proporcional a (∆t)2, i si ∆t és suficientment xicotet podrem aproximar l'evolució de la variable y aplicant successivament
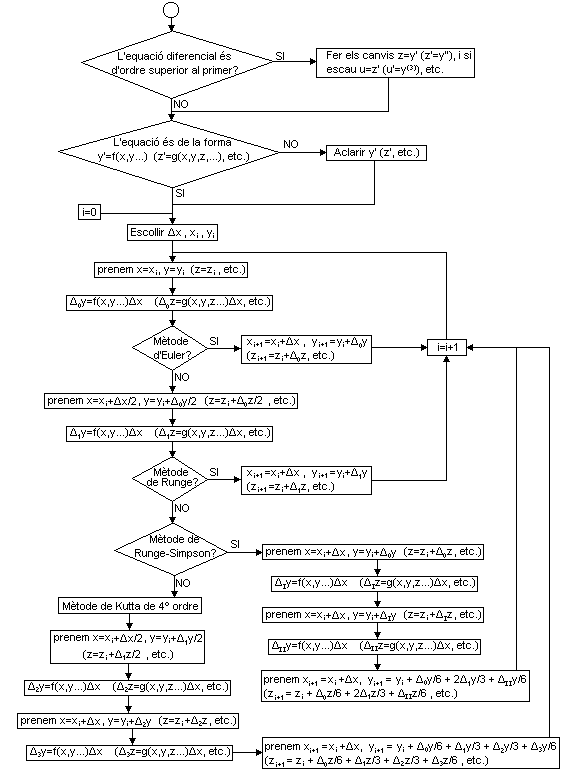
ti+1=ti+∆t , yi+1 = yi + ∆0y amb ∆0y=f(ti,yi)·∆t (mètode d'Euler).
Problema 2.8: aplicar el mètode d'Euler per aproximar el valor de y quan t=1 coneixent que y=1 quan t=0 i que y'=0'1y2-ty. Prendre ∆t=0'2 i representar-ho gràficament.
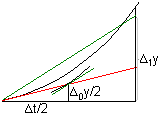 Activitat
2.23.
El mètode d'Euler donaria un resultat exacte si la derivada y',
representada per la pendent de la corba, fora constant (i per tant la
segona derivada valguera zero). Si no és així, trobarem
que la derivada
en el punt (t1,y1)
serà f(t1,y1)=f(t0+∆t,y0+∆0y)≠f(t0,y0).
En aquest cas, podem obtenir una millor aproximació si calculem
la derivada en el punt intermedi (t0+∆t/2,y0+∆0y/2)
i prenem y1=y0+∆1y
amb ∆1y=f(t0+∆t/2,y0+∆0y/2)·∆t,
i així successivament (mètode
de Runge de segon ordre); en aquest cas l'error és
proporcional a (∆t)3 .
Activitat
2.23.
El mètode d'Euler donaria un resultat exacte si la derivada y',
representada per la pendent de la corba, fora constant (i per tant la
segona derivada valguera zero). Si no és així, trobarem
que la derivada
en el punt (t1,y1)
serà f(t1,y1)=f(t0+∆t,y0+∆0y)≠f(t0,y0).
En aquest cas, podem obtenir una millor aproximació si calculem
la derivada en el punt intermedi (t0+∆t/2,y0+∆0y/2)
i prenem y1=y0+∆1y
amb ∆1y=f(t0+∆t/2,y0+∆0y/2)·∆t,
i així successivament (mètode
de Runge de segon ordre); en aquest cas l'error és
proporcional a (∆t)3 .Problema 2.9: aplicar el mètode de Runge de segon ordre per aproximar el valor de y quan t=0'4 coneixent que y=1 quan t=0 i que y'=0'1y2-ty. Prendre ∆t=0'2.
Activitat 2.24. Amb el mètode de Runge de segon ordre hem millorat l'aproximació calculant un nou increment per a la funció y a partir d'un punt auxiliar (en aquest cas, intermedi). Podem obtenir millors aproximacions escollint successivament de forma adequada nous punts auxiliars. En particular, si prenem successivament
∆Iy=f(t0+∆t, y0+∆0y)·∆t
∆IIy=f(t0+∆t, y0+∆Iy)·∆t
obtindrem una aproximació de tercer ordre, amb error proporcional a (∆t)4, si prenem
t1=t0+∆t, y1 = y0 + ∆0y/6 + 4·∆1y/6 + ∆IIy/6 i així successivament (mètode de Runge-Simpson).
Comprovar que en el cas particular en que tinguem y'=f(x), aquest mètode és equivalent a la Fórmula de Simpson.
Activitat 2.25. Podem obtenir una aproximació de quart ordre, amb error proporcional a (∆t)5, si prenem
∆2y=f(t0+∆t/2,y0+∆1y/2)·∆t
∆3y=f(t0+∆t, y0+∆2y)·∆t
i finalment
t1=t0+∆t, y1 = y0 + ∆0y/6 + ∆1y/3 + ∆2y/3 + ∆3y/6 i així successivament (mètode de Kutta de quart ordre).
Tenim recopilats els diferents mètodes en el següent diagrama de fluixos:
Podem utilitzar també el següent diagrama per tal de recordar a partir de quin increment s'obté un nou increment (amb increment total o amb mig increment) i quins coeficients hem d'utilitzar per obtenir l'increment final:
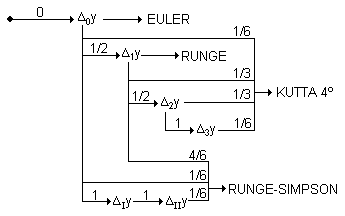
Per al mètode de Kutta de quart ordre podem realitzar els càlculs en la següent tabla:
| ti yi |
t0 y0 |
t1
= t0+∆t y1 = y0 + ∆0y/6 + ∆1y/3 + ∆2y/3 + ∆3y/6 |
|||
| t y y' ∆0y ∆1y ∆2y ∆3y |
t0 y0 f(t,y) ∆0y |
t0+∆t/2 y0+∆0y/2 f(t,y) ∆1y |
t0+∆t/2 y0+∆1y/2 f(t,y) ∆2y |
t0+∆t y0+∆2y f(t,y) ∆3y |
|
Naturalment, alhora d'aplicar les tables les expressions es substitueixen per números.
Problema 2.10: aplicar el mètode de Kutta de quart ordre per aproximar el valor de y quan t=0'6 coneixent que y=1 quan t=0 i que y'=0'1y2-ty. Prendre ∆t=0'2.