Licenciatura en Ciencias Químicas
GUÍA DIDÁCTICA
Rafael Pla López
Departamento de Matemática Aplicada
Universitat de València
curso 2008-2009.
Objetivos:
Específicos:
- Determinar
el error del resultado de un cálculo a partir del
error de los datos de los cuales partimos (PROPAGACIÓN
DE ERRORES).
- Inferir información sobre poblaciones a partir de una porción de las mismas (INTRODUCCIÓN A LA ESTADÍSTICA).
- Aprender a obtener medidas de centralización y dispersión en una distribución estadística.
- Estudiar casos
típicos de distribuciones
estadísticas de probabilidades.
- Hacer estimaciones sobre una población a partir de una muestra.
- Obtener una recta que tenga la menor desviación posible de un conjunto de puntos.
- Estimar si un conjunto de muestras
pertenecen a la misma
población.
- Obtener aproximaciones discretas a la solución de diferentes problemas (INTRODUCCIÓN AL CÁLCULO NUMÉRICO).
- Interpolar el valor de una función polinómica desconocida que pase por un conjunto de puntos.
- Aproximar la integración de una función, acotando el error de aproximación.
- Obtener el valor futuro de una variable conociendo su valor inicial y la dependencia de su derivada respecto del tiempo y la misma variable, y'=f(t,y).
- Aprender a utilizar un lenguaje de programación o un paquete informático, a elección del profesorado de cada grupo de prácticas.
- Aprender a trabajar en equipo.
- Aprender a exponer públicamente un trabajo.
- Adquirir respeto por los compañeros que exponen un trabajo, atendiéndolos y ayudándolos en caso necesario.
- Aprender a realizar razonamientos deductivos para demostrar un enunciado a partir de determinadas premisas.
- Adquirir la capacidad de cuestionar la fiabilidad de los resultados obtenidos por métodos numéricos y estadísticos
- Trabajo en clase en grupos pequeños debatiendo textos, demostrando enunciados y resolviendo problemas, seguido de su exposición pública.
- Trabajo en equipo fuera de clase, elaborando trabajos para su presentación al profesor.
- Trabajo práctico en aula de informática.
- La calificación final será la media de la nota de teoría y la nota de prácticas, siempre que ambas sean igual o superior a 4 (sobre un máximo de 10).
- Para la nota de teoría puntuará hasta 8 puntos la evaluación de un examen final individual escrito, y hasta 2 puntos la realización de trabajos en equipo, que solamente podrán considerarse en caso de asistencia regular a clase (de lo contrario, deberán responderse cuestiones adicionales en el examen final puntuables hasta los 2 puntos restantes). Se podrá consultar esta Guía Didáctica y un formulario escrito a mano personalmente en un máximo de 3 hojas sin problemas resueltos (no se admiten fotocopias). Además, se primará la participación activa en clase sumando una dècima por cada exposición pública de un trabajo realizado en clase.
- La nota de prácticas se determinará
por
la evaluación de las memorias presentadas de las
prácticas realizadas y de la evaluación de un
examen
práctico individual en ordenador, el cual puntuará
entre
el 40 y el
60% de la nota de prácticas (porcentaje a determinar por el
profesorado de cada grupo de prácticas).
Bibliografía:
Estadística:
- Canavos, G.C. (1987), Probabilidad y Estadística. Aplicaciones y Métodos, McGrawHill
- Christensen, M.B. (1983), Estadística paso a paso, Trilla, Mexico
- Cuadras, C.M. (1986), Problemas de Probabilidad y Estadística, Anaya, Madrid
- Dwnie, N.M., Heath, R.W. (1971), Métodos de Estadística Aplicada, Ed.del Castillo, Madrid
- Dowdy, S., Wearden, S. (1991), Statistics for Research, Wiley & sonidos
- Fz.de Troconiz, A. (1987), Probabilidades, Estadística, Muestreo, Ed.Tébar Flores, Madrid
- Gmurman, V.E. (1974), Teoría y Problemas. Estadística Matemática, Mir, Moscu
- Gutiérrez, S. (1976), Estadística Aplicada, ed.facsímil, València
- Gutiérrez Cabría, S., Probabilidades, Bioestadística, Ed.Tebar Flores, Madrid
- Haber, A., Runyon, R.P. (1973), Estadística General, Fondo Educativo Iberoamericano
- Labrousse, C. (1968), Estadística, Colección Univ.de Matemática Pura, Madrid
- Martínez Salas, HJ. (1989), Métodos Matemáticos, Ed.el autor, Valladolid
- Mendenhall, W., Scheaffer, R.L., Wackely, D.D . (1986), Estadística Matemática con Aplicaciones, Grupo Editorial Iberoamérica
- Milton, T. (1987), Estadística para Biología y Ciencias de la Salud, InteramericanaMcGrawHill
- Ortle, B. (1970), Estadística Aplicada, LinusaWiley, Mexico
- Quesada, V., Isidoro, A., Löpez, L.A . (1984), Curso y Ejercicios de Estadística, Alhambra Universidad
- Sachs, I. (1978), Estadística Aplicada, Labor, Barcelona
- Spiegel, M.R. (1979), Estadística, Schaum/McGrawHill, México
- Spiegel, M.R. (1976), Probabilidad y estadística, Schaum/McGrawHill, México
- Williams, B. (1993), Biostatistic, Chapman & Hall
Cálculo Numérico:
- Aubanell, A., Benseny, A., Delshams, A. (1991), Eines bàsiques de Càlcul Numèric, Universitat Autònoma de Barcelona , Bellaterra
- Aubanell, A., Benseny, A., Delshams, A. (1993), Útiles básicos de Cálculo Numérico, Editorial Labor, Barcelona
- Chapra, S.C., Canale, R.P. (1985), Métodos numéricos para ingenieros (cono aplicaciones en computadoras personales), McGrawHill, Mexico
- Cuento, S.D., Boor, C.de (1974), Análisis numérico elemental, McGrawHill, México
- Cordero, A., Hueso, J.L, Martínez, E., Torregrosa, J.M. (2006), Problemas Resueltos de Métodos Numéricos, Thomson, España
- Denidovich, B.P., Maron, I.A. (1988), Cálculo Numérico Fundamental, Paraninfo, Madrid
- Douglas, J., Burden, R. (2004), Métodos Numéricos, Thomson, España
- Martínez Salas, J. (1989), Métodos Matemáticos, Ed.el autor, Valladolid
- Ralston, A. (1985), Introducción al Análisis Numérico, Linusa, Mexico
- Scheid, F. (1990), Análisis Numérico, McGrawHill, Mexico
- Scheid, F. Constanzo, R.E.di (1991), Métodos Numéricos, McGrawHill
0 . Determinar el error del resultado de un cálculo a partir del error de los datos de los cuales partimos (PROPAGACIÓN DE ERRORES):
Actividad 0.1. Los datos experimentales con los que trabajamos vienen siempre dados con un cierto error. Si a partir de ellos realizamos cálculos, estos errores se propagan a los resultados. Así, si y=f(x), tendremos que ∆y=f(x+∆x)-f(x). Aun así, si el orden de magnitud del error es lo bastante inferior al orden de magnitud de los datos, podemos estimar el error por la diferencial, tomando así ∆y≈f ' (x)·∆x .
Problema 0.1: si y=x2, estimar el error de y en los siguiente casos:
a) x=2±1.
b) x=2'0±0'1.
c) x=2'00±0'01.
¿En qué casos la diferencial dará una buena estimación del error (expresando éste con una única cifra significativa, o 2 si la primera es 1)?.
Actividad 0.2.
Ejercicio 0.1: teniendo en cuenta que si z=f(x,y) entonces dz = fx'·∆x + fy'·∆y , obtener la expresión aproximada del error de z si z=x+y, z=x·y, z=x/y, z=x2, z=√x .
Actividad 0.3.
Problema 0.2: supongamos que una reacción viene regida por la ley de acción de mases v=k·[A]·[B]2, con k=0'254±0'001. Si se miden las concentraciones en equilibrio obteniéndose [A]=7'23±0'04 moles/l, [B]=9'58±0'12 moles/l, estimar el error de la velocidad de reacción en equilibrio.
1 . Inferir información sobre poblaciones a partir de una porción de las mismas (INTRODUCCIÓN A LA ESTADÍSTICA :
Actividad 1.1:
Debatir en
grupos pequeños el siguiente texto, escogiendo previamente un
portavoz
de cada grupo para exponer posteriormente las conclusiones y en su caso
las dudas suscitadas:
En numerosos problemas
prácticos estamos interesados en propiedades globales de
poblaciones ,
más que en
las propiedades particulares de cada uno de los individuos que las
composen.
Estas propiedades globales de las poblaciones (y entendemos por
población cualquier conjunto, cuyos elementos son
tratados de forma indiferenciada) son el
objeto
de la Estadística:
desde un punto de vista estadístico, lo que
interesa no
es qué individuos tienen una propiedad determinada,
sino
cuantos la tienen.
Ahora bien,
normalmente no tenemos acceso a las poblaciones en
su conjunto,
sino solamente a porciones de las mismas (a las cuales
denominamos muestras),
y nos interesa poder
inferir propiedades globales a partir del estudio de estas porciones.
Esta inferencia es el objetivo
central de la Estadística.
La inferencia
estadística es fundamental para la investigación
científica: habitualmente, se construyen teorías globales
sobre
poblaciones, las cuales se contrastan con estudios experimentales sobre
muestras de las mismas. Pero es importante
recalcar que
la inferencia estadística solamente permite llegar
a estimaciones, y no a afirmaciones concluyentes.
Por
todo esto,
podríamos decir que la Estadística, por su propia
naturaleza,
es una ciencia "democrática"
por su objeto (poblaciones globales, que pueden ser tanto de objetos
inanimados como de personas humanas) y "antidogmàtica"
por su método, que excluye certezas definitivas.
1.1. Aprender a obtener medidas de centralización y dispersión en una distribución estadística:
Objetivos:
- Comprender la noción de distribución estadística y su no dependencia de las propiedades específicos de individuos específicos.
- Aprender a comparar diferentes distribuciones estadísticas por el valor alrededor del cual se agrupan sus valores.
- Aprender a comparar diferentes distribuciones estadísticas por la dispersión de sus valores.
- Entender en qué medida varían las medidas de centralización y dispersión de una distribución estadística al sumar, restar, multiplicar o dividir sus valores por una cantidad fija.
- Aprender a calcular las medidas de centralización y dispersión de forma que se simplifiquen los cálculos y se eviten los errores de cancelación.
- Aprender a normalizar las distribuciones
estadísticas a fin de hacerlas comparables más
allá de sus
medidas
de centralización y dispersión.
Actividad 1.2. Una variable
aleatoria (X) sobre un
conjunto-población U es cualquier variable que puede
tener
distintos valores (x) para los distintos elementos-individuos de la
población
La distribución
estadística de estos valoras no tiene
en cuenta los
individuos concretos para los que esta variable tiene cada
valor,
sino cuántos la tienen, lo que denominamos frecuencia
f(x) de este valor en la población. Llamaremos parámetro
poblacional a cualquier cantidad que solamente dependa de las
frecuencias. Dos variables aleatorias serán
estadísticamente equivalentes
cuando tengan la misma distribución de frecuencias
Ejercicio 1.1:
tomar
una variable aleatoria sobre el alumnado asistente a la clase,
por ejemplo el hecho de llevar o no llevar gafas, y realizar un
experimento sencillo a fin de comprobar que el número de los
que llevan gafas es un parámetro poblacional.
Actividad 1.3.
Ejercicio 1.2:
representar gráficamente en diagramas de barras la
distribución
estadística de las frecuencias
del
número de calzado y de la edad en el alumnado asistente a clase.
Actividad 1.4.
Como medidas de centralidad
(valor
alrededor del cual se agrupan los valores de la variable
aleatoria) podemos tomar:
La moda:
aquel valor que
tenga la máxima frecuencia en
la población.
La mediana:
suponiendo que el
conjunto de valores de la variable aleatoria esté
ordenado,
será un valor que tenga tantos individuos con un valor
inferior
como con un valor superior.
La media
μ(X): suponiendo que
los
valores de la variable aleatoria sean números
reales, y que
el tamaño
(número de individuos n(U)) de la población sea
finito, viene
dada por
la suma de los valores Xi para
todos los individuos i de la población
dividida
por su tamaño, μ(X) = ∑ i
Xi
/ n(U) .
Teorema 1.1:
∑
x f(x) = n(U)
, μ(X) = ∑
x x·f(x) / n(U) .
Problema 1.1:
calcular
las diferentes medidas de centralización para las
distribuciones
estadísticas de la Actividad 1.3. ¿Cómo podemos
utilizar
las
frecuencias para simplificar los cálculos?
Actividad 1.5.
Para
justificar que el cálculo de la media es
una operación lineal, demostrar los siguientes teoremas:
Teorema 1.2:
si tenemos
dos variables aleatorias X, Y con valores
numéricos reales
sobre la misma población U,
μ(X+Y)=μ(X)+μ(Y) .
Teorema 1.3:
si tenemos
una variable aleatoria sumable X y un número real
constante c, μ(c·X)=c·μ(X) .
Actividad 1.6.
A partir de la linealidad
del cálculo de la media expresada en los dos
teoremas anteriores, y teniendo en cuenta que la media de una constante
es igual a la misma constante, demostrar
Teorema 1.4:
si tenemos
una variable aleatoria X con valores numéricos
reales y un
número real acR,
entonces μ(X)=a+μ(X-a) .
Teorema 1.5:
si tenemos
una variable aleatoria X con valores numéricos
reales y dos
números reales a,ccR,
y tomamos Y=(X-a)/c, entonces μ(X)=a+c·μ(Y) .
Los teoremas anteriores se pueden utilizar para simplificar el
cálculo de la media. Aplicarlo para la resolución
del
Problema 1.2:
medir la longitud
de la propia mano con una
precisión de 0'5
cm y calcular la media del conjunto del alumnado asistente a clase.
Actividad 1.7.
Como medidas
de dispersión
(para expresar el alejamiento entre sí de los valores de una
variable
aleatoria) podemos tomar:
Los cuartiles
primero y tercero:
suponiendo que el conjunto de valores de la variable
aleatoria
esté ordenado, los cuartiles serán tres valores que
dividan al conjunto de valores en cuatro subconjuntos de valores que
correspondan al mismo número de individuos; observamos que
el segundo cuartil coincidirá con la mediana. Si tenemos
definida una distancia en el conjunto de valores, podemos
medir la dispersión
como la distancia entre el primero y el
tercer cuartil.
La amplitud:
suponiendo que los
valores estén ordenados y tengamos definida una distancia
entre
ellos, será la distancia entre los valores
mínimo y máximo
en la población.
La desviación
media:
suponiendo que los valores de la variable aleatoria sean
números reales y que el tamaño de la población
sea finito,
será la media del valor absoluto de las
diferèncias
entre su
valor para cada individuo y la media de estos valores,
μ(|X-μ(X)|)
La varianza
σ2(X):
suponiendo que los valores de la variable aleatoria sean
números reales y que el
tamaño de la población sea finito,
será la media
del cuadrado de las diferencias entre su valor para cada
individuo y la media de estos valores, σ2(X)=μ((X-μ(X))2).
La desviación típica
σ(X): es la raíz cuadrada de la varianza.
Demostrar el
Teorema 1.6:
σ2(X)=μ(X2)-μ(X)2
(la variança es igual a la media
de los cuadrados menos el cuadrado de la media).
Este teorema proporciona una forma más cómoda
de calcular
la varianza.
Problema 1.3:
calcular
las diferentes medidas de dispersión para las distribuciones
estadísticas de la Actividad 1.3.
Problema 1.4:
calcular
la varianza de este conjunto de valores: (1000000'1
, 1000000'2
, 1000000'2, 1000000'3).
Actividad 1.8.
Cómo habremos
visto al intentar resolver el Problema 1.4, si la media de una
distribución estadística es mucho más
grande
que su amplitud,
entonces la media del cuadrado y el cuadrado de la media tendrán
muchas cifras significativas coincidentes, que pueden incluso
superar la precisión de nuestros instrumentos de cálculo;
en este caso, obtendríamos erróneamente cero como su
diferencia, produciéndose así un "error de
cancelación". A fin de poder evitarlo utilizando las
propiedades de la varianza, demostrar el
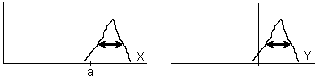 Teorema 1.7:
si tenemos
una variable aleatoria X con valores numéricos
reales y un
número real acR,
y tomamos Y=X-a, entonces σ2(Y)=σ2(X)
, es decir, la varianza es invariant
ante
traslaciones, como se puede entender fácilmente observando la
figura
adjunta.
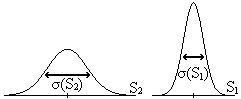
Teorema 1.7:
si tenemos
una variable aleatoria X con valores numéricos
reales y un
número real acR,
y tomamos Y=X-a, entonces σ2(Y)=σ2(X)
, es decir, la varianza es invariant
ante
traslaciones, como se puede entender fácilmente observando la
figura
adjunta.
Por lo tanto, podremos evitar el error de cancelación restando a
todos
los
valores una cantidad fija
próxima a su
valor mínimo. Aplicarlo a la resolución del
Problema
1.4.
Actividad 1.9.
Demostrar el
Teorema 1.8:
si tenemos
una variable aleatoria X con valores numéricos
reales y dos
números reales a,ccR+,
y tomamos Y=(X-a)/c, entonces
σ(X)=c·σ(Y) .
Aplicarlo por simplificar la resolución del
Problema 1.5:
calcular
la varianza de la distribución
estadística del
Problema 1.2.
Actividad 1.10.
Para comparar
la forma de distribuciones estadísticas con diferentes
medias y varianzas
podemos transformarlas en otras distribuciones
estadísticas con medias y varianzas coincidentes. Llamaremos
así normalización
de una variable aleatoria X al resultado de restarle su
media y dividir la diferencia
por su desviación
típica,
N(X)=(X-μ(X))/σ(X) . Demostrar el
Teorema 1.9:
μ(N(X))=0 y σ(N(X))=1.
Ejercicio 1.3:
Representar gráficamente en la misma figura la
normalización
de las distribuciones estadísticas
de la Actividad
1.3.
1.2. Estudiar casos típicos de distribuciones estadísticas de probabilidades
Objetivos:
- Trabajar las distribuciones estadísticas a partir de las frecuencias relativas (probabilidades).
- Averiguar la distribución probabilística del número de ocurrencias de un suceso entre un número de ocasiones independientes. (distribución binomial).
- Aproximar la distribución probabilística del número de ocurrencias de un suceso raro conociendo el número medio de ocurrencias entre un número grande de ocasiones independientes (distribución de Poisson).
- Introducir la distribución de densidad probabilística de una variable aleatoria que varía de forma continua.
- Estudiar la distribución de densidad probabilística de la media de un gran número de variables aleatorias equivalentes independientes (distribución normal).
Demostrar los siguientes teoremas:
Teorema 1.10: ∑ x p(x) = 1 (llamaremos distribución probabilística a cualquier aplicación p:V→R++{0} que cumpla esta propiedad, siendo V un conjunto numerable de valores .
Teorema 1.11: μ(X) = ∑ x x·p(x) (utilizaremos esta expresión para definir la media de cualquier distribución probabilísitica con independencia del tamaño finito o infinito de la población .
Ejercicio 1.4: representar gráficamente en diagramas de tarta las distribuciones probabilísticas de las variables aleatorias de la actividad 1.3.
Actividad 1.12. Si tenemos un conjunto A de valores de una variable aleatoria, su probabilidad vendrá definida por
p(A) = ∑ xcA p(x) . Demostrar el
Teorema 1.12: Si A y B son dos conjuntos disjuntos de valores de una variable aleatoria, p(A+B) = p(A) + p(B) .
Actividad 1.13. Diremos que dos variables X, Y son independientes si para cualquier par (x, y) de valores respectivos de las mismas se cumple p(x,y)=p(x)·p(y) .
Problema 1.6: estudiar si las variables aleatorias de la Actividad 1.3 son independientes.
Actividad 1.14. Teniendo en cuenta el
Teorema -1.1: el número de maneras en que podemos escoger m elementos entre n es
| ﴾ |
n m |
﴿ = |
n(n-1)(n-2)...(n-(m-1))
m! |
= |
n!
m!(n-m)! |
(combinaciones
de n sobre m) |
Teorema 1.13: Si tenemos n variables-ocasiones independientes con un determinado valor-suceso con la misma probabilidad p, la probabilidad de no ocurrencia de cada suceso será q=1-p y la probabilidad de que el número de ocurrencias del suceso sea exactamente m será
| PB(m)
= ﴾ |
n m |
﴿ pm
qn-m (distribución
binomial B(p,n)) |
Problema 1.7: calcular la probabilidad de obtener exactamente 3 ases en 5 lanzamientos de un dado.
Actividad 1.15. Teniendo en cuenta el
| Teorema -1.2:
(a+b)n
= |
n ∑ . m=0. |
﴾ | n m |
﴿ am
bn-m (binomio
de Newton) |
| Teorema 1.14: |
n ∑ . m=0. |
PB(m) = 1. |
Actividad 1.16. Teniendo en cuenta el
Teorema -1.3: 0!=1 , m!=m·(m-1)!
demostrar los
| Teorema 1.15:
para
todo m=1...n, ﴾ |
n m |
﴿·m = n·﴾ | n-1 m-1 |
﴿ |
Actividad 1.17. Demostrar los
| Teorema 1.17:
para
todo m=2...n, m·﴾ |
n-1 m-1 |
﴿ = (n-1)·﴾ | n-2 m-2 |
﴿ + ﴾ | n-1 m-1 |
﴿ |
Actividad 1.18.
Problema 1.8: obtener la media y la desviación típica del número de ases al lanzar 30 veces un dado.
Actividad 1.19. Si p es muy pequeño, para obtener una media μ apreciable de ocurrencias de un suceso necesitaremos un número n muy grande de ocasiones. Pero los factoriales n!, y por lo tanto la distribución binomial, son difíciles de calcular si n es grande. En este caso, habremos de utilizar una aproximación. A tal efecto, y teniendo en cuenta que e = lim u→∞ (1+1/u)u, y por lo tanto
Teorema -1.4: lim n→∞ (1-μ/n)n = e-μ
demostrar el
Teorema 1.19: si p=μ/n, PΠ(m) = lim n→∞ PB(m) = e-μ·μm/m! (distribución de Poisson Π(μ)).
La distribución de Poisson es una buena aproximación a la binomial si n>50, p<0'1 y μ=np<5 .
Actividad 1.20. Teniendo en cuenta el
| Teorema -1.5: eμ = | ∞ ∑ m=0. |
μm/m! (desarrollo en serie de Taylor del exponencial) |
| Teorema 1.20: | ∞ ∑ m=0. |
PΠ(m) = 1. |
Teorema 1.22: σ(Π(μ))2 = μ
Actividad 1.21.
Problema 1.9: suponiendo que la probabilidad de obtener un preparado químico por un determinado procedimiento sea de 0'01, ¿cual será el número medio de éxitos y la probabilidad de tener al menos un éxito en 200 pruebas? Obtener el valor exacto por la distribución binomial y el valor aproximado por la distribución de Poisson y compararlos.
Actividad 1.22. Si tenemos una variable aleatoria que varía de forma continua en R, habremos de definir un conjunto de intervalos de la misma para determinar las frecuencias o probabilidades de los valores en cada intervalo,
 como
hicimos en el Problema 1.2 con la longitud de la mano.
Pero
podemos definir también una distribución
de densidad probabilística
mediante una
función p:R→R++{0} que
cumpla
como
hicimos en el Problema 1.2 con la longitud de la mano.
Pero
podemos definir también una distribución
de densidad probabilística
mediante una
función p:R→R++{0} que
cumpla ∫ p(x) dx = 1 .
En este caso, la probabilidad de un intervalo [a,b[ vendrá dada por
p([a,b]) = ∫ab p(x) dx
Naturalmente, si hacemos una partición de R en un conjunto de intervalos disjuntos, la suma de sus probabilidades valdrá 1. A partir del
Teorema -1.6: para toda función integrable f y todo intervalo [a,b[ de R, existe ξc[a,b[ tal que
∫ab x·p(x) dx = ξ·∫ab p(x) dx
demostrar el
Teorema 1.23: si tenemos una distribución p de densidad probabilísitca, partimos R en intervalos disjuntos [z-ε,z+ε[ tomando z como valor del intervalo, y definimos la media de la distribución de densidad probabilística como el límite de la media de la correspondiente distribución probabilística cuando ε tienda a cero será μ(X) = ∫ x·p(x) dx .
Teorema 1.24: definiendo la varianza de una distribución p de densidad probabilística como μ((X-μ(X))2), será
σ2(X) = ∫ x2·p(x) dx - μ(X)2 .
Actividad 1.23. Definimos la distribución normal N(α,β) por PN(x) = e-(x-α)2/(2β2)/(β(2π)1/2) para todo xcR .
Teniendo en cuenta el
Teorema -1.7: ∫-∞∞ e-u2du = √π , ∫-∞∞ ue-u2du = 0 , ∫-∞∞ u2e-u2du = (√π)/2.
demostrar los
Teorema 1.25: ∫-∞∞ PN(x) dx = 1 (y por lo tanto se trata de una distribución de densidad probabilística)
Teorema 1.26: μ(N(α,β)) = α
Teorema 1.27: σ(N(α,β)) = β
Escribiremos por lo tanto N(μ,σ) y PN(x) = e-(x-μ)2/(2σ2)/(σ(2π)1/2) .
Actividad 1.24. Definimos la distribución normal tipificada como N(0,1), de modo que PN(y) = e-y2/2/(2π)1/2 .
Trabajaremos con la tabla de la distribución normal tipificada. A partir de ésta podemos obtener fácilmente los valores de otra distribución normal mediante la normalización de su variable x, de forma que y=(x-μ)/σ , y teniendo en cuenta que PN(y)=σ·PN(x) .
Problema 1.10. Utilizando la tabla de la distribución normal tipificada, obtener la densidad probabilística de una distribución normal con μ=5, σ=2 para x=7'4.
Actividad 1.25. La importancia de la distribución normal para el estudio de la Estadística resulta justificada por el siguiente
Teorema 1.28: si tenemos una sucesión de variables aleatorias independientes Xi con la misma media y desviación típica, μ(Xi )=μ, σ(Xi )=σ, y definimos Zn = ∑i=1 n Xi/n, entonces la distribución estadística de lim n→∞ N(Zn) es la distribución normal tipificada N(0,1) (Teorema central del límite).
De acuerdo con este teorema, la distribución normal dará una buena aproximación de la media de un gran número de variables aleatorias equivalentes independientes, y podremos utilizarla cuando trabajemos con grandes cantidades de datos. En particular, se cumple el
Teorema 1.29: lim n→∞ PB(p,n)(m) / PN(np,√(np(1-p)))(m) = 1 (teorema de De Moivre; para cada valor de m, la sucesión de valores de n será n=m, m+1, m+2...)
La distribución normal es una buena aproximación a la binomial si n·p>5 y n·q>5 .
Problema 1.11: comparar las distribuciones normal, binomial y de Poisson en los siguientes casos:
a) Aplicar la distribución normal para intentar aproximar la solución del Problema 1.9. ¿Da una buena aproximación?
b) Suponiendo que la probabilidad de obtener un preparado químico por un determinado procedimiento sea de 0'5, ¿cual será la probabilidad de tener únicamente un fracaso en 10 pruebas? Obtener el valor exacto por la distribución binomial e intentar aproximarlo por las distribuciones normal y de Poisson. ¿Cuál da una mejor aproximación?
Trabajo 1 (para su realización en equipo):
Estudiar las condiciones de aproximación de las distribuciones normal y de Poisson a la distribución binomial, utilizando diferentes fuentes bibiogràfiques (por ejemplo
http://www.gestiopolis.com/recursos/experto/catsexp/pagans/eco/44/distripoisson.htm
http://www.suagm.edu/paginas/japaricio/384/clase11.pdf
http://www.jstor.org/sici?sici=0003-4851(196009)31%3A3%3C737%3ATPATTP%3E2.0.CO%3B2-Q&cookieSet=1
http://leonsotelo.blogspot.com/2007/06/aproximacion-normal-binomial-poiss0n.html
http://www.mitecnologico.com/Main/AproximacionDeBinomialPorDePoisson )
Estudiar y comparar en particular el caso n=30, p=1/6. Obtener una tabla de las tres distribuciones (para valores enteros no negativos) y representarlas gráficamente en la misma figura.
1.3. Hacer
estimaciones sobre una población a partir de una muestra:
Objetivos:
- Estudiar las propiedades de las distribuciones de las muestras de una población.
- Identificar los estadísticos-parámetros de una muestra que mejor permiten estimar los parámetros de la población
- Construir intervalos que contengan con una cierta probabilidad el valor de un parámetro poblacional.
- Determinar la probabilidad de equivocarnos al rechazar una hipótesis a partir de unos datos experimentales.
- Trabajar con las distribuciones adecuadas según las muestras utilizadas y los parámetros a estimar.
- Contrastar hipótesis probabilísticas.
Actividad 1.26.
Una muestra sin
reemplazo
es cualquier subconjunto de una población (un
ejemplo
típico es una mano de cartas de una baraja). Una muestra
con reemplazo
se obtiene escogiendo sucesivamente un determinado
número
de elementos de la población sin quitarlos de la misma, de forma
que
pueden repetirse (un ejemplo típico es
el resultado de tiradas sucesivas de un dado). Llamaremos estadístico
a cualquier
parámetro poblacional restringido a una muestra. Para
distinguirlo del correspondiente parámetro sobre
la población, utilizaremos una nomenclatura diferente;
así,
designaremos la media de una variable aleatoria X en una
muestra
por  , y
su
desviación típica por s(X).
, y
su
desviación típica por s(X).
Trabajaremos con distribuciones en 3 ámbitos: en
la población, en una muestra y en el conjunto de todas las
muestras.
Naturalmente, para poder hacer estimaciones sobre una población
a
partir de una
muestra necesitaremos saber cómo se distribuyen los valores
del estadístico correspondiente en el conjunto de todas las
muestras
de la población de un determinado tipo (con o sin
reemplazo) y de un determinado tamaño; a esta
distribución la llamaremos distribución
muestral. Las principales propiedades de ésta se resumen
en
la siguiente tabla, dónde indicamos por n(U) el tamaño
de la población
y por n el tamaño de la muestra:
| parámetro poblacional Ω |
estadístico S |
distribución muestral sin
reemplazo μ(S), σ(S) |
distribución muestral con
reemplazo μ(S), σ(S) |
| μ(X) |
 |
μ( )
= μ(X) )
= μ(X) |
|
σ( )2
= σ(X)2(n(U)-n)/(n·(n(U)-1)) )2
= σ(X)2(n(U)-n)/(n·(n(U)-1)) |
σ( )2
= σ(X)2/n )2
= σ(X)2/n |
||
| σ(X) |
s(X) |
μ(s(X)2)
= σ(X)2·(n-1)/n σ(s(X))2 ≈ σ(X)2/(2n) si n≥100. |
|
Problema 1.12: Obtener la varianza de la distribución muestral de medias y la media de la distribución muestral de varianzas con muestras formadas por la repetición 3 veces del lanzamiento de 5 dados anotando en cada lanzamiento el número de ases obtenidos (suponiendo que los dados no están cargados). Dividir la clase en grupos de 3 de modo que cada miembro haga un lanzamiento de 5 dados, calculando en cada grupo la media y la varianza de la muestra obtenida. Calcular la varianza de las medias y la media de las varianzas obtenidas por toda la clase y compararlas con los previos resultados teóricos.
Actividad 1.27.
Para
estimar correctamente un parámetro poblacional Ω
necesitaremos un
estadístico S que sea un
estimador
insesgado del mismo, de forma que μ(S) =
Ω. En caso de que no lo sea pero conozcamos el sesgo que se
produce, de forma que μ(S) = f(Ω), siendo f una
función lineal,
podemos definir un estimador corregido 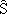 = f -1(S)
tal que μ(
= f -1(S)
tal que μ(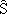 )
= Ω .
)
= Ω .
Ejercicio 1.5:
analizar si la media  y la varianza s2
son o no estimadores insesgados de los correspondientes
parámetros poblacionales μ(X) y σ(X). En caso de que
alguno no
lo sea, obtener el correspondiente estadístico corregido y
comprobar
que es un estimador insesgado.
y la varianza s2
son o no estimadores insesgados de los correspondientes
parámetros poblacionales μ(X) y σ(X). En caso de que
alguno no
lo sea, obtener el correspondiente estadístico corregido y
comprobar
que es un estimador insesgado.
 Actividad 1.28. Si tenemos dos
estimadores
insesgados S1 y S2,
diremos que S1
es más eficiente
que S2 si y solamente
si σ(S1)<σ(S2).
Actividad 1.28. Si tenemos dos
estimadores
insesgados S1 y S2,
diremos que S1
es más eficiente
que S2 si y solamente
si σ(S1)<σ(S2).
Ejercicio 1.6:
queremos
estimar la media μ de una población a partir de las
medias
 1,
1,
 2
de dos muestras de tamaño respectivo n1,
n2 tales que n1<n2.
Qué estimador será más eficiente? Demostrarlo.
2
de dos muestras de tamaño respectivo n1,
n2 tales que n1<n2.
Qué estimador será más eficiente? Demostrarlo.
 Actividad
1.29. Diremos que [Ω1,Ω2]
es un intervalo de confianza
del 100α% para un parámetro poblacional
Ω si la probabilidad de que Ω esté dentro de este intervalo es
igual a .
α. Para
determinarlo necesitaremos conocer la distribución
muestral de alguna función f(S,Ω), siendo S
el estadístico
de una muestra que utilizamos para estimar Ω. En general,
buscaremos en
esta distribución muestral de densidad
probabilística
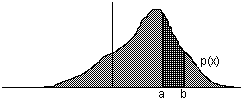
dos "picos" de probabilidad p, de forma que el área entre los
dos
"picos" sea α, tal y como se indica en la figura adjunta.
Observamos que, comoquiera que
el área bajo la curva es 1, se
ha de cumplir 2p+α=1
. Las abcises correspondientes a una determinada área se
denominan coeficientes
críticos. Hay que
examinar con cuidado la configuración de la tabla de la
distribución
y las gráficas que la acompañan para
determinar a qué área se refiere cada coeficiente
crítico
(parte de la izquierda, interior, exterior...) y qué
son por tanto los coeficientes tales
que xp≤f(S,Ω)≤x1-p
nos da un intervalo de confianza para
Ω del 100α% .
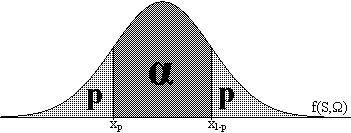
Actividad
1.29. Diremos que [Ω1,Ω2]
es un intervalo de confianza
del 100α% para un parámetro poblacional
Ω si la probabilidad de que Ω esté dentro de este intervalo es
igual a .
α. Para
determinarlo necesitaremos conocer la distribución
muestral de alguna función f(S,Ω), siendo S
el estadístico
de una muestra que utilizamos para estimar Ω. En general,
buscaremos en
esta distribución muestral de densidad
probabilística
dos "picos" de probabilidad p, de forma que el área entre los
dos
"picos" sea α, tal y como se indica en la figura adjunta.
Observamos que, comoquiera que
el área bajo la curva es 1, se
ha de cumplir 2p+α=1
. Las abcises correspondientes a una determinada área se
denominan coeficientes
críticos. Hay que
examinar con cuidado la configuración de la tabla de la
distribución
y las gráficas que la acompañan para
determinar a qué área se refiere cada coeficiente
crítico
(parte de la izquierda, interior, exterior...) y qué
son por tanto los coeficientes tales
que xp≤f(S,Ω)≤x1-p
nos da un intervalo de confianza para
Ω del 100α% .
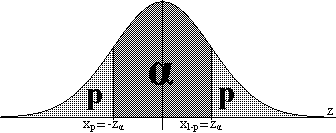 Ejercicio 1.7: si
las
muestras son grandes (n≥30) y el parámetro
poblacional
es la media poblacional, entonces tomando la normalización
de la media de la muestra,
Ejercicio 1.7: si
las
muestras son grandes (n≥30) y el parámetro
poblacional
es la media poblacional, entonces tomando la normalización
de la media de la muestra,
z = f( ,μ)
= (
,μ)
= ( -μ)/σ(
-μ)/σ( ),
se
distribuirá aproximadamente de acuerdo con
la distribución
normal tipificada. Para obtener el intervalo de
confianza
habremos de calcular
primero la media y la desviación típica
de la muestra,
),
se
distribuirá aproximadamente de acuerdo con
la distribución
normal tipificada. Para obtener el intervalo de
confianza
habremos de calcular
primero la media y la desviación típica
de la muestra,  ,
s; a continuación calcular la desviación
típica
corregida
,
s; a continuación calcular la desviación
típica
corregida  , utilizarla como estimador insesgado de la
desviación
típica poblacional σ, y a partir del
valor
estimado de ésta obtener la desviación típica de
las
medias en la distribución muestral, σ(
, utilizarla como estimador insesgado de la
desviación
típica poblacional σ, y a partir del
valor
estimado de ésta obtener la desviación típica de
las
medias en la distribución muestral, σ( ).
Utilizando
la tabla
de la distribución normal tipificada (inversa)
para
obtener el
coeficiente crítico zα
tal que la probabilidad
de |z|≤zα
sea α (recordemos que la distribución
normal tipificada es
simétrica) podremos averiguar el intervalo de confianza
para μ. Obtener las
fórmulas correspondientes.
).
Utilizando
la tabla
de la distribución normal tipificada (inversa)
para
obtener el
coeficiente crítico zα
tal que la probabilidad
de |z|≤zα
sea α (recordemos que la distribución
normal tipificada es
simétrica) podremos averiguar el intervalo de confianza
para μ. Obtener las
fórmulas correspondientes.
Problema 1.13:
aplicarlo a la obtención de un intervalo de confianza
del
80% para el número mediano de ases resultantes de lanzar
30 veces un dado a partir de los resultados
experimentales
obtenidos por todos los alumnos de la clase (en un número no
inferior a 30).
Actividad 1.30.
Si por consideraciones teóricas formulamos la hipótesis
de un valor para un parámetro
poblacional Ω, y a partir de una muestra experimental obtenemos
un intervalo de confianza del 100α% para este
parámetro poblacional, si el valor
teórico de éste está fuera de este intervalo,
es decir
f(S,Ω) [xp,x1-p],
pueden
haber dos explicaciones: la primera es que la teoría y por lo
tanto
la hipótesis esté equivocada; la segunda es
que la muestra sea "anómala", de modo que siendo correcta
la teoría el parámetro poblacional Ω esté fuera
del intervalo de confianza del 100α%: la probabilidad
de esto
es β=1-α. Diremos así que
la muestra nos permite rechazar la hipótesis con un nivel de significación
de β (que será por lo tanto la probabilidad de que nos
equivoquemos al rechazar la hipótesis). Naturalmente,
solamente podremos rechazar hipótesis con niveles de
significación
iguales o menores a 0'5, y cuanto menor sea
el nivel de significación el rechazo de la hipótesis
tendrá más fuerza.
[xp,x1-p],
pueden
haber dos explicaciones: la primera es que la teoría y por lo
tanto
la hipótesis esté equivocada; la segunda es
que la muestra sea "anómala", de modo que siendo correcta
la teoría el parámetro poblacional Ω esté fuera
del intervalo de confianza del 100α%: la probabilidad
de esto
es β=1-α. Diremos así que
la muestra nos permite rechazar la hipótesis con un nivel de significación
de β (que será por lo tanto la probabilidad de que nos
equivoquemos al rechazar la hipótesis). Naturalmente,
solamente podremos rechazar hipótesis con niveles de
significación
iguales o menores a 0'5, y cuanto menor sea
el nivel de significación el rechazo de la hipótesis
tendrá más fuerza.
Problema 1.14:
¿con qué nivel de significación podríamos
en su
caso
rechazar la hipótesis de que el dado del Problema 1.13 no
está cargado (es decir, que todas las caras del
dado tienen la misma probabilidad de salir)?
Actividad 1.31.
Si las
muestras son pequeñas, su distribución no
se aproxima
a la normal. Pero si una variable aleatoria X
tiene
una distribución normal en una población infinita,
la distribución
del estadístico
t = f( ,μ)
= (
,μ)
= ( -μ(X))/σ(
-μ(X))/σ( )
de las
muestras de tamaño n es Yν(t)=Yν(0)·(1+t2/ν)-(ν+1)/2
con ν=n-1, que se denomina distribución
t de "Student" con
ν grados de libertad.
Yν(0) se escoge de modo que ∫-∞+∞
Yν(t)dt=1 .
)
de las
muestras de tamaño n es Yν(t)=Yν(0)·(1+t2/ν)-(ν+1)/2
con ν=n-1, que se denomina distribución
t de "Student" con
ν grados de libertad.
Yν(0) se escoge de modo que ∫-∞+∞
Yν(t)dt=1 .
Teniendo en cuenta que e = lim
u→∞ (1+1/u), demostrar el
Teorema 1.30:
lim
ν→∞ Yν(t)
= PN(0,1)(t)
(es decir, la distribución t
de "Student" se aproxima
a la distribución
normal tipificada cuando el número de grados
de libertad
se hace
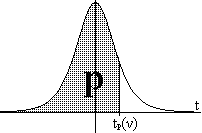
muy grande); ¿cuanto valdrá Y∞(0)?
 Actividad 1.32.
Utilizaremos
la tabla
de la distribución t
de "Student"
(inversa) para
determinar el
coeficiente crítico tp(ν)
correspondiente al
intervalo de confianza del 100α% de la media
poblacional μ a partir de la media
Actividad 1.32.
Utilizaremos
la tabla
de la distribución t
de "Student"
(inversa) para
determinar el
coeficiente crítico tp(ν)
correspondiente al
intervalo de confianza del 100α% de la media
poblacional μ a partir de la media  y la
desviación
típica s(X) de una muestra de tamaño
n, con las fórmulas obtenidas en
el Ejercicio
1.7.
y la
desviación
típica s(X) de una muestra de tamaño
n, con las fórmulas obtenidas en
el Ejercicio
1.7.
Problema 1.15:
obtener
un intervalo de confianza del 90% para la media de una
variable
aleatoria en una población infinita con
distribución
normal a partir de la muestra
(302'23, 302'21, 302'23, 302'22, 302'25).
Actividad 1.33.
Problema 1.16:
formando
grupos de 3 a 5 estudiantes, cada estudiante en cada grupo
deberá
lanzar 30 veces un dado y anotar el número
de ases
obtenidos; hacer estimaciones alrededor de cada dado a partir de la
muestra
dada por los resultados obtenidos por cada grupo.
 Actividad 1.34. Si una
variable aleatoria X tiene una
distribución normal en
una población infinita, la distribución del
estadístico
Actividad 1.34. Si una
variable aleatoria X tiene una
distribución normal en
una población infinita, la distribución del
estadístico
χ2 =
f(s,σ) = n·s(X)2/σ(X)2
de las muestras de tamaño n entre 0 y ∞
es Vν(χ2)=Kν·(χ2)(ν-2)/2·e-χ2/2
con ν=n-1, que se denomina distribución Ji-cuadrado
con ν grados de libertad. Kν
se escoge de modo que
∫0∞ Vν(χ2)=1
. Utilizaremos la tabla
de
la distribución Ji-cuadrado (inversa) para
determinar los
coeficientes críticos χ2p(ν)
correspondientes al
intervalo de confianza del 100α% de la desviación
típica poblacional σ a partir de la desviación
típica s(X) de una muestra
de tamaño
n, de modo que χ2p(ν)
≤ χ2
≤ χ21-p(ν)
. Obtener la expresión para el intervalo de confianza
de la desviación
típica poblacional σ(X).
Observemos que la desviación
típica corregida  (X)
de la muestra
ha de estar necesariamente dentro de este intervalo, comoquiera que
es un estimador insesgado de la desviación
típica poblacional.
(X)
de la muestra
ha de estar necesariamente dentro de este intervalo, comoquiera que
es un estimador insesgado de la desviación
típica poblacional.
Problema 1.17:
obtener
un intervalo de confianza del 90% para la desviación
típica de una variable
aleatoria en una población infinita con
distribución
normal a partir de la muestra (302'23, 302'21, 302'23, 302'22, 302'25);
comprobar que la desviación típica corregida de la
muestra
está dentro de este intervalo.
Actividad 1.35:
Si tenemos un
conjunto de k sucesos mutuament excluyentes Ei
a los que suponemos una probabilidad p(Ei)
para
i=1...k, en n ocasiones la frecuencia esperada de cada uno de ellos
será respectivamente ei=n·p(Ei),
correspondiente a la media obtenida en el Teorema 1.16. Si en una
muestra de estas n ocasiones las frecuencias
observadas
son respectivamente oi, siendo n≥30 y
cumpliéndose ei≥5
para todos los sucesos, entonces el estadístico χ2
= ∑i=1 k (oi-ei)2/ei
se
distribuirá aproximadamente de acuerdo con
la distribución Ji-cuadrado con ν=k-1 grados de libertad.
Si para algún
suceso fuera ei<5
habríamos de agregar sucesos hasta conseguir que se cumpla la
condición.
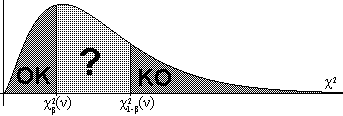 Podemos utilizar
este
estadístico para estimar la concordancia entre la
hipótesis
probabilística y los resultados
experimentales
obtenidos en la muestra. Naturalmente, cuanto menor sea χ2
habrá una mayor concordancia: diremos que hay buena concordancia
entre la muestra
y la hipótesis probabilística (y por lo tanto
aceptamos ésta) con un nivel de significación
de β si χ2<χ2β(ν);
por el contrario, si χ21-β(ν)<χ2
podremos rechazar
la hipótesis
probabilística con un nivel de significación
de β (que será de nuevo la probabilidad
de equivocarnos al rechazarla, es decir la probabilidad de que
la hipótesis sea correcta pero hayamos encontrado una
muestra
entre el 100β% de las muestras más desviadas de las
frecuencias medias esperadas); finalmente si
χ2β(ν)≤χ2≤χ21-β(ν)
diremos que los resultados experimentales no son decisivos con este
nivel
de significación para aceptar o rechazar la hipótesis
probabilística. Observamos que una hipótesis
probabilística puede ser aceptada (o rechazada) con un nivel
de significación
"débil" y los resultados no ser decisivos con un
nivel de significación más fuerte. Lo que no puede
pasar
es que con un nivel de significación aceptemos una
hipótesis y con otro nivel de significación la
rechacemos.
Naturalmente, el nivel de significación más débil
que
podemos utilizar es el de β=0'5: si χ2<χ20'5(ν)
tendremos tendencia a aceptar la hipótesis con un
nivel
de significación mayor o menor, y si χ2>χ20'5(ν)
tendremos tendencia a rechazarla.
Podemos utilizar
este
estadístico para estimar la concordancia entre la
hipótesis
probabilística y los resultados
experimentales
obtenidos en la muestra. Naturalmente, cuanto menor sea χ2
habrá una mayor concordancia: diremos que hay buena concordancia
entre la muestra
y la hipótesis probabilística (y por lo tanto
aceptamos ésta) con un nivel de significación
de β si χ2<χ2β(ν);
por el contrario, si χ21-β(ν)<χ2
podremos rechazar
la hipótesis
probabilística con un nivel de significación
de β (que será de nuevo la probabilidad
de equivocarnos al rechazarla, es decir la probabilidad de que
la hipótesis sea correcta pero hayamos encontrado una
muestra
entre el 100β% de las muestras más desviadas de las
frecuencias medias esperadas); finalmente si
χ2β(ν)≤χ2≤χ21-β(ν)
diremos que los resultados experimentales no son decisivos con este
nivel
de significación para aceptar o rechazar la hipótesis
probabilística. Observamos que una hipótesis
probabilística puede ser aceptada (o rechazada) con un nivel
de significación
"débil" y los resultados no ser decisivos con un
nivel de significación más fuerte. Lo que no puede
pasar
es que con un nivel de significación aceptemos una
hipótesis y con otro nivel de significación la
rechacemos.
Naturalmente, el nivel de significación más débil
que
podemos utilizar es el de β=0'5: si χ2<χ20'5(ν)
tendremos tendencia a aceptar la hipótesis con un
nivel
de significación mayor o menor, y si χ2>χ20'5(ν)
tendremos tendencia a rechazarla.
Problema 1.18:
contrastar la hipótesis de que un dado no está
cargado
(que todas las caras tienen la misma probabilidad de salir)
lanzándolo 30 veces y anotando el número de veces
que
sale cada cara.
Trabajo 2
(para su
realización en equipo):
En 100000 tiradas de 5 dados se obtiene 10 repóqueres, 300
póqueres, 3342 tríos, 16030 parejas y 40198 simples ases.
¿Se
podría acusar que los dados están trucados? ¿Con
qué nivel de significación
en tal caso?
1.4. Obtener una
recta
que tenga la menor
desviación posible de un
conjunto de puntos:
Objetivos:
- Obtener la recta que minimice la suma de las desviaciones cuadráticas de las ordenadas de un conjunto de puntos.
- Obtener la recta que minimice la suma de las desviaciones cuadráticas de las abcisas de un conjunto de puntos.
- Valorar el grado de ajuste de la recta de regresión al correspondiente conjunto de puntos.
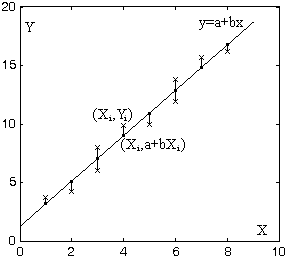 Actividad
1.36. Si tenemos un conjunto de puntos {Xi,
Yi}i=1...n, diremos que
y=a+bx es la recta
de regresión de Y
sobre X si y sólo si
Actividad
1.36. Si tenemos un conjunto de puntos {Xi,
Yi}i=1...n, diremos que
y=a+bx es la recta
de regresión de Y
sobre X si y sólo si ∑i=1 n (Yi -(a+bXi ))2 es mínimo.
Teniendo la cuenta el
Teorema -1.8: si una función derivable f(x,y) tiene un mínimo en (a,b), entonces fx'(a,b)=0 y fy'(a,b)=0.
demostrar
Teorema 1.31: si y=a+bx es la recta de regresión de Y sobre X, entonces a+b·μ(X)=μ(Y), a·μ(X)+b·μ(X2)=μ(XY).
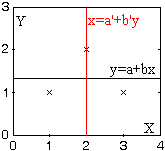
Teorema 1.32: si y=a+bx es la recta de regresión de Y sobre X, entonces b=cXY/σ(X)2, a=μ(Y)-b·μ(X), dónde cXY=μ(XY)-μ(X)·μ(Y) (covarianza de X y Y).
Actividad 1.37. Teniendo en cuenta el
Teorema -1.9: si para una función f(x,y) derivable hasta segundo orden se cumple fx'(a,b)=0 , fy'(a,b)=0, fxx"(a,b)>0 , fxy"(a,b)2<fxx"(a,b)·fyy"(a,b), entonces f(x,y) tiene un mínimo en (a,b)
demostrar el
Teorema 1.33: si σ(X)2>0 , b=cXY/σ(X)2, entonces y-μ(Y)=b·(x-μ(X)) es la recta de regresión de Y sobre X.
Observemos que el "centro de masas" (μ(X),μ(Y)) pertenece siempre a la recta de regresión.
Problema 1.19: obtener la recta de regresión del número de calzado sobre la edad en el alumnado asistente a clase; valorarla.
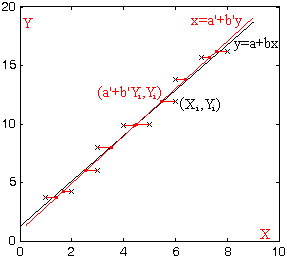 Actividad
1.38. Intercambiando la X y la Y obtenemos el
Actividad
1.38. Intercambiando la X y la Y obtenemos elTeorema 1.34: si σ(Y)2>0 , b'=cXY/σ(Y)2, entonces x-μ(X)=b·(y-μ(Y)) es la recta de regresión de X sobre Y.
Si σ(X)2>0 y σ(Y)2>0 , ambas rectas de regresión pasarán por el "centro de masas" (μ(X),μ(Y)), y definimos el coeficiente de correlación de X y Y por
ρXY = cXY/(σ(X)σ(Y)) .
Demostrar
Teorema 1.35: las rectas de regresión de Y sobre X y de X sobre Y coinciden si y sólo si ρXY = ±1 .
Teorema 1.36: si ρXY = 0, entonces las rectas de regresión son y=μ(Y) , x=μ(X) (perpendiculares).
Actividad 1.39. Diremos que dos variables aleatorias X, Y no tienen correlación lineal si y sólo si ρXY=0; esta condición es equivalente a la de cXY=0 con σ(X)>0 y σ(Y)>0.
Demostrar el
Teorema 1.36: si dos variables aleatorias son independientes, no tienen correlación lineal.
¿La recíproca es cierta? Comprobarlo en el siguiente
| Problema 1.20:
estudiar la correlación
lineal en el caso |
|
¿X e Y son independientes? |
Actividad 1.40. Demostrar
Teorema 1.37: σ(X±Y)2 = σ(X)2 + σ(Y)2 ± 2·cXY .
Teorema 1.38: si X,Y son independientes o simplemente no tienen correlación lineal, entonces σ(X±Y)2 = σ(X)2 + σ(Y)2 .
Actividad 1.41. Demostrar, utilizando el Teorema 1.37,
Teorema 1.39: Si y=a+bx es la recta de regresión de Y sobre X, entonces σ(Y-bX)2 = σ(Y)2(1-ρXY2) .
Teorema 1.40: -1 ≤ ρXY ≤ 1 .
Si ρXY>0 diremos que X,Y tienen correlación lineal positiva; si ρXY<0 , diremos que X,Y tienen correlación lineal negativa; si |ρXY|≈1 , diremos que X,Y tienen buena correlación lineal; si ρXY≈0 , diremos que X,Y tienen mala correlación lineal.
Problema 1.21: estudiar la correlación lineal entre el número de calzado y la edad del alumnado asistente a clase; valorarla.
1.5. Estimar si un conjunto de muestras pertenecen a la misma población:
Objetivos:
- Obtener un estimador insesgado de la varianza poblacional a partir de la media de las varianzas de un conjunto de muestras
- Obtener un estimador insesgado de la varianza poblacional a partir de la varianza de las medias de un conjunto de muestras pertenecientes a la misma población.
- Evaluar por análisis de varianza si un conjunto de muestras independientes pertenecen a la misma población.
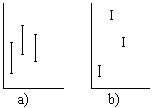 Actividad 1.42. Si tenemos un
conjunto de muestras independientes obtenidas por diferentes
procedimientos,
en caso de que estos procedimientos sean equivalentes la
dispersión
entre las muestras deberá ser proporcionada a la
dispersión
dentro de cada muestra (figura a). A fin de evaluarlo
trabajaremos con m muestras de tamaño n y llamaremos:
Actividad 1.42. Si tenemos un
conjunto de muestras independientes obtenidas por diferentes
procedimientos,
en caso de que estos procedimientos sean equivalentes la
dispersión
entre las muestras deberá ser proporcionada a la
dispersión
dentro de cada muestra (figura a). A fin de evaluarlo
trabajaremos con m muestras de tamaño n y llamaremos:Xjk al elemento k de la muestra j
 j
y s(Xj
j
y s(Xj a la
media
de la muestra de tamaño m·n resultante
de mezclar
las m muestras de tamaño n.
a la
media
de la muestra de tamaño m·n resultante
de mezclar
las m muestras de tamaño n.Demostrar el
Teorema 1.41:
 = ∑
j
= ∑
j  j/m
.
j/m
.Actividad 1.43. Llamaremos varianza dentro de variables a la media de las varianzas sw2 = ∑ j s(Xj
Supondremos que todas las muestras pertenecen a poblaciones por lo menos con la misma varianza σ2 .
Demostrar el
Teorema 1.42: μ(sw2) = σ2·(n-1)/n .
Llamaremos por lo tanto varianza corregida dentro de variables a
 w2
= sw2·n/(n-1), que
será un estimador insesgado de la varianza
poblacional σ2
.
w2
= sw2·n/(n-1), que
será un estimador insesgado de la varianza
poblacional σ2
.Actividad 1.44. Teniendo en cuenta el
Teorema 1.43: si las variables aleatorias independientes Y1, Y2 tienen distribución Ji-cuadrado con grados de libertad ν1 y ν2 respectivamente, entonces la variable aleatoria Y1+Y2 tiene distribución Ji-cuadrado con ν1+ν2 grados de libertad
demostrar el
Teorema 1.44: mn·sw2/σ2 tiene distribución Ji-cuadrado con m·(n-1) grados de libertad
Actividad 1.45. Llamaremos
μj=μ(Xj
μ=μ(X) a la media de la población resultante de mezclar las poblaciones a las que pertenecen las m muestras
αj=μj-μ para cada muestra j (naturalmente, valdrá 0 si todas las muestras pertenecen a la misma población).
Demostrar que en cualquier caso se cumple el
Teorema 1.45: ∑ j αj = 0 .
Actividad 1.46. Llamaremos varianza entre variables a la varianza de las medias
sb2 = ∑ j (
 j-
j- )2/m
= ∑ j
)2/m
= ∑ j  j2/m
-
j2/m
-  2
.
2
.Recordando de la Actividad 1.26 que σ(
 j)2=σ2/n
, σ(
j)2=σ2/n
, σ( )2=σ2/(mn),
demostrar
)2=σ2/(mn),
demostrarTeorema 1.46: μ(
 j2)
= σ2/n +
(μ+αj)2.
j2)
= σ2/n +
(μ+αj)2.Teorema 1.47: μ(
 2)
= σ2/(mn) +
μ2.
2)
= σ2/(mn) +
μ2.Teorema 1.48: μ(sb2) = σ2(m-1)/(mn) + ∑ j αj2/m .
Actividad 1.47. Llamaremos varianza corregida entre variables a
 b2
= sb2·nm/(m-1)
.
b2
= sb2·nm/(m-1)
.Demostrar el
Teorema 1.49: μ(
 b2)
= σ2 +
n·∑ j αj2/(m-1)
.
b2)
= σ2 +
n·∑ j αj2/(m-1)
.Por lo tanto,
 b2
será un estimador insesgado de la varianza
poblacional σ2
si y sólo si las poblaciones a las cuales pertenecen las
diferentes muestras
tienen todas la misma media (lo que llamamos hipótesis
nula en
la que todo αj =0),
cosa que naturalmente
pasará si todas las muestras pertenecen a la misma
población. En este caso, F=
b2
será un estimador insesgado de la varianza
poblacional σ2
si y sólo si las poblaciones a las cuales pertenecen las
diferentes muestras
tienen todas la misma media (lo que llamamos hipótesis
nula en
la que todo αj =0),
cosa que naturalmente
pasará si todas las muestras pertenecen a la misma
población. En este caso, F= b2/
b2/ w2
deberá ser próximo a la unidad. En otro caso μ(
w2
deberá ser próximo a la unidad. En otro caso μ( b2)>σ2
, y por lo tanto se puede prever que F sea mayor que la unidad.
b2)>σ2
, y por lo tanto se puede prever que F sea mayor que la unidad.Actividad 1.48. Teniendo en cuenta que sb2 es la varianza de la muestra (
 1,
1,
 2,...
2,... m),
de tamaño m, y que σ(
m),
de tamaño m, y que σ( j)2=σ2/n,
demostrar que si las muestras pertenecen a la misma población
se cumple el
j)2=σ2/n,
demostrar que si las muestras pertenecen a la misma población
se cumple elTeorema 1.50: mn·sb2/σ2 tiene distribución Ji-cuadrado con m-1 grados de libertad.
Actividad 1.49. Teniendo la cuenta el
Teorema 1.51: si las variables aleatorias independientes Y1, Y2 tienen distribución Ji-cuadrado con grados de libertad ν1 y ν2 respectivamente, entonces la distribución de F=(Y1/ν1)/(Y2/ν2) entre 0 y ∞ es
Wν1,ν2(F) = Kν1,ν2·Fν1/2-1/(1+ν1·F/ν2)(ν1+ν2)/2, que se denomina distribución F de Snedecor con grados de libertad ν1 y ν2 . Kν1,ν2 se escoge de modo que ∫0∞ Wν1,ν2(F) dF = 1
demostrar el
Teorema 1.52: si tenemos m muestras independientes de tamaño n pertenecientes a la misma población, entonces
F=
 b2/
b2/ w2
tiene una distribución F de Snedecor con grados de libertad ν1=m-1,
ν2=m·(n-1)
.
w2
tiene una distribución F de Snedecor con grados de libertad ν1=m-1,
ν2=m·(n-1)
.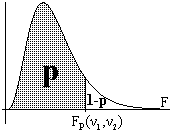 Actividad
1.50. Si tenemos m muestras independientes de tamaño
n y
Actividad
1.50. Si tenemos m muestras independientes de tamaño
n y F=
 b2/
b2/ w2
> Fp(m-1
, m·(n-1)), siendo Fp(ν1, ν2)
el coeficiente crítico de la distribución F de Snedecor
con grados de libertad ν1
y ν2 tal
que la probabilidad de un valor menor o igual a este coeficiente sea
p, entonces podemos rechazar con un nivel de significación
β=1-p la hipótesis nula de que las
muestras pertenezcan a la misma población. Utilizaremos las tablas
de la distribución F de Snedecor (inversa) para
determinar el correspondiente coeficiente crítico.
w2
> Fp(m-1
, m·(n-1)), siendo Fp(ν1, ν2)
el coeficiente crítico de la distribución F de Snedecor
con grados de libertad ν1
y ν2 tal
que la probabilidad de un valor menor o igual a este coeficiente sea
p, entonces podemos rechazar con un nivel de significación
β=1-p la hipótesis nula de que las
muestras pertenezcan a la misma población. Utilizaremos las tablas
de la distribución F de Snedecor (inversa) para
determinar el correspondiente coeficiente crítico.Problema 1.22: anotar el número de calzado en varias muestras del mismo tamaño entre el alumnado asistente a clase y valorar si pertenecen a la misma población (a ser posible, procurar que alguna de las muestras esté formada únicamente por chicos y otra únicamente por chicas).
Actividad 1.51. ¿Cómo habríamos de interpretar el hecho que F=
 b2/
b2/ w2
<< 1? Aplicarlo a la resolución del
siguiente
w2
<< 1? Aplicarlo a la resolución del
siguienteProblema 1.23: calcular el estadístico F correspondiente al siguiente par de muestras:
X1=(24'2, 25'3, 25'4 , 26'2, 27'5)
X2=(24'2, 25'3, 25'4 , 26'2, 27'4)
¿Se puede considerar que las muestras no cumplan alguna de las premises del Teorema 1.52?
Para valorarlo con un cierto nivel de significación podemos utilizar la relación Fp(ν1, ν2)=1/F1-p(ν2, ν1) .
Trabajo 3 (para su realización en equipo):
Comparar diferentes procedimientos para obtener algún preparado químico utilizando alguna variable aleatoria adecuada (cantidad del preparado, tiempo para su obtención, etc.). Obtener los datos de experiencias reales y utilizar un mínimo de 3 procedimientos aplicando como mínimo 5 veces cada procedimiento. Estimar por análisis de varianza si los diferentes procedimientos se pueden considerar equivalentes.
Actividad 1.1: Debatir en grupos pequeños el siguiente texto, escogiendo previamente un portavoz de cada grupo para exponer posteriormente las conclusiones y en su caso las dudas suscitadas:
Desde Leibnitz y Newton, se ha desarrollado fundamentalmente la matemática continua. Esto iba acompañado de una concepción del mundo según la cual las variables reales variarían de forma continua, pero respondía también a razones prácticas: el tratamiento de variables discretas exige un gran número de cálculos para los que no se disponía de instrumentos adecuados, mientras que sí se disponía de poderosos métodos analíticos, de cálculo diferencial e integral, para el tratamiento de variables continuas. Aun así, había un gran número de problemas que no se podían resolver con estos métodos analíticos.
Sin embargo, actualmente la situación ha cambiado radicalmente: por una parte, se reconoce, con una fuerte fundamentación en la mecánica cuántica, que, dadas las limitaciones en la precisión de los datos experimentales, siempre trabajamos realmente con variables discretas; y por otra parte, el uso de los ordenadores permite la realización de los cálculos masivos necesarios para el tratamiento de estas variables discretas.
El cálculo numérico consiste en una serie de métodos para obtener aproximaciones discretas a la solución de diferentes problemas.
Así, si tenemos los valores de f(xi) para determinados valores de xi , buscaremos aproximar por interpolación el valor de f(x) para un nuevo valor de x; se pueden utilizar diferentes funciones de interpolación, dependiendo de la estimación que se haga de las características de f(x); en este curso aproximaremos únicamente mediante funciones polinómicas, haciendo lo que se denomina interpolación polinómica. Pero si el nuevo valor de x se encuentra fuera del intervalo delimitado por los xi previamente estudiados, estaremos haciendo realmente una extrapolación: la aproximación polinómica de f(x) nos dará entonces una hipótesis a contrastar con nuevos datos.
Igualmente, hay muchos problemas de integración que no se pueden resolver de forma analítica, es decir, no podemos obtener una función integral continua y=F(x) la derivada de la cual satisfaga las condiciones del problema. Pero podremos aun así encontrar soluciones aproximadas de su valor numérico para valores particulares de x.
2.1. Interpolar el valor de una función polinómica desconocida que pase por un conjunto de puntos:
Objetivos:
- Demostrar la existencia y unicidad del polinomio interpolador de grado menor o igual que m que pasa por m+1 puntos de abcisas distintas.
- Encontrar una fórmula que nos dé directamente la expresión del polinomio interpolador.
- Encontrar un método para obtener sucesivamente puntos interpolados a medida que introducimos nuevos puntos para interpolar.
- Encontrar un método que nos dé sucesivos
términos del polinomio interpolador.
- Entender los problemas de fiabilidad
de la interpolación, especialmente si se realiza fuera
del intervalo en el cual se tienen datos (extrapolación) o se
utilizan
polinomios de un grado elevado.
Teorema -2.1: |xki| = ∏ k>i (xk-xi)
y la
Definición 2.1: diremos que p(x) = ∑ i=0 m ai xi es un polinomio interpolador de grado menor o igual que m en los puntos
{(xk,fk) / k=0,1...m} si y sólo si, para todo k=0,1...m, p(xk)=fk ,
demostrar el
Teorema 2.1: si para todo i≠k, xi≠xk, entonces existe un único polinomio interpolador de grado menor o igual que m en los puntos {(xk,fk) / k=0,1...m} .
Actividad 2.3. Teniendo en cuenta que
∑ i=0 m Ξi = Ξk + ∑ i≠k Ξi para todo k=0,1...m, y que
∏ j≠i Ξkj = Ξkk·∏ j≠i & j≠k Ξkj para todo i≠k.
demostrar el
| Teorema 2.2: si para todo i≠k, xi≠xk, entonces p(x) = ∑ i=0 m fi | ∏ j≠i (x-xj) ∏ j≠i (xi-xj) |
Actividad 2.4.
Problema 2.1: dados los puntos
| x k. |
1. |
2. |
4. |
5. |
| f k |
0. |
2. |
12. |
21. |
(sugerencia: al aplicar la fórmula, escribir primero cada denominador para evitar errores)
Actividad 2.5. Demostrar el
Teorema 2.3: si para todo i,j=0,1...m, si i≠k, entonces xi≠xk,
& si i+j≤m , entonces pi,j es el polinomio interpolador de grado menor o igual que j en {(xk,fk) / k=i,i+1...i+j},
entonces para todo j=1...m, i=0,1...m-j,
| pi,j(x)
= |
(xi+j-x)pi,j-1
+ (x-xi)pi+1,j-1. xi+j - xi |
Actividad 2.6. Teniendo en cuenta que, con los pi,j definidos en el Teorema 22,
Teorema 2.4: para todo y=0,1...m & para todo xcR, pi,0(x) = f i
y
Teorema 2.5: p0,m es el polinomio interpolador de grado menor o igual que m en {(xk,fk) / k=0,1...m} ,
utililizar el algoritmo
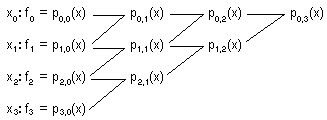 (método
de Neville)
(método
de Neville)para resolver el
Problema 2.2: dados los puntos
| x k |
1. |
2. |
4. |
| f k |
0. |
2. |
12. |
Añadir a continuación el punto (x3, f3) = (5, 21) y obtener la nueva interpolación para x=3 .
Comparar el resultado obtenido con el del problema 2.1.
Actividad 2.7. De acuerdo con la
Definición 2.2: con {(xk,fk) / k=0,1...m} tal que para todo i,j=0,1...m, si i≠k, entonces xi≠xk, definiremos las diferencias divididas f[xi,xi+1,...xj] mediante| f[xi] = | fi | para
todo i=0,1...m |
| f[xi,xi+1,xj]
= |
ff[xi+1,...xj]
- f[xi,...xj-1] xj - xi |
para todo i=0,1...m-1
, j=i+1,...m |
| f[x0] f[x1] f[x2] f[x3] |
> f[x0,x1] > f[x1,x2] > f[x2,x3] |
> f[x0,x1,x2] > f[x1,x2,x3] |
> f[x0,x1,x2,x3] |
| k. |
0. |
1. |
2. |
3. |
| x k |
1. |
2. |
4. |
5. |
| f k |
0. |
2. |
12. |
21. |
pm(x) = ∑j=0 m f[x0,...xj] ∏i=0 j-1 (x-xi )
es el polinomio interpolador de grado menor o igual que m en {(xk,fk) / k=0,1...m} (método de Newton )
Actividad 2.8. Asumiendo que el error de la interpolación polinómica de grado menor o igual que m viene dada por
Teorema -2.2: f(x)-pm(x) = [f (m+1)(ξ(x))/(m+1)!] ∏i=0 m (x-xi) tal que ξ(x)c[a,b] tal que para todo i=0,1...m, xic[a,b]
Problema 2.4: acotar el valor de f(3) suponiendo que
| x k |
1. |
2. |
4. |
5. |
| f(x k) |
0. |
2. |
12. |
21. |
2.2. Aproximar la integración de una función, acotando el error de aproximación:
Objetivos:
- Obtener unos pesos Wk independientes de la función f(x) tales que sumando su producto por los correspondientes valores de la función en determinados nodos xk, ∑ k=0 m Wk f(xk), proporcione la integral exacta para polinomios hasta un cierto grado, y una buena aproximación para otras funciones.
- Aprender a acotar el error de esta aproximación expresándolo como el producto de un factor C independiente de la función f(x) por la derivada de un cierto orden r de la función en algún punto ξ del intervalo de integración [a,b] , Cf(r)(ξ).
- Estudiar el caso de nodos equidistantes, xk=a+kh (Fórmula de Newton-Cotes).
- Aprender a mejorar la aproximación aumentando el número de nodos.
- Utilizar el método de coeficientes indeterminados para obtener tanto los pesos Wk de integración como el factor C del error, a partir de la integral exacta de potencias simples y resolviendo en grupos pequeños los correspondientes sistemas de ecuaciones para exponer públicamente a continuación los resultados obtenidos.
Definición 2.3: siendo f:[a,b]→R una función integrable, llamaremos integral numérica polinómica de f en los nodos xk tales que a≤x0<...<xm≤b a la integral en el intervalo [a,b] del polinomio interpolador de grado menor o igual que m en los puntos {(xk,f(xk)}k=0,1...m
y utilizando la expresión del polinomio interpolador proporcionada por el método de Lagrange, justificar la existencia de unos pesos Wk independientes de la función f(x) con los cuales ∑ k=0 m Wk f(xk) sea su integral numérica polinómica.
Actividad 2.10. Teniendo en cuenta que una integral numérica polinómica en m+1 nodos es igual a la integral exacta para polinomios de grado menor o igual que m, encontrar un sistema de ecuaciones para la obtención de los pesos Wk y demostrar que si para todo i≠k, xi≠xk, este sistema de ecuaciones tiene solución única.
Teorema -2.3: ∫a b f(x) dx = ∫u-1(a) u-1(b) f(u(t)) u'dt
demostrar el
Teorema 2.6: en el caso de nodos equidistantes x k=a+kh, con k=0,1...m, h=(b-a)/m, demostrar que los pesos para el cálculo de la correspondiente integral numérica polinómica (pesos de Newton-Cotes) tienen la forma Wk=hW'k(m), dónde W'k(m), que son los pesos correspondientes al caso h=1, sólo dependen de k y de m (pero no de a y de b ).
Puede utilizarse para la demostración la expresión de los pesos Wk obtenida en la Actividad 2.9, aplicando en la correspondiente integral el cambio de variable x=a+th .
Actividad 2.12. Obtener los pesos de Newton-Cotes para m=2 y el intervalo [0,2]. A partir de los mismos, obtener la fórmula general (Fórmula de Simpson) para la integral numérica polinómica en los nodos {a, a+h, a+2h} = {a, (a+b)/2, b},
S =
Actividad 2.13.
Problema 2.5: aproximar mediante la Fórmula de Simpson ∫-1 1 e x2 dx .
Actividad 2.14. Teniendo en cuenta la expresión del error de la interpolación polinómica de grado menor o igual que m dada por el Teorema -2.2 , así como que
Teorema -2.4: para
toda función integrable f:[a,b]→R, |∫a b
f(x)dx|
≤ ∫a b |f(x)|dx .
Teorema -2.5: para
todo par de funciones integrables f:[a,b]→R, g:[a,b]→R+,
existe ξc[a,b]
tal
que
demostrar el
Teorema 2.7: el valor absoluto del error de la integral numérica polinómica en m+1 nodos puede acotarse por el producto de dos factores, uno de los cuales depende únicamente de los nodos, y el otro depende únicamente de la derivada de orden m+1 en algún punto ξ del intervalo de integración [a,b].
Actividad 2.15. Suponiendo que el error de un método de integración aproximada sea de la forma
NOTA: en caso de obtenerse C=0 puede inferirse que el método es exacto para esta función, y deberá repetirse el proceso sustituyendo r por r+1 .
Actividad 2.16. Teniendo
en cuenta el
| Teorema -2.6: para todo fcC r(R→R),
xcC1(R→R),
|
dr f
dtr |
(x(t)) = ﴾dx/dt﴿r |
dr f
dxr |
(x) |
Teorema 2.8: si la expresión del error para aproximar ∫0 m f(t)dt con nodos equidistantes y h=1 es
| ε' = C' | dr f dtr |
(ζ) para algún ζc[0,m], |
| ε = C. | dr f dxr |
(ξ) para algún ξc[a,b] con C=hr+1 C' |
Actividad 2.17. Obtener la expresión del error para la Fórmula de Simpson para el intervalo [0,2] (con h=1), y a partir de ella obtener la expresión general del error para la Fórmula de Simpson para el intervalo [a,b] (con h=(b-a)/2),
εS =
Indicar para qué polinomios será exacta esta fórmula.
Actividad 2.18.
Problema 2.6: acotar el error de la Fórmula de Simpson aplicada a ∫-1 1 e x2 dx . Valorarlo.
Actividad 2.19. Teniendo
en cuenta la
Definición 2.4:
siendo f:[a,b]→R una función integrable, denominaremos integral numérica compuesta
de grado m en los mM+1 nodos
{a+kh}k=0,1...mM , con h=(b-a)/(mM), a.
demostrar el
Teorema 2.9: para toda función integrable f:[a,b]→R , su integral numérica compuesta de grado 2 en los 2M+1 nodos {a+kh}k=0,1...2M , con h=(b-a)/(2M), (regla de Simpson) viene dada por
= [f(a) + f(b) + ∑i=1 M-1 2f(a+2ih) + ∑i=0 M-1 N4f(s+(2i+1)h)](b-a)/(6M)
Actividad 2.20. Teniendo en cuenta el
Teorema -2.7: para toda función continua f:[a,b]→R y todo conjunto de puntos ξ ic[a,b], i=1...n, existe ξc[a,b] tal que
Teorema 2.10: para toda fcC4([a,b],R), el error de la regla de Simpson para aproximar ∫a b f(x)dx viene dado por
Actividad 2.21.
Problema 2.7: ¿qué incremento h deberemos tomar para obtener una aproximación a ∫-1 1 e x2 dx con un error menor a 0'01 mediante la regla de Simpson?
 Trabajo 4
(para
su realización en equipo):
Trabajo 4
(para
su realización en equipo):Obtener los coeficientes W0, W1 que hacen que
Utilizarlo para acotar ∫0 10 (225+x3)½dx a sabiendas de que |f "(x)|<0'6 en este intervalo.
2.3. Obtener el valor futuro de una variable conociendo su valor inicial y la dependencia de su derivada respecto del tiempo y la misma variable, y'=f(t,y):
Objetivos:
- Aproximar soluciones de una ecuación diferencial a partir de unas condicionas iniciales sustituyendo el incremento por la diferencial (MÉTODO DE EULER).
- Obtener una aproximación de segundo orden a las soluciones de una ecuación diferencial (MÉTODO DE RUNGE).
- Generalizar la Fòrmula de Simpson para integrar ecuaciones diferenciales (MÉTODO DE RUNGE-SIMPSON).
- Obtener una aproximación de cuarto orden a las soluciones de una ecuación diferencial (MÉTODO DE KUTTA).
 Actividad
2.22. Si conocemos y'=f(t,y) así como la
condición
inicial y0=y(t0),
teniendo en cuenta el
Actividad
2.22. Si conocemos y'=f(t,y) así como la
condición
inicial y0=y(t0),
teniendo en cuenta elTeorema -2.8: si y(t) es una función derivable hasta el segundo orden,
y(t) = y(t0) + y'(t0)·∆t + y"(ξ)·(∆t)2/2 tal que ξc[t0, t]
se cumplirá y(t) = y0 + f(t0,y0)·∆t + Θ·(∆t)2 . Así pues
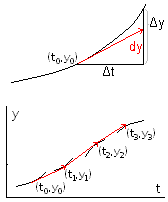
Problema 2.8: aplicar el método de Euler para aproximar el valor de y cuando t=1 conociendo que y=1 cuando t=0 y que y'=0'1y2-ty. Tomar ∆t=0'2 y representarlo gráficamente.
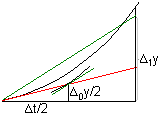 Actividad
2.23.
El método de Euler daría un resultado exacto si la
derivada y',
representada por la pendiente de la curva, fuera constante (y por lo
tanto la segunda
derivada valiera cero). Si no es así, encontraremos
que la derivada
en el punto (t1,y1)
será f(t1,y1)=f(t0+∆t,y0+∆0y)≠f(t0,y0).
En este caso, podemos obtener una mejor aproximación si
calculamos
la derivada en el punto intermedio (t0+∆t/2,y0+∆0y/2)
y tomamos y1=y0+∆1y
con ∆1y=f(t0+∆t/2,y0+∆0y/2)·∆t,
y así sucesivamente (método
de Runge de segundo orden); en este caso el error es
proporcional a (∆t)3 .
Actividad
2.23.
El método de Euler daría un resultado exacto si la
derivada y',
representada por la pendiente de la curva, fuera constante (y por lo
tanto la segunda
derivada valiera cero). Si no es así, encontraremos
que la derivada
en el punto (t1,y1)
será f(t1,y1)=f(t0+∆t,y0+∆0y)≠f(t0,y0).
En este caso, podemos obtener una mejor aproximación si
calculamos
la derivada en el punto intermedio (t0+∆t/2,y0+∆0y/2)
y tomamos y1=y0+∆1y
con ∆1y=f(t0+∆t/2,y0+∆0y/2)·∆t,
y así sucesivamente (método
de Runge de segundo orden); en este caso el error es
proporcional a (∆t)3 .Problema 2.9: aplicar el método de Runge de segundo orden para aproximar el valor de y cuando t=0'4 conociendo que y=1 cuando t=0 y que y'=0'1y2-ty. Tomar ∆t=0'2.
Actividad 2.24. Con el método de Runge de segundo orden hemos mejorado la aproximación calculando un nuevo incremento para la función y a partir de un punto auxiliar (en este caso, intermedio). Podemos obtener mejores aproximaciones escogiendo sucesivamente de forma adecuada nuevos puntos auxiliares. En particular, si tomamos sucesivamente
∆IIy=f(t0+∆t, y0+∆Y y)·∆t
obtendremos una aproximación de tercer orden, con error proporcional a (∆t)4, si tomamos
t1=t0+∆t, y1 = y0 + ∆0y/6 + 4·∆1y/6 + ∆IIy/6 y así sucesivamente (método de Runge-Simpson).
Comprobar que en el caso particular en que tengamos y'=f(x), este método es equivalente a la Fórmula de Simpson.
Actividad 2.25. Podemos obtener una aproximación de cuarto orden, con error proporcional a (∆t)5, si tomamos
∆2y=f(t0+∆t/2,y0+∆1y/2)·∆t
∆3y=f(t0+∆t, y0+∆2y)·∆t
y finalmente
t1=t0+∆t, y1 = y0 + ∆0y/6 + ∆1y/3 + ∆2y/3 + ∆3y/6 y así sucesivamente (método de Kutta de cuarto orden).
Tenemos recopilados los diferentes métodos en el siguiente diagrama de flujos:
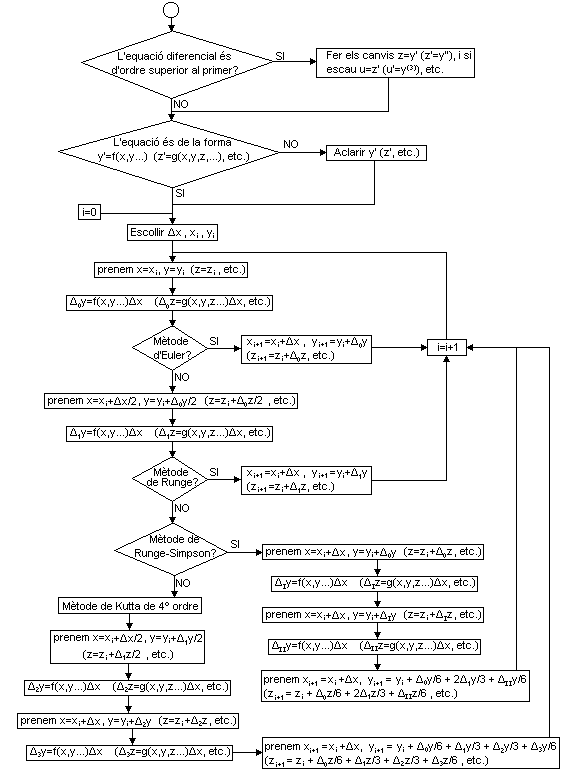
Podemos utilizar también el siguiente diagrama a fin de recordar a partir de qué incremento se obtiene un nuevo incremento (con incremento total o con medio incremento) y qué coeficientes hemos de utilizar para obtener el incremento final:
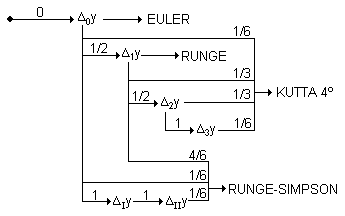
Para el método de Kutta de cuarto orden podemos realizar los cálculos en la siguiente tabla:
| ty yy |
t0. y0. |
t1 = t0+∆t y1 = y0 + ∆0y/6 + ∆1y/3 + ∆2y/3 + ∆3y/6. |
|||
| t y y' ∆0y ∆1y ∆2y ∆3y |
t0. y0. f(t,y) ∆0y |
t0+∆t/2. y0+∆0y/2. f(t,y) ∆1y |
t0+∆t/2. y0+∆1y/2. f(t,y) ∆2y |
t0+∆t y0+∆2y f(t,y) ∆3y |
|
Naturalmente, en el momento de aplicar las tablas las expresiones se sustituyen por números.
Problema 2.10: aplicar el método de Kutta de cuarto orden para aproximar el valor de y cuando t=0'6 conociendo que y=1 cuando t=0 y que y'=0'1y2-ty. Tomar ∆t=0'2.