GUIA DIDÀCTICA
Rafael Pla López
Departament de Matemàtica Aplicada
Universitat de València
2010
Objectius:
Específics:
- Estimar els diferents tipus d'error que es produeixen en la resolució de problemes per mètodes numèrics.
- Obtenir aproximacions successives a la solució d'un sistema d'equacions lineals Ax=b.
- Resoldre per aproximacions successives una equació no lineal del tipus f(x)=0.
- Trobar una funció polinòmica que passe per un conjunt de punts.
- Obtenir una solució aproximada de la integral definida d'una funció, ∫a b f(x)dx
- Aprendre a treballar en equip.
- Aprendre a exposar públicament un treball.
- Adquirir respecte pels companys que exposen un treball, atenent-los i ajudant-los en cas necessari.
- Aprendre a realitzar raonaments deductius per a demostrar un enunciat a partir de determinades premisses.
- Adquirir la capacitat de qüestionar la fiabilitat dels resultats obtinguts per mètodes numèrics.
Metodologia:
- Treball en classe en grups menuts debatint textos, demostrant enunciats i resolent problemes, seguit de la seua exposició pública.
- Treball en equip fora de classe, elaborant treballs per a la seua presentació al professor.
- Treball pràctic en aula d'informàtica, confeccionant programes per a la resolució de problemes, executant-los per a obtenir els seus resultats, i valorant aquests resultats, reflectint tot això en una memòria de cada pràctica.
- Aubanell, A., Benseny, A., Delshams, A. (1991), Eines bàsiques de Càlcul Numèric, Universitat Autònoma de Barcelona, Bellaterra
- Aubanell, A., Benseny, A., Delshams, A. (1993), Útiles básicos de Cálculo Numérico, Editorial Labor, Barcelona
- Conte, S.D., de Boor, C. (1985), Análisis Numérico, McGraw-Hill, México
- Martínez Salas, J. (1989), Métodos Matemáticos, Ed.el autor, Valladolid
- Arándiga, F. (2002), Càlcul Numèric, Departament de Matemàtica Aplicada, Universitat de València
- La qualificació final serà la mitjana de la nota de teoria i la nota de pràctiques, sempre que ambdues siguen igual o superior a 4 (sobre un màxim de 10).
- Per a la nota de teoria puntuarà fins a 8 punts l'avaluació d'un examen final individual escrit, i fins a 2 punts la realització de treballs en equip, que solament podran considerar-se en cas d'assistència regular a classe (en cas contrari, haurien de respondre's qüestions addicionals en l'examen final puntuables fins als 2 punts restants). Es podrà utilitzar un formulari escrit a ma personalment en un màxim de 5 fulls sense problemes resolts (no s'admeten fotocòpies). A més, es prevaldrà la participació activa en classe sumant una dècima per cada exposició pública d'un treball realitzat en classe.
- Per a la nota de pràctiques, sobre la base de
l'assistència
obligatòria a les mateixes, es valorarà la memòria
presentada de
cada pràctica, que haurà de contenir els programes
elaborats, els resultats obtinguts amb ells i la valoració
dels mateixos.
Tema 0: Estimar els diferents tipus d'error que es
produeixen en
la resolució de problemes per mètodes numèrics:
Objectius:
- Comprendre la diferència entre errors intrínsecs i instrumentals.
- Comprendre els conceptes d'error absolut i error relatiu.
- Entendre com tracten els ordinadors els nombres no sencers.
- Estimar quantes xifres significatives es coneixen d'una determinada quantitat.
- Debatre un text en grups menuts, posant posteriorment en comú el resultat del debat.
- Realització de tasques en grups menuts, exposant públicament a continuació les seues conclusions.
Activitat 1. Debatre en grups menuts el següent text, escollint prèviament un portaveu de cada grup per a exposar posteriorment les conclusions i si escau els dubtes suscitats:
Els mètodes numèrics permeten obtindre solucions aproximades a determinats problemes. Per avaluar aquestes solucions, és important tindre una estimació de l'error.
Hi ha errors intrínsecs al mètode utilitzat. Normalment aquests errors es poden fer tan petits com es vulga, a través d'aproximacions successives. Tanmateix, al disposar d'un temps finit per realitzar els càlculs, hem de conformar-se amb aproximar amb un cert marge d'error. Caldrà, doncs, un compromís entre la cota d'error admesa i el temps màxim de càlcul que ens podem permetre.
Naturalment, seran preferibles aquells mètodes que permetan aproximar fins a una determinada cota d'error en menys temps, els quals direm que tenen una velocitat de convergència major. En els mètodes que aproximen iterativament a través d'una sèrie de passos successius, podem mesurar aquesta velocitat per la inversa del número de passos necessaris. Tanmateix, des del punt de vista del temps de càlcul cal valorar també la complexitat dels càlculs a realitzar en cada pas.
Als efectes anteriors, normalment treballarem amb l'error absolut, definit com el valor absolut de la diferència entre el valor exacte x i l'aproximació
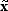 ,
, Definició 1: ε = | x -
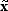 |
| Naturalment, en desconèixer el valor exacte l'únic que podrem fer és estimar l'error, donant una cota superior per al mateix.
Hi ha també errors instrumentals deguts a l'instrument de càlcul utilitzat. En particular, les calculadores i ordinadors digitals treballen amb un número finit de xifres, i per tant no utilitzen números amb infinites xifres decimals, com els irracionals o els fraccionaris "decimals periòdics". Per exemple, aproximarien 1/3 = 0' 3 ≈ 0'333333 , amb un número de xifres decimals depenent de la precisió de l'instrument.
Per aproximar el càlcul dels números racionals i reals, els ordinadors treballen amb números decimals en punt flotant, tractant per separat les xifres significatives (mantissa) i l'ordre de magnitud (característica). Per exemple, 0'0000000000000235410347= 2'35410347.10-14 s'expressarà com 2.35410347E-14.
Per tal com la principal limitació està en el número de xifres significatives admeses, allò que ens importarà serà l'error relatiu del valor aproximat
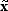 respecte del valor exacte x, definit com
respecte del valor exacte x, definit comDefinició 2: εr = | x -
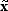 | /
| x |
| /
| x |
Activitat 2. Obtenir una
fórmula que coneixent l'error relatiu i la mantissa ens
proporcione el nombre de xifres significatives exactes que
coneixem, d'acord amb la
Definició 3:
Direm que 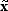 =aEb
(amb 1≤
a< 10) aproxima a x amb un
nombre sencer de
k xifres significatives si i només si
=aEb
(amb 1≤
a< 10) aproxima a x amb un
nombre sencer de
k xifres significatives si i només si
L'obtenció d'aquesta fórmula ens permetrà completar l'enunciat del següent
Teorema 1:
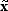 =aEb aproximarà a x amb un nombre de xifres
significatives exactes k igual
al major nombre sencer menor que
=aEb aproximarà a x amb un nombre de xifres
significatives exactes k igual
al major nombre sencer menor que Com podríem interpretar el cas que k resultara negatiu?
Activitat 3.
Problema 1: calcular l'error absolut i relatiu en els següents casos:
a)
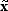 =
2.35410347I-14 , x = 2.35410343I-14.
=
2.35410347I-14 , x = 2.35410343I-14.b)
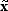 =
2.35410347I16 , x = 2.35410343I16.
=
2.35410347I16 , x = 2.35410343I16.Amb quantes xifres significatives aproxima
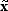 a x
?
a x
?Treball 1 (per a la seua realització en equip):
a) Ampliar la classificació dels errors plantejada en l'Activitat 1 a partir de la bibliografia recomanada.
b) Posar diferents exemples d'aproximació de
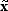 a x
amb diferents errors absoluts i relatius i calcular el nombre
de xifres
significatives amb que s'aproxima en cada cas. Avaluar de què
depèn aquest nombre. Considerar algun cas que l'error
relatiu
siga major a 0'5 i valorar-lo.
a x
amb diferents errors absoluts i relatius i calcular el nombre
de xifres
significatives amb que s'aproxima en cada cas. Avaluar de què
depèn aquest nombre. Considerar algun cas que l'error
relatiu
siga major a 0'5 i valorar-lo.
Tema 1: Obtenir aproximacions successives a la solució d'un sistema d'equacions lineals Ax=b :
Objectius:
- Trobar criteris de convergència per a una transformació x(k+1) = G(x(k)) tal que A(lim k→∞ x(k)) = b
- Trobar una condició suficient per a l'existència d'una solució única d'una equació d'iteració lineal de punt fix x=Bx+c.
- Trobar criteris de convergència per a una iteració lineal de punt fix x=Bx+c.
- Transformar un sistema d'equacions lineals Ax=b en una iteració lineal de punt fix x=Bx+c equivalent
- Trobar una condició suficient perquè aquesta transformació genere una iteració lineal de punt fix convergent
- Aproximar iterativament la solució d'un sistema d'equacions lineals Ax=b utilitzant com aproximació a la matriu A la seua matriu diagonal D (mètode de Jacobi)
- Obtenir la iteració lineal de punt fix equivalent al sistema Ax=b pel mètode de Jacobi.
- Trobar una condició per a la matriu A que garantisca que aquesta iteració lineal de punt fix siga convergent.
- Avaluar un sistema d'equacions lineals i adaptar-lo si escau perquè complisca la condició de convergència
- Aproximar iterativament la solució d'un sistema d'equacions lineals Ax=b utilitzant com aproximació a la matriu A la seua matriu triangular inferior L+D (mètode de Gauss-Seidel)
- Trobar una expressió simplificada en funció de L, D i U de la matriu B de la iteració lineal de punt fix x=Bx+c, equivalent al sistema Ax=b amb A=L+D+U, obtinguda pel mètode de Gauss-Seidel.
- Trobar una expressió que ens permeta calcular successivament els diferents components del vector x(k+1) .
- Discutir la convergència de la iteració lineal de punt fix obtinguda pel mètode de Gauss-Seidel
- Deduir enunciats lògicament, treballant en la mesura del possible en grups menuts per a exposar públicament a continuació la seua demostració.
- Resoldre problemes en grups menuts i exposar públicament a continuació la seua resolució.
- Treballar en aula d'informàtica elaborant programes per a la resolució iterativa de sistemes d'equacions lineals, executant-los per a la resolució d'un sistema determinat i avaluant la seua velocitat de convergència.
Activitat 1 . Definint la norma matricial associada a una norma vectorial per
Definició 4: ||A|| = max x≠0 ||Ax||/||x||
amb el que es compleix
Teorema 2: ||Bx|| ≤ ||B||·||x||
demostrar per reducció a l'absurd que
Teorema 3: Si ||B||<1& x=Bx , llavors x=0.
Activitat 2 . Recordant quina és la condició necessària i suficient perquè:
a) un sistema homogeni d'equacions lineals com x=Bx tinga solució única x=0.
b) un sistema inhomogeni d'equacions lineals com x=Bx+c tinga solució única,
demostrar que
Teorema 4: Si ||B||<1 , llavors x=Bx+c té solució única
Activitat 3 . Recordant que,
per les propietats dels nombres
naturals, haurem demostrat per inducció matemàtica
que una propietat es compleix per a tot
nombre natural k si es compleix per a k=0 i podem demostrar que,
suposant que es compleix per a k, es complirà per a k+1, [p0
& (k) (pk→ pk+1)]→
(k) pk , demostrar que
Teorema 5: Si x=Bx+c
& per a tot nombre natural k, x(k+1)=Bx(k)+c,
llavors per a tot nombre natural k, x-x(k)=Bk(x-x(0))
.
Activitat 4 . Recordant que
podem deduir que una successió no negativa tendirà a
zero si està
fitada superiorment per altra successió que tendeix a zero,
demostrar que
Teorema 6: Si
||B||<1 & per a tot nombre natural k, x(k+1)=Bx(k)+c,
llavors existeix x tal que
x=Bx+c & x=lim k→∞ x(k)
.
Activitat 5 . Recordant que, si
x=Bx+c & x(k)=Bx(k-1)+c,
llavors x-x(k)=B(x-x(k-1)),
així com la propietat triangular
Teorema -1: ||x-x(k-1)||
≤ ||x-x(k)|| + ||x(k)-x(k-1)||
demostrar que
Teorema 7: Si x=Bx+c
& x(k)=Bx(k-1)+c
& ||B||<1, llavors podem fitar l'error d'aproximació
de x(k) a x per
||x-x(k)|| ≤ ||x(k)-x(k-1)||·||B||/(1-||B||)
.
Activitat 6 . Demostrar que,
sent I=(δij)i,j=1...n
la matriu identitat (els elements de la qual valen 1 si i=j i 0 si i≠j)
i A, B,
C matrius n per n, es compleix que
Teorema 8: Si B=I-C-1A
&
c=C-1b, llavors x=Bx+c és equivalent a Ax=b .
Activitat 7 . Demostrar que,
definint
Definició 5: C
és una bona aproximació a A, C≈A, si i només si
||I-C-1A||<1
es compleix que
Teorema 9: Si C≈A
&
B=I-C-1A & c=C-1b & per a tot
nombre natural k, x(k+1)=Bx(k)+c,
llavors
A(lim k→∞ x(k))=b
.
Activitat 8 . Recordant que la
inversa de la matriu diagonal D=((δijAii)i,j=1...n
és
Teorema -2: D-1=((δij/Aii)i,j=1...n
que els productes matricials es calculen mitjançant (XY)ij=∑
k
XikIkj
i que ∑ k δikXk
= Xi, demostrar que
Teorema 10: Si C=D
& B=I-C-1A & c=C-1b , llavors, per a tot
i,j=1...n, ci=bi/Aii
& Bij = -Aij/Aii
si i≠j & Bij=0 si i=j .
Activitat 9 . Obtenir
l'expressió
de la iteració corresponent al
mètode de Jacobi,
Teorema 11: x(k+1)i
=
Activitat 10 . A partir de les
següents definicions:
Definició 6:
Direm que la matriu A és estrictament diagonalment dominant per
files si i només si, per a tot
i=1...n, |Aii| > ∑ j≠i |Aij|
Definició 7:
||x||∞ = max i |xi|
i sabent que
Teorema -3: ||A||∞
= max i ∑ j=1n |Aij|
demostrar que
Teorema 11: Si la
matriu A és estrictament diagonalment dominant per files,
llavors
la iteració corresponent al mètode de Jacobi és
convergent.
Activitat
11.
Problema 2:
Aproximar la solució del sistema d'equacions
{10x1+x2+x3=12
, x1+10x2+x3=12
, x1+x2+10x3=12}
pel mètode de Jacobi: iterar des de (x1,x2,x3)=(0,0,0)
fins que ||x(k)-x(k-1)||∞<0.005
; fitar l'error.
Què passaria si prenguérem el sistema d'equacions
{x1+10x2+x3=12
, x1+x2+10x3=12
, 10x1+x2+x3=12}?
Activitat 12 . Sent Lij=Aij
si i>j, Lij=0 si i≤j, Uij=Aij
si i<j, Uij=0 si i≥j, de manera que
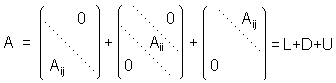
Teorema 12: Si C=L+D & B=I-C-1A, llavors B=
Activitat 13 . Recordant que c=C-1b, obtenir l'expressió matricial de la iteració corresponent al mètode de Gauss-Seidel,
Teorema 13: x(k+1) =
Activitat 14 . Per a evitar el càlcul, no trivial, de (L+D)-1, aplicar D-1(L+D) a ambdós termes de l'expressió anterior i reescriure l'expressió resultant en la forma
Teorema 14: x(k+1) = D-1( )
Activitat 15 . Obtenir una expressió que ens permeta calcular successivament els diferents components
Teorema 15: x(k+1)i =
Desenvolupar aquesta expressió per al cas n=3.
Activitat 16 . Discutir les condicions de convergència del mètode de Gauss-Seidel.
Activitat 17.
Problema 3: Aproximar la solució del sistema d'equacions
{10x1+x2+x3=12 , x1+10x2+x3=12 , x1+x2+10x3=12} pel mètode de Gauss-Seidel: iterar des de (x1,x2,x3)=(0,0,0) fins que ||x(k)-x(k-1)||∞<0.005 ; comparar la seua velocitat de convergència amb la del mètode de Jacobi.
Treball 2 (per a la seua realització en equip):
Aproximar la solució del sistema d'equacions {3x+y=4, x+2y=3} pel mètode de Jacobi a partir de x(0)=(1,3) i de x(0)=(10,0) fins que es complisca ||x(k)-x(k-1)||∞<0.05 , representant gràficament en el plànol els successius punts trobats.
Aproximar aquesta solució pel mètode de Gauss-Seidel a partir de x(0)=(1,3), representant gràficamente en el plànol els successius punts trobats.
Aplicar el mètode de Jacobi a partir de x(0)=(1,3) amb el sistema escrit d'aquesta forma: {x+2y=3, 3x+y=4}, representant gràficamente en el plànol els successius punts trobats.
Comparar les diferents iteracions, valorant la seua convergència.
Tema 2: Resoldre per aproximacions successives una equació no lineal del tipus f(x)=0 :
Objectius:
- Desenvolupar un algorisme que ens permeta anar fitant en intervals cada vegada més menuts una solució de l'equació f(x)=0 tenint en compte el signe de f(x) en els extrems d'un interval.
- Desenvolupar un algorisme que ens permeta anar aproximant-nos cada vegada més a una solució de l'equació f(x)=0 tenint en compte el valor de f(x) en els extrems d'un interval.
- Desenvolupar un algorisme que ens permeta anar fitant en intervals tan menuts com vulguem una solució de l'equació f(x)=0 tenint en compte el valor de f(x) en els extrems d'intervals successius.
- Desenvolupar un algorisme que ens permeta anar aproximant-nos cada vegada més a una solució de l'equació f(x)=0 tenint en compte el valor de f(x) en un punt i la seua derivada.
- Entendre les dificultats
que es troben amb els diferents algorismes per a aproximar-se o
fitar una solució de l'equació f(x)=0.
- Estudiar la velocitat de convergència d'una successió que tendisca a una solució de l'equació f(x)=0.
- Desenvolupar un algorisme que permeta convergir el més ràpidamente possible cap a una solució de l'equació f(x)=0.
- Reflexionar col·lectivament, en grups menuts i en el conjunt de la classe, sobre diferents procediments per a aproximar-se a una solució de l'equació f(x)=0.
- Deduir l'ordre de convergència de diferents mètodes de recerca d'una solució de l'equació f(x)=0, en classe (en grups menuts exposant a continuació les conclusions obtingudes) i a través un treball en equip.
- Treballar en aula d'informàtica elaborant programes per a aproximar una solució de l'equació f(x)=0, executar-los i valorar els resultats obtinguts.
Activitat 1: tenint en compte el Teorema de Bolzano,
Teorema -4: Per a tot interval [a,b] de nombres reals, i tota funció contínua f : [a,b]→R, si f(a)·f(b)<0, llavors existeix un nombre xc[a,b] tal que f(x)=0,
| si es compleix la premissa del teorema i prenent inicialment u=a & v=b, calculant w=(u+v)/2 i examinant el signe de f(w), estudiar quin nou interval hauríem de prendre per a seguir fitant la solució (mètode de la Bisecció). | 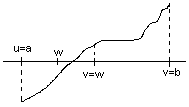 |
Pot trobar-se un model d'algorisme en http://www.uv.és/pla/Tutoria/mniq/algorit1.gif
Si reiterem el procés fins que la longitud de l'interval siga menor que una tolerància ε, de què dependrà, en general, el nombre de vegades que hàgem de reiterar-lo?
Activitat 2.
Problema 4: Si a=0, b=8, ε=0.25, quants passos seran necessaris com a màxim per a arribar a una solució aproximada amb aqueixa cota d'error? Obtenir una expressió general que ens done el nombre de passos en funció de a, b i ε.
Activitat 3 . Suposant a< b
& f(a)·f(b)<0 i prenent inicialment u=a & v=b,
obtenir l'equació de la recta
que passa pels punts (u,f(u)) & (v,f(v)) i calcular el
punt (w,0) que talla a l'eix d'abcises,
w = |
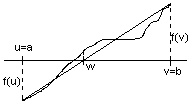 |
Pot experimentar-se gràficamente amb un "applet" en http://www.apropos-logic.com/nc/RegulaFalsiAlgorithm.html
Pot trobar-se un model d'algorisme en http://www.uv.és/pla/Tutoria/mniq/algorit2.gif
Activitat 4.
Problema 5: Aplicar el mètode de Regula-Falsi en la figura adjunta fins que la longitud de l'interval siga menor a la del segment indicat (ε):
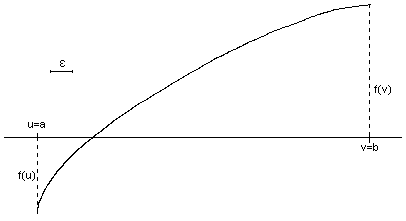
Activitat 5.
Problema 6 . Repetir el problema anterior en la figura adjunta modificant el mètode seguit de manera que quan dos valors intermedis w consecutius ens donen valors de f(w) amb el mateix signe, en comptes de tornar a traçar la recta fins al mateix punt que en el pas anterior, es trace fins a un punt amb la meitat de l'ordenada, segons es mostra en la figura menuda (mètode de Regula-Falsi modificat)


Pot experimentar-se gràficament amb un "applet" (adaptat per a Netscape 4.5) en http://www.uv.és/pla/java/Regulafa.html
Activitat 6 . Calculant per a un valor x els valors de la funció f(x) i de la seua derivada f '(x), obtenir l'equació de la recta tangent corresponent (recta que passa pel punt (x,f(x)) de pendent f '(x) ) i calcular el punt (v,0) que talla a l'eix d'abcises,
v = |
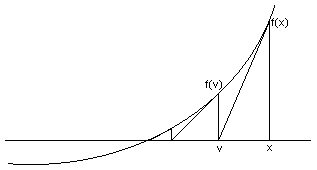 |
Pot trobar-se un model d'algorisme en http://www.uv.és/pla/Tutoria/mniq/algorit4.gif
Pot experimentar-se gràficament amb un "applet" (adaptat per a Netscape 4.5) en http://www.uv.és/pla/java/Newton.html
Activitat 7.
Problema 7: Aplicar el mètode de Newton a l'equació f(x)=2x/(1+x2) a partir del punt x=1/3½ (fer els càlculs sense aproximar). Interpretar el resultat a partir de la figura adjunta.
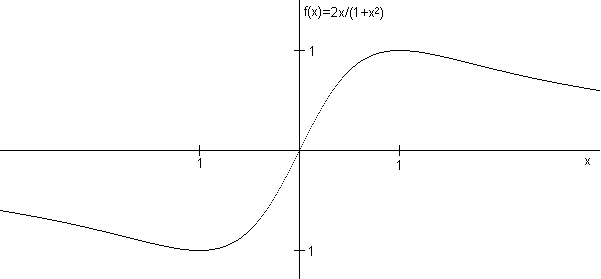
Activitat 8. Definint l'ordre de convergència
d'una successió per la
Definició 8:
Donats pcR+,
αcR i la
successió de nombres reals (xn)ncN tal que
α=lim n→∞ xn,
direm que aquesta successió té ordre de
convergència p si i
només si existeix un nombre real L≠0 tal que
& si p=1, llavors |L|<1.
Teorema -5: Per a tot interval [a,b] de nombres reals, tota funció real contínua i derivable fins a segon ordre en aquest interval, fcC2([a,b],R), i tot parell de nombres α,xc[a,b], existeix ξc[α,x] tal que
Teorema 16: Per a tot fcC2([x0,y0],R), x0,y0cR tals que f(x0)·f(y0)≠0 , si per a tot ncN,
xn+1 = xn - f(xn)(yn-xn)/(f(yn)-f(xn))
yn+1 = yn
& α = lim n→∞ xn
& per a tot xc[x0,i0], f "(x)≠0,
llavors existeix ηc[α,y0] tal que
lim n→∞ |xn+1-α|/|xn-α| = 1/(1+2f '(α)/(f "(η)(y0-α)))
Activitat 9.
Problema 8: Examinar la figura adjunta per a determinar quin és, en les condicions del Teorema 16, el signe de
f '(α)/(f "(η)(y0-α))
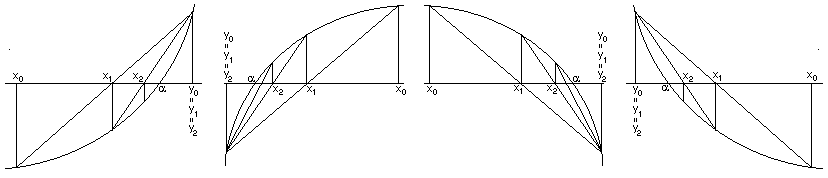
Activitat 10. Demostrar el
Teorema 17: Per a tota fcC2([x0,y0],R) amb x0,y0cR tals que f(x0)·f(y0)≠0 & per a tot xc[x0,y0], f "(x)≠0 , el mètode de Regula-Falsi té ordre de convergència 1.
Activitat 11. Aplicant el desenvolupament en sèrie de Taylor de f(x) fins al segon ordre, així com el desenvolupament en primer ordre de f '(x),
Teorema -6: Per a tot interval [a,b] de nombres reals, tota funció real contínua i derivable fins a segon ordre en aquest interval, fcC2([a,b],R), i tot parell de nombres α,xc[a,b], existeix ξc[α,x] tal que
f '(x) = f '(α) + f "(ξ)(x-α)
demostrar el
Teorema 17: Per a tot subconjunt A de R i tota fcC2(A,R), α,x0cA, si per a tot ncN,
xn+1 = xn - f(xn)/f '(xn) c A.
& α = lim n→∞ xn
& f(α)=0 & f '(α)≠0 (arrel simple)
& f "(α)≠0.
llavors el mètode de Newton té ordre de convergència 2.
Què podria passar si f "(α)=0?
Activitat 12 . Demostrar el
Teorema 18: Per a tot
subconjunt A de R i tota fcC2(A,R),
α,x0cA, si per a tot ncN,
xn+1 = xn
- f(xn)/f '(xn) c A
& α = lim n→∞ xn
& f(α)=0 & f '(α)=0 (arrel
múltiple)
llavors el mètode de Newton té ordre de
convergència 1.
Activitat 13 . Utilitzant
l'expressió
del desenvolupament en sèrie de Taylor fins a l'ordre m+1,
Teorema -7: Per a tot
interval [a,b] de nombres reals, tota funció real
contínua i derivable fins a ordre m+1 en aquest interval, fcCm+1([a,b],R),
i tot parell de nombres α,xc[a,b],
existeix ξc[α,x]
tal que
i recordant que
Teorema -8: Per a tot mcN, (m+1)! = (m+1) m!
demostrar el
Teorema 19: Per a tot subconjunt A de R i tota fcCm+1(A,R), α,x0cA, si per a tot ncN,
xn+1 = xn - m·f(xn)/f '(xn) c A (mètode de Newton modificat)
& α = lim n→∞ xn
& per a tot i=0,1,...m-1, f (i)(α)=0 & f (m)(α)≠0 (arrel de multiplicitat m)
& f (m+1)(α)≠0.
llavors la successió (xn)ncN té ordre de convergència 2.
Què podria passar si f (m+1)(α)=0?
| Activitat
14. Problema 9: Aplicar el mètode de Newton (modificat si escau) a l'equació f(x) = x3 = 0, representada en la figura adjunta. Quin podria ser el seu ordre de convergència? |
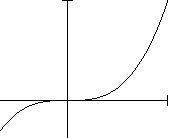 |
Treball 3 (per a la seua realització en equip):
Obtenir algebraicament les solucions de l'equació x2-5x+6=0 .
Aplicar el mètode de Newton para aproximar-se a una solució α a partir del valor inicial x0=1 fins a arribar a una distància menor a 0'1 d'aquesta solució.
Calcular
limxn→α (xn+1-α)/(xn-α)2 per a comprovar que la successió generada pel mètode de Newton a partir de x0=1 té ordre de convergència 2 .
Tema 3: Trobar una funció polinòmica que passe per un conjunt de punts:
Objectius:
- Demostrar l'existència i unicitat del polinomi interpolador de grau menor o igual que m que passa per m+1 punts d'abcises distintes.
- Trobar una fórmula que ens done directament l'expressió del polinomi interpolador.
- Trobar un mètode per a obtenir successivament punts interpolats a mesura que introduïm nous punts per a interpolar.
- Trobar un mètode que ens done successius
termes del polinomi interpolador.
- Trobar un mètode per a interpolar coneixent les ordenades d'un conjunt de punts i algunes derivades en els mateixos.
- Entendre els problemes de fiabilitat
de la interpolació, especialment si es realitza fora de
l'interval en el qual es tenen dades (extrapolació) o
s'utilitzen
polinomis d'un grau elevat.
- Deduir enunciats lògicament, treballant en la mesura d'allò possible en grups menuts per a exposar a continuació públicament la seua demostració.
- Aplicar algorismes per a resoldre problemes en grups menuts, exposant a continuació públicament la seua resolució.
- Treballar en aula d'informàtica elaborant programes per a interpolació i regressió lineal, executar-los i valorar els resultats obtinguts.
Activitat 1 . Tenint en compte la condició necessària i suficient perquè un sistema d'equacions lineals siga determinat, el valor del determinant de Vandermonde,
Teorema -9: |xki| = ∏ k>i (xk-xi)
i la
Definició 9: Direm que p(x) = ∑ i=0 m ai xi és un polinomi interpolador de grau menor o igual que m en els punts
{(xk,fk) / k=0,1...m} si i només si, per a tot k=0,1...m, p(xk)=fk ,
demostrar el
Teorema 20: Si per a tot i≠k, xi≠xk, llavors existeix un únic polinomi interpolador de grau menor o igual que m en els punts {(xk,fk) / k=0,1...m} .
Activitat 2 . Tenint en compte que
∑ i=0 m Ξi = Ξk + ∑ i≠k Ξi per a tot k=0,1...m, i que
∏ j≠i Ξkj = Ξkk·∏ j≠i & j≠k Ξkj per a tot i≠k.
demostrar el
| Teorema 21: Si per a tot i≠k, xi≠xk, llavors p(x) = ∑ i=0 m fi | ∏ j≠i (x-xj) ∏ j≠i (xi-xj) |
Activitat 3.
Problema 10: Donats els punts
| x k. |
1. |
2. |
4. |
5. |
| f k |
0. |
2. |
12. |
21. |
(suggeriment: a l'aplicar la fórmula, escriure primer cada denominador per a evitar errors)
Activitat 4 . Demostrar el
Teorema 22: Si per a tot i,j=0,1...m, si i≠k, llavors xi≠xk,
& si i+j≤m , llavors pi,j és el polinomi interpolador de grau menor o igual que j en {(xk,fk) / k=i,i+1...i+j},
llavors per a tot j=1...m, i=0,1...m-j,
| pi,j(x)
= |
(xi+j-x)pi,j-1
+ (x-xi)pi+1,j-1. xi+j - xi |
Activitat 5 . Tenint en compte que, amb els pi,j definits en el Teorema 22,
Teorema 23: per a tot i=0,1...m & per a tot xcR, pi,0(x) = f i
i
Teorema 24: p0,m és el polinomi interpolador de grau menor o igual que m en {(xk,fk) / k=0,1...m} ,
utililizar l'algorisme
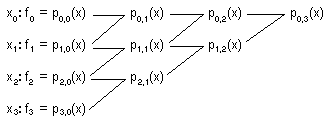 (mètode
de Neville)
(mètode
de Neville)per a resoldre el
Problema 11: Donats els punts
| x k |
1. |
2. |
4. |
| f k |
0. |
2. |
12. |
Afegir a continuació el punt (x3, f3) = (5, 21) i obtenir la nova interpolació per a x=3 .
Comparar el resultat obtingut amb el del problema 10.
Activitat 6 . D'acord amb la
Definició 10: Amb {(xk,fk) / k=0,1...m} tal que per a tot i,j=0,1...m, si i≠k, llavors xi≠xk, definirem les diferències dividides f[xi,xi+1,...xj] mitjançant| f[xi]
= |
fi | per a tot
i=0,1...m |
| f[xi,xi+1,xj]
= |
f[xi+1,...xj]
- f[xi,...xj-1] xj - xi |
per a tot i=0,1...m-1
, j=i+1,...m |
| f[x0] f[x1] f[x2] f[x3] |
> f[x0,x1] > f[x1,x2] > f[x2,x3] |
> f[x0,x1,x2] > f[x1,x2,x3] |
> f[x0,x1,x2,x3] |
| k. |
0. |
1. |
2. |
3. |
| x k |
1. |
2. |
4. |
5. |
| f k |
0. |
2. |
12. |
21. |
pm(x) = ∑j=0 m f[x0,...xj] ∏i=0 j-1 (x-xi)
és el polinomi interpolador de grau menor o igual que m en {(xk,fk) / k=0,1...m} (mètode de Newton)
Activitat 7 . Recordant que, d'acord amb la fórmula de Taylor
Teorema -10: pm(x) = ∑j=0 m [ f (j)(x0) / j! ] (x-x0)j és el polinomi de grau menor o igual que m que compleix les condicions pm(j)(x0)=f(j)(x0) per a j=0,1...m
així com que
Teorema -11: limx→xi (f(x)-f(xi))/(x-xi) = f '(xi)
prendrem
Definició 11: f[xi,xi+1,...xj] = f (j-i)(xi)/(j-i)! si xi=xi+1=...=xj i coneixem la derivada d'ordre j-i en el punt xi de la funció f a interpolar (naturalment, serà també fi=fi+1=...=fj),
amb el que podrem generalitzar el mètode de Newton repetint r vegades el punt (xi,fi) si coneixem les derivades fins a l'ordre r-1 en xi (interpolació d'Hermite).
Problema 13: Aplicar el mètode de Newton generalitzat a partir de les dades p(0)=1 , p'(0)=2 , p(1)=3. Comprovar que el resultat obtingut és el polinomi de grau igual o inferior a 2 que compleix aquestes condicions.
Activitat 8 . Assumint que l'error de la interpolació polinòmica de grau menor o igual que m ve donada per
Teorema -12: f(x)-pm(x) = [f (m+1)(ξ(x))/(m+1)!] ∏i=0 m (x-xi) tal que ξ(x)c[a,b] tal que per a tot i=0,1...m, xic[a,b]
Problema 14: Fitar el valor de f(3) suposant que
| x k |
1. |
2. |
4. |
5. |
| f(x k) |
0. |
2. |
12. |
21. |
Tema 4.
Obtenir una
solució aproximada de la integral definida d'una
funció, ∫ab f(x)dx :
Objectius:
- Obtenir uns pesos Wk independents de la funció f(x) tals que sumant el seu producte pels corresponents valors de la funció en determinats nodes xk, ∑ i=0 m Wk f(xk), proporcione la integral exacta per a polinomis fins a un cert grau, i una bona aproximació per a altres funcions.
- Aprendre a fitar l'error d'aquesta aproximació expressant-lo com el producte d'un factor C independent de la funció f(x) per la derivada d'un cert ordre r de la funció en algun punt ξ de l'interval d'integració [a,b] , Cf(r)(ξ).
- Estudiar el cas de nodes equidistants, xk=a+kh (Fórmula de Newton-Cotes).
- Aprendre a millorar l'aproximació augmentant el
nombre de nodes.
- Aprendre a millorar l'aproximació utilitzant valors de la derivada de la funció.
- Aprendre a millorar l'aproximació escollint de forma adequada els nodes (integració gaussiana).
- Aprendre a valorar comparativament diferents mètodes tenint en compte tant el seu màxim error d'aproximació com el seu cost de computació.
- Utilitzar el mètode de coeficients indeterminats per a obtenir tant els pesos Wk com el factor C de l'error, a partir de la integral exacta de potències simples i resolent en grups menuts els corresponents sistemes d'equacions per a exposar públicament a continuació els resultats obtinguts.
- Aplicar les fórmules obtingudes per a aproximar la integral de determinades funcions treballant en grups menuts i exposant públicament a continuació els resultats obtinguts.
- Treballar en aula d'informàtica elaborant programes per a l'aproximació d'integrals per diferents mètodes, valorant i comparant els resultats obtinguts.
Activitat 1. Tenint en compte la
Definició 14: Sent f:[a,b]→R una funció integrable, anomenarem integral numèrica polinòmica de f en els nodes xk tals que a≤x0<...<xm≤b a la integral en l'interval [a,b] del polinomi interpolador de grau menor o igual que m en els punts {(xk,f(xk)}k=0,1...m
i utilitzant l'expressió del polinomi interpolador proporcionada pel mètode de Lagrange, justificar l'existència d'uns pesos Wk independents de la funció f(x) amb els quals ∑ i=0 m Wk f(xk) siga la seua integral numèrica polinòmica.
Activitat 2. Tenint en compte que una integral numèrica polinòmica en m+1 nodes és igual a la integral exacta per a polinomis de grau menor o igual que m, trobar un sistema d'equacions per a l'obtenció dels pesos Wk i demostrar que si per a tot i≠k, x*i≠xk, aquest sistema d'equacions té solució única.
Activitat 3.
Deduir la fórmula de la integral numèrica polinòmica prenent com nodes els extrems de l'interval (Fórmula del Trapezi),
T=
Activitat 4.
Problema 15: Aplicar la Fórmula del Trapezi per a obtenir una aproximació a la integral de (1+x3)½ entre 0 i 10 (veure Figura en http://www.uv.es/pla/Tutoria/mniq/p15.gif).
Activitat 5. Tenint en compte
l'expressió de l'error de la interpolació
polinòmica de grau menor o igual que m donada pel Teorema -12
, així com que
Teorema -13: Per a
tota
funció integrable f:[a,b]→R, |∫a b f(x)dx|
≤ ∫a b |f(x)|dx .
Teorema -14: Per a tot
parell de funcions integrables f:[a,b]→R, g:[a,b]→R+,
existeix ξc[a,b]
tal
que
Teorema 25: El valor absolut de l'error de la integral numèrica polinòmica en m+1 nodes pot fitar-se pel producte de dos factors, un dels quals depèn únicament dels nodes, i l'altre depèn únicament de la derivada d'ordre m+1 en algun punt ξ de l'interval d'integració [a,b].
Activitat 6. Suposant que l'error d'un mètode d'integració aproximada siga de la forma
NOTA: en cas d'obtenir-se C=0 pot inferir-se que el mètode és exacte per a aquesta funció, i haurà de repetir-se el procés substituint r per r+1 .
Activitat 7.
Obtenir l'expressió de l'error per a la Fórmula del Trapezi,
εT =
Indicar per a quins polinomis serà exacta aquesta fórmula.
Activitat 8.
Problema 16: Fitar ∫0 10 (1+x3)½dx sabent que |f "(x)|<1'468 en aquest interval.
Activitat 9. Tenint en compte el
Teorema -15: ∫a b f(x) dx = ∫u-1(a) u-1(b) f(u(t)) u'dt
demostrar el
Teorema 26: En el cas de nodes equidistants x k=a+kh, amb k=0,1...m, h=(b-a)/m, demostrar que els pesos per al càlcul de la corresponent integral numèrica polinòmica (pesos de Newton-Cotes) tenen la forma Wk=hW'k(m), on W'k(m), que són els pesos corresponents al cas h=1, només depenen de k i de m (però no de a i de b ).
Pot utilitzar-se per a la demostració l'expressió dels pesos Wk obtinguda en l'Activitat 1, aplicant en la corresponent integral el canvi de variable x=a+th .
Activitat 10. Obtenir els pesos de Newton-Cotes per a m=2 i l'interval [0,2]. A partir dels mateixos, obtenir la fórmula general (Fórmula de Simpson) per a la integral numèrica polinòmica en els nodes {a, a+h, a+2h} = {a, (a+b)/2, b},
S =
Activitat 11.
Problema 17: Aproximar mitjançant la Fórmula de Simpson ∫-1 1 e x2 dx .
Activitat 12 . Tenint
en compte el
| Teorema -16: Per a tot fcC r(R→R),
xcC1(R→R),
|
dr f
dtr |
(x(t)) = ﴾dx/dt﴿r |
dr f
dxr |
(x) |
Teorema 27: Si l'expressió de l'error per a aproximar ∫0 m f(t)dt amb nodes equidistants i h=1 és
| ε' = C' | dr f dtr |
(ζ) per a algun ζc[0,m], |
| ε = C. | dr f dxr |
(ξ) per a algun ξc[a,b] amb C=hr+1 C' |
Activitat 13. Obtenir l'expressió de l'error per a la Fórmula de Simpson per a l'interval [0,2] (amb h=1), i a partir d'ella obtenir l'expressió general de l'error per a la Fórmula de Simpson per a l'interval [a,b] (amb h=(b-a)/2),
εS =
Indicar per a quins polinomis serà exacta aquesta fórmula.
Activitat 14.
Problema 18: Fitar l'error de la Fórmula de Simpson aplicada a ∫-1 1 e x2 dx . Valorar-lo.
Activitat 15. Tenint en compte la
Definició 15: Sent f:[a,b]→R una funció integrable, anomenarem integral numèrica composta de grau m en els mM+1 nodes {a+kh}k=0,1...mM , amb h=(b-a)/(mM), a.
demostrar el
Teorema 28: Per a tota funció integrable f:[a,b]→R , la seua integral numèrica composta de grau 2 en els 2M+1 nodes {a+kh}k=0,1...2M , amb h=(b-a)/(2M) (regla de Simpson), ve donada per
= [f(a) + f(b) + ∑i=1 M-1 2f(a+2ih) + ∑i=0 M-1 4f(s+(2i+1)h)](b-a)/(6M)
Activitat 16. Tenint en compte el
Teorema -17: Per a tota funció contínua f:[a,b]→R i tot conjunt de punts ξ ic[a,b], i=1...n, existeix ξc[a,b] tal que
Teorema 29: Per a tota fcC4([a,b],R), l'error de la regla de Simpson per aproximar ∫a b f(x)dx ve donat per
Activitat 17.
Problema 19: Quin increment h hauríem de prendre per a obtenir una aproximació a ∫-1 1 e x2 dx amb un error menor a 0'01 mitjançant la regla de Simpson?
Activitat 18. Calcular els
pesos adequats perquè W'0 f(0)+W'1
f(1)+W'2 f '(0)+W'3
f '(1) ens done el valor exacte de
∫0 1 f(t)dt per a polinomis fins
al
tercer grau. A partir d'aquests pesos, i tenint en compte el
Teorema -18: Per a tot
fcC r(R→R),
xcC1(R→R),
df/dt = (df/dx)·(dx/dt) ,
obtenir la fórmula general (Fórmula
del Trapezi Corregida) que resulta de substituir la integral ∫a
b f(x)dx per la integral del polinomi interpolador d'Hermite
per
al qual
coincideixen els valors de la funció i de la seua primera
derivada
en els extrems de l'interval,
TC=
Comparar amb la fórmula obtinguda en l'Activitat 3 i justificar
per què es diu Fórmula del Trapezi Corregida. En quin
cas ambdues fórmules coincidiran?
Activitat 19. Obtenir
l'expressió
de l'error per a la Fórmula del Trapezi
Corregida per a
l'interval [0,1] (amb h=1), i a partir d'ella obtenir
l'expressió
general de l'error per a la Fórmula del Trapezi Corregida per a
l'interval [a,b]
(amb h=b-a),
εTC =
Indicar per a quins polinomis serà exacta aquesta
fórmula.
Activitat 20.
Problema 20:
Fitar ∫0 10 (1+x3)½dx
sabent que |f (4)(x)|<10 en aquest
interval (veure Figura en http://www.uv.es/pla/Tutoria/mniq/p15.gif).
Activitat 21. Demostrar el
Teorema 30: Per a tota
fcC4([a,b],R),
Activitat 22. Tenint en compte que el cost computacional del càlcul numèric aproximat d'una integral pot amidar-se pel nombre de vegades que s'avalua la funció f(x) o la seua derivada f '(x), comparar el cost computacional de la regla de Simpson i la regla del Trapezi Corregida amb el mateix valor de M. Quin seria el cost computacional de la regla de Simpson amb M=11? Per a quin valor de M la regla del Trapezi Corregida tindria el mateix cost computacional? Comparar l'estimació dels errors d'ambdues regles amb el mateix cost computacional.
Activitat 23.
Problema 21: Quin increment h hauríem de prendre per a obtenir una aproximació a ∫-1 1 e x2 dx amb un error menor a 0'01 mitjançant la regla del Trapezi Corregida? Comparar el seu cost computacional amb el del Problema 19 (Activitat 17).
En quins casos serà preferible utilitzar la regla del Trapezi Corregida?
Activitat 24. Calcular els
pesos W'0 i W'1 i
el valor de c per als quals W'0
f(-c) + W'1 f(c) dóna el valor exacte
de
∫-1 1 f(t)dt per a polinomis
fins al segon grau. Comprovar que {-c, c} són les arrels del polinomi de Legendre
de 2º grau, P2(t)=(3t2-1)/2
, que compleix les condicions d'ortogonalitat
∫-1 1 P2(t)P1(t)dt
= 0.
∫-1 1 P2(t)P0(t)dt
= 0.
amb P0(t)=1 i
P1(t)=t
polinomis de Legendre que compleixen al seu torn
∫-1 1 P1(t)P0(t)dt
= 0.
Activitat 25. Obtenir
l'expressió
de l'error de la integral numèrica
polinòmica de ∫-1 1 f(t)dt
en les arrels del polinomi de Legendre de 2º grau.
Indicar per a quins polinomis serà exacte aquest
mètode.
Activitat 26. Obtenir una
fórmula general per a la integració de ∫ab
f(x)dx realitzant el canvi x=(a+b)/2 + (b-a)t/2 i utilitzant la
integral
numèrica polinòmica de ∫-1 1
f(t)dt en les arrels del polinomi de Legendre de
2º grau,
L2 =
amb un error
εL2 =
Activitat 27.
Problema 22:
Aproximar, utilitzant la fórmula derivada de la
integració numèrica polinòmica en
les arrels del polinomi de Legendre de 2º grau,
a) ∫-1 1
e x2 dx
b) ∫0 10 (1+x3)½dx
Fitar els corresponents errors.
Activitat 28. Demostrar el
Teorema 31: Per a tota
fcC4([a,b],R),
Treball 4 (per a la seua realització en equip):
Obtenir els coeficients W0, W1, W2 i W3 que fan que