DEL PARADIGMA MECANICISTA DE LA CIENCIA AL PARADIGMA SISTÉMICO
Lorenzo Ferrer Figueras
UNIVERSITAT DE VALÈNCIA / AJUNTAMENT DE VALÈNCIA
1997

GUÍA DIDÁCTICA
Rafael Pla López
Entre Ríos (Argentina)
octubre de 2008

Objetivos:
Específicos:
- Superar las limitaciones del paradigma mecanicista (capítulos 1, 2 y 3)
- Seguir la formación del paradigma sistémico (capítulos 3 y 4)
- Aplicar el paradigma sistémico a los problemas de hoy (capítulos 5 y 7)
- Vislumbrar el futuro de la Ciencia de Sistemas (capítulo 6)
- Estudiar la formación de sistemas y
suprasistemas en
Latinoamérica (introducción)
Genéricos:
- Trabajar en equipo.
- Exponer públicamente.
- Respetar y criticar las ideas expuestas.
- Comprender e interactuar con el entorno social.
Metodología:
- Realizar actividades en grupos reducidos.
- Exponer y debatir en gran grupo los resultados obtenidos.
1. Superar las limitaciones del paradigma mecanicista:
Actividad 1.1. Para trabajar las antinomias racional-irracional, logos-mito, cada uno deberá formular una afirmación razonada, y a continuación identificar en un grupo reducido las premisas incuestionadas en las que se fundamenta. Atender a que no se trata de debatir las afirmaciones ni las premisas, sino únicamente de identificarlas. Una vez realizada dicha tarea, cada uno expondrá públicamente su afirmación razonada, y otra persona previamente acordada en el grupo expondrá las premisas incuestionadas de la misma. A continuación se debatirá si existen otras premisas subyacentes que no se hubieran explicitado.
Actividad 1.2. El método científico tradicional se asocia a la reducción del problema a estudiar a determinados rasgos y a la posibilidad de repetir las experiencias a realizar sobre el mismo, y así de refutar suposiciones al respecto. El ideal del paradigma mecanicista sería asimismo que los fenómenos complejos pudieran siempre explicarse mediante fenómenos simples (Ockham): Así, los fenómenos sociológicos se reducirían a fenómenos psicológicos, éstos a fenómenos biológicos, éstos a fenómenos químicos y éstos a fenómenos físicos. Si en determinados casos la reducción no fuera posible deberíamos hablar de emergencia (de la física a la química, de ésta a la biología, de ésta a la psicología, de ésta a la sociología).
Analizar si en los siguientes fenómenos se da reducción o emergencia:
a) El cloruro sódico como combinación de iones de sodio Na+ y de cloro Cl -
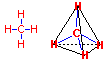 b) La estructura del
metano CH4
b) La estructura del
metano CH4d) El metabolismo
e) El camuflaje del camaleón
f) La fatiga muscular
g) El "jet lag"
h) Una avalancha humana ante un incendio
i) La respuesta a los ciclones en Haití, Cuba y EE.UU.
¿Qué diferencia hay entre el grafito y el diamante?
 Actividad 1.3.
Estudiar en qué casos el conocimiento de un todo se reduce a
la
suma del conocimiento de sus partes (Descartes).
¿Qué "todo"
podría obtenerse a partir de la
"suma" de las siguientes partes?:
Actividad 1.3.
Estudiar en qué casos el conocimiento de un todo se reduce a
la
suma del conocimiento de sus partes (Descartes).
¿Qué "todo"
podría obtenerse a partir de la
"suma" de las siguientes partes?: Actividad 1.4. La metodología de Popper estipula que lo propio de una teoría científica es ser falsable por la experiencia, de modo que si experimentos repetidos la contradicen la teoría debe ser abandonada. Kuhn replica que si se encuentra tal contradicción revela una "anomalía", pero no conlleva el abandono inmediato de la teoría, sino que la práctica de la Ciencia "Normal" supone un esfuerzo por encajar experiencias y teoría interpretando o reinterpretando los resultados experimentales de acuerdo con dicha teoría, la cual entraría en crisis sólo cuando menudearan las anomalías y fracasaran repetidamente los intentos de resolverlas; pero la teoría en cuestión no se abandonaría hasta que surgiera una teoría mejor que se impusiera a través de una Revolución Científica o cambio de "paradigma" propio de lo que Kuhn llama Ciencia "Extraordinaria".
La relación entre teoría y experiencia puede entenderse también como un proceso de Aprendizaje a través del cuál una teoría resulta reforzada positiva o negativamente en función de los resultados experimentales.
Debatir en qué medida una teoría científica se contrasta con experiencias aisladas o con un sistema de experiencias emanadas de una realidad compleja.
Actividad 1.5. Según Comte, a lo largo de la historia el pensamiento pasaría de la fase "teológica" (fetichismo, causas sobrenaturales...) a la "metafísica" (estudio de propiedades) y de ésta a la "positiva" (leyes que gobiernan los fenónemos). Este proceso se produciría paulatinamente respecto a distintos aspectos de la realidad, de menor a mayor "complejidad", generándose así sucesivamente distintas disciplinas científicas: Física, Química, Biología, Sociología... Según Ken Wilber, una disciplina "superior" que estudia realidades más complejas no puede violar las leyes de una disciplina "inferior", pero dichas realidades no pueden explicarse exclusivamente por dichas leyes.
Ahora bien, habiendo sido la Física la primera disciplina científica en desarrollarse, el método científico tradicional se elaboró de acuerdo con sus características, como ciencia que estudia propiedades comunes a todos los procesos materiales. Pero a medida que se estudian realidades más complejas la "reducción" y la "repetición" se hacen más difíciles y se hace más necesario trabajar con totalidades en la que lo específico adquiere mayor relevancia.
Intentar describir experimentos repetibles en Física, en Química, en Biología y en Ciencias Sociales. Analizar también en qué medida las leyes son "generales" o "especiales" en unas y otras ciencias.
¿Por qué el diseño de golpe de Estado (protestas callejeras seguidas de un levantamiento militar) que triunfó en Chile en 1973 fracasó en Venezuela en 2002? ¿En qué medida el conocimiento de la historia puede prevenir su repetición?
Activitat 1.6. El método "analítico", "reduccionista", propio del paradigma mecanicista, requiere "aislar" una determinada porción de la realidad. Ahora bien, según el Segundo Principio de la Termodinámica, un sistema "aislado", cerrado, no puede aumentar su contenido de información, su complejidad, sino que tiende a degradarse, a desorganizarse, a aumentar su "entropía". Por ello, aquellos procesos materiales en los que es esencial el aumento de su información, y el desarrollo de su complejidad no pueden ser sistemas "aislados" ni pueden ser explicados plenamente con una metodología "reduccionista", sino que es imprescindible tener en cuenta las interacciones con su entorno: de acuerdo con Ilya Prigogine, en un Sistema Abierto el incremento de entropía viene dado por dS=diS+deS, donde diS, que mide la entropía producida en el sistema, no puede ser negativa (será positiva siempre que se den procesos irreversibles), pero deS, que mide la entropía transmitida desde su entorno, puede ser positiva o negativa; de este modo, si la disminución de entropía por deS<0 supera el aumento de entropía por diS>0, puede darse dS<0, con lo cual la entropía del Sistema Abierto disminuiría, aumentando su organización con la información acumulada en el mismo.
Analizar si los siguientes procesos materiales pueden explicarse con una metodología "reduccionista" como sistemas aislados:
a) La combustión en el motor de un submarino
b) El ciclo del agua en el planeta Tierra
c) El choque de protones en el LHC del CERN
d) El crecimiento de una planta
e) La descomposición de un cadáver
f) El aprendizaje de una asignatura
g) La revolución industrial
2. Seguir la formación del paradigma sistémico:
Actividad 2.1. La aparición y desarrollo del método científico tradicional a través de las distintas disciplinas científicas, con raíces en el pensamiento griego y que tiene su eclosión en la Revolución Científica del siglo XVII, coexiste con rasgos de pensamiento pre-sistémico:
Pero ello se produce en el
marco de una
hegemonía creciente de lo que llamamos método
científico
tradicional (basado en el reduccionismo, la repetición y la
refutación) plasmado en distintas disciplinas
científicas
alrededor del paradigma mecanicista. Este paradigma entrará
en
crisis en la primera mitad del siglo XX, a raíz de la
revolución científica que lleva de la
Mecánica
Clásica (sobre la cuál se había
construido dicho
paradigma) a la Mecánica Relativista, Cuántica y
No
Lineal. En la segunda mitad del siglo XX emergerá el nuevo
Paradigma Sistémico integrando las aportaciones de la
Investigación Operativa, la Teoría General de
Sistemas,
la Cibernética, la Teoría de la
Información y las
teorías de catástrofes y fractales.
Discutir, a la luz de la antinomia repetición-evolución,
a) en qué medida es posible encajar en el paradigma mecanicista las nuevas disciplinas que se van desarrollando entre los siglos XIX y XX, como la Biología, la Psicología o la Economía;
b) en qué medida es razonable sostener que como las cosas han ocurrido de determinada manera en el pasado, continuarán ocurriendo así en el futuro;
c) si es suficiente conocer el mundo, o hay que cambiarlo.
Actividad 2.2. Para la Gestión de problemas reales en la vida social (en lo que originalmente se llamó "Ciencia del Management") hay que precisar los objetivos a conseguir, considerar las distintas decisiones a tomar y las actividades a realizar, evaluar las desviaciones entre los resultados obtenidos y los objetivos perseguidos e introducir las consiguientes correcciones en las decisiones. Pero para realizarlo de modo eficiente (en lo que se ha llamado "Investigación Operativa") se diseña un Modelo del problema real y se aplican a dicho Modelo las técnicas reduccionistas y de repetición de experimentos propias del método científico tradicional. Puede comenzarse con un Modelo sencillo y posteriormente hacerlo progresivamente más complejo introduciendo nuevas variables y relaciones para adaptarse al problema real a resolver.
Por ejemplo, para resolver el problema del suministro de agua a un conjunto de edificios haciendo mínima la longitud total de las tuberías, comenzar resolviendo el problema en un modelo sencillo con tres edificios A, B y C situados en los vértices de un triángulo equilátero (el agua debe partir de un punto inicial de suministro exterior al triángulo y volver al mismo para su posterior depuración).
Actividad 2.3. El desarrollo de la Biología requiere un modelo de "complejidad organizada" con una jerarquía de niveles, en los que el nivel más complejo tiene propiedades "emergentes" que no se dan en el nivel inferior. La "Teoría General de Sistemas" (1947) de Bertalanffy aplicará dicho modelo a todo tipo de globalidades complejas ("organismos").
Escoger un organismo cualquiera, definir sus distintos niveles de organización y describir propiedades emergentes de los mismos.
Actividad 2.4. El desarrollo de un organismo requiere que sea un Sistema Abierto que incremente su información interaccionando con su entorno, de modo que sus niveles jerárquicamente superiores controlen a los inferiores en función de los objetivos del organismo. De este modo, al mismo tiempo que los niveles superiores deben cumplir las leyes generales de los inferiores (como las leyes de la Física o de la Química), la manera como se implemente la aplicación de estas leyes en los niveles inferiores (por ejemplo, los procesos físicos o las reacciones químicas específicas que ocurran) depende de las propiedades emergentes de los niveles superiores. Estos procesos se dan tanto en organismos biológicos como en máquinas artificiales, tal como explica Norbert Wiener en "Cibernética o control y comunicación en el animal y la máquina" (1948) a través de procesos de retroalimentación en los que la información sobre los resultados de las acciones del sistema repercute en las acciones posteriores del mismo.
Analizar, en el organismo escogido en la actividad anterior, cuáles son los objetivos del organismo y de qué modo la persecución de los mismos condiciona la actividad de sus niveles inferiores.
Actividad 2.5. Shannon y Weaver desarrollan una "Teoría Matemática de la Comunicación" (1949) en la que calculan la cantidad de información necesaria para fijar el estado de un Sistema partiendo de una previa distribución de probabilidades de sus posibles valores, dada por su entropía S=-∑ i pi·log(pi). Para aproximarnos al modo de medir la cantidad de información, simplificaremos suponiendo que las distintas opciones tienen la misma probabilidad inicial.
A tal efecto, resolver el siguiente problema: dadas 9 monedas aparentemente idénticas, pero una de las cuáles (falsa) es más pesada, determinar cuál es ésta con 2 pesadas de una balanza. Para ello, en grupos pequeños, en cada grupo un miembro hará de "balanza" extendiendo ambas manos con la palma hacia arriba y decidiendo mentalmente cuál sería la moneda falsa, mientras que los demás intentarán averiguar cuál es ésta poniendo una o más monedas en ambas manos.
Una vez resuelto el problema, será fácil deducir cuántas pesadas harían falta para determinar con seguridad una moneda falsa entre 27.
En el ejercicio anterior, la unidad de información es la pesada, que permite escoger entre tres opciones (>, <, =). Si el problema se intentara dilucidar con preguntas binarias, de SI o NO, la unidad de información sería un bit. ¿Entre cuántas opciones equiprobables se podría escoger con n bits? ¿Si tenemos que escoger entre W opciones, cuántos bits de información necesitaremos para hacerlo?
Podemos demostrar fácilmente que esta fórmula, establecida por Hartley, se obtiene como caso particular en el caso de equiprobabilidad de la fórmula de Shannon anteriormente expuesta.
Actividad 2.6. Hasta mediados del siglo XX, se presuponía que la imposibilidad de predecir el futuro de un Sistema provenía de su carácter no determinista, como ocurría en la Mecánica Cuántica. Pero en la segunda mitad del siglo emerge la dificultad de predecir también el futuro de sistemas deterministas. Pasa a primer plano el viejo proverbio sobre la mariposa cuyo aletear en París podía provocar un huracán en Brasil: cuando la evolución de un Sistema es muy sensible a las condiciones iniciales,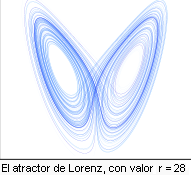 una
pequeña variación de éstas puede
provocar una gran
diferencia en el resultado final, noción que se desarrolla
en la
Teoría de las
Catástrofes
de René Thom (1972). Si el Paradigma Mecanicista
había
trabajado fundamentalmente con procesos lineales, en los que el efecto
era proporcional a la causa, los Sistemas No Lineales siguen
frecuentemente trayectorias complejas o caóticas.
En determinados
casos, no obstante, su evolución genera estructuras
emergentes a
través de un proceso de autoorganización.
Pero frecuentemente no tienden a estados simples, constantes o
periódicos, sino a lo que se llaman atractores extraños,
como el Atractor
de
Lorenz (1963) generado cuando las derivadas de las
coordenadas
(x,y,z) valen respectivamente x'=10(y-x), y'=x(r-z)-y, z'=xy-8z/3 con
valores de r suficientemente grandes.
una
pequeña variación de éstas puede
provocar una gran
diferencia en el resultado final, noción que se desarrolla
en la
Teoría de las
Catástrofes
de René Thom (1972). Si el Paradigma Mecanicista
había
trabajado fundamentalmente con procesos lineales, en los que el efecto
era proporcional a la causa, los Sistemas No Lineales siguen
frecuentemente trayectorias complejas o caóticas.
En determinados
casos, no obstante, su evolución genera estructuras
emergentes a
través de un proceso de autoorganización.
Pero frecuentemente no tienden a estados simples, constantes o
periódicos, sino a lo que se llaman atractores extraños,
como el Atractor
de
Lorenz (1963) generado cuando las derivadas de las
coordenadas
(x,y,z) valen respectivamente x'=10(y-x), y'=x(r-z)-y, z'=xy-8z/3 con
valores de r suficientemente grandes. 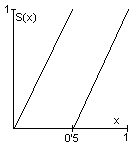 Los atractores
extraños
suelen ser casos particulares de fractales,
objetos de dimensiones fraccionarias
Los atractores
extraños
suelen ser casos particulares de fractales,
objetos de dimensiones fraccionarias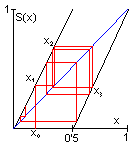 que tienen la
propiedad de
autosimilaridad, en los que su forma genérica se repite a
distintas escalas.
que tienen la
propiedad de
autosimilaridad, en los que su forma genérica se repite a
distintas escalas.
Podemos generar de forma sencilla un Sistema Caótico aplicando sucesivamente el operador Shift definido por S(x)=2x si 0≤x<0'5, S(x)=2x-1 si 0'5≤x<1, según se muestra en la figura adjunta a la izquierda. Los sucesivos valores de x pueden obtenerse gráficamente haciendo "rebotar" los trazos horizontales en la diagonal, como se indica en la figura adjunta a la derecha. También pueden obtenerse en sistema de numeración binario desplazando los "bits" (0s y 1s) un lugar a la izquierda y descartando la parte entera si aparece. Observar lo que ocurre si experimentamos con el operador Shift a partir de valores iniciales distintos pero muy próximos.
3. Aplicar el paradigma sistémico a los problemas de hoy:
Actividad 3.1. Para formular un problema y resolverlo desde el paradigma sistémico, debemos comenzar detectando los elementos o "síntomas" del mismo, y después establecer sus interrelaciones (sin predeterminar una relación causa-efecto apriorística, como incitaba a hacer el paradigma mecanicista), a partir de las cuáles podremos construir un Modelo y "validarlo" experimentalmente o estudiando los datos previamente disponibles. Las discrepancias que encontremos deberán "retroalimentarnos" modificando el modelo para superarlas. Repetiremos este proceso hasta obtener una aproximación aceptable a los datos de la realidad. Sólo después de disponer de un Modelo correctamente validado podremos determinar sobre qué factores podemos y debemos intervenir para conseguir los objetivos perseguidos. Establecer, utilizando la técnica de "brain storming", un primer Modelo sobre el ciclo urbano del agua en pequeños municipios, detectando los elementos a considerar y avanzando hipótesis sobre sus interrelaciones (no se trata de construir un modelo desarrollado a partir de todo lo previamente estudiado en el curso, sino de realizar un esbozo uniendo todas las ideas que formulen sin cortapisas los asistentes, incluyendo las que hubieran podido ser previamente descartadas). ¿Qué debería hacerse posteriormente con dicho modelo?
Actividad 3.2. Si no se tiene en cuenta el conjunto de las interrelaciones/decisores en un Sistema complejo, una actuación focalizada únicamente sobre un componente del mismo, como reacción a una situación generada a corto plazo y aplicando el paradigma mecanicista (aislando una parte del problema) puede tener efectos contraproducentes a medio o largo plazo. Poner ejemplos sobre casos en los que el "remedio" puede ser peor que la "enfermedad".
Actividad 3.3. Precisamente para evitar que ello ocurra es necesario recurrir al enfoque sistémico, teniendo en cuenta la globalidad de las interrelaciones/decisores, que el éxito de un miembro de un Sistema complejo interrelacionado puede depender del éxito de todos los demás (en "una asociación en que el libre desarrollo de cada uno condicione el libre desarrollo de todos") y que es necesario considerar las consecuencias no sólo a corto plazo sino también a medio y largo plazo. Reflexionar colectivamente sobre cómo podríamos actuar para evitar los efectos "perversos" de la aplicación del paradigma mecanicista en los casos enunciados en la actividad anterior.
Actividad 3.4. Segun Miller (1978), los Sistemas Vivientes de diferentes niveles (células, órganos, organismos, grupos, organizaciones, sociedades y Sistemas Supranacionales) poseen un Suprasistema en su caso y 19 Subsistemas críticos que transfieren Materia, Energía e Información (reproductor, frontera), Materia y Energía (ingestor, distribuidor, conversor, productor, almacén, expulsor, sostén, motor) o Información (transductor de entrada, transductor de salida, transductor interior, canal y red, decodificador, asociador, memoria, decisor, codificador), y sufren un proceso a través del cuál nacen, se mantienen integrados persiguiendo sus objetivos a través de interacciones con su entorno, sufren "patologías" con desajustes entre sus Subsistemas, eventualmente se reproducen y finalmente entran en decadencia y terminan cuando no pueden ajustar sus variables esenciales o no pueden mantener la cohesión entre sus subsistemas. Definir un Sistema Social (un Sistema Viviente de alguno de los 4 niveles superiores) en el cuál se puedan identificar los 19 Subsistemas críticos.
Actividad 3.5. A través de isomorfismos (correspondencias entre los elementos y sus relaciones) entre los Sistemas Vivientes de distintos niveles, estudiados por distintas "disciplinas" científicas, se puede intentar aplicar "inductivamente" Modelos validados en niveles inferiores para cubrir huecos ("gaps") en niveles superiores. Formular isomorfismos entre problemas que aparecen en el nivel de Sistemas Supranacionales (por ejemplo, la crisis financiera global) y problemas de niveles inferiores. Indicar cómo podría utilizarse información sobre la resolución de problemas en tales niveles inferiores (estudiados por una o más disciplinas) para abordar el problema en el nivel superior, y qué equipos interdisciplinarios convendría formar para ello.
Actividad 3.6. A partir de un Modelo genérico validado para Sistemas Vivientes de todos los niveles, puede especificarse y aplicarse "deductivamente" a distintos niveles mediante distintos Modelos que serán isomorfos entre sí. Discutir en qué medida el pensamiento sistémico general puede contribuir al desarrollo de las distintas "disciplinas" científicas especializadas.
4. Vislumbrar el futuro de la Ciencia de Sistemas:
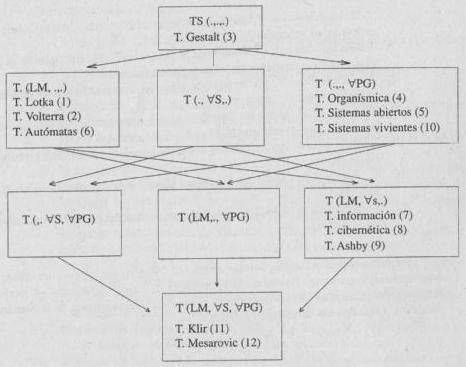 Actividad 4.1.
De los 40 a los 80 la Ciencia de Sistemas se orientaba a la
construcción de una Teoría General de Sistemas que
utilizando un lenguaje matemático (LM) abordara el estudio de
todos los problemas globales (
Actividad 4.1.
De los 40 a los 80 la Ciencia de Sistemas se orientaba a la
construcción de una Teoría General de Sistemas que
utilizando un lenguaje matemático (LM) abordara el estudio de
todos los problemas globales ( PG) en todos los Sistemas (
PG) en todos los Sistemas ( S),
camino en el que se desarrollan una serie de Teorías presentadas
jerárquicamente en la figura adjunta. Tal Teoría General
de Sistemas incorpora conceptos procedentes de las Ciencias
Biológicas y de las Ciencias Sociales (y también de las
Ciencias de la Computación), y sirve asimismo de "puente" para
trasladar tales conceptos de unas a otras.
S),
camino en el que se desarrollan una serie de Teorías presentadas
jerárquicamente en la figura adjunta. Tal Teoría General
de Sistemas incorpora conceptos procedentes de las Ciencias
Biológicas y de las Ciencias Sociales (y también de las
Ciencias de la Computación), y sirve asimismo de "puente" para
trasladar tales conceptos de unas a otras.
Encontrar conceptos procedentes de las Ciencias Biológicas o de las Ciencias Sociales (o de las Ciencias de la Computación) y que se hayan "trasladado" a las otras.
Actividad 4.2. A partir de los 80 comienza un proceso de formación de científicos de diversas "disciplinas" en el pensamiento sistémico, que llegan así a combinar una preparación como "especialistas" y como "generalistas", y aplicar nociones sistémicas en su posterior investigación "disciplinaria", nociones que van impregnando el desarrollo de distintas "disciplinas", tanto las que estudian sistemas biológicos y sociales como las que intentan desentrañar la estructura física de la materia. Por su parte, esas ciencias "particulares" ya con "sabor sistémico" generan aportaciones para nuevas síntesis generalistas que desarrollen la Teoría General de Sistemas.
Buscar conceptos "sistémicos" en la formación "disciplinaria" recibida por los distintos asistentes al curso.
Actividad 4.3. En las últimas décadas del siglo XX se generaliza el uso de ordenadores como instrumento para la investigación científica, y adquieren un nuevo impulso las matemáticas "discretas" orientadas al cálculo con ordenadores y la simulación de Modelos por ordenador. Se desarrolla Internet como una red global de comunicación mundial. La noción de autoorganización, apoyada en la cooperación de distintos sistemas, adquiere nueva relevancia para estudiar la emergencia a partir de situaciones caóticas (como la que ha conducido a la crisis financiera global de 2008).
Estudiar procesos de autoorganización en sistemas de diferente naturaleza, y analizar en qué medida pueden ayudar a resolver los problemas con los que se encuentran dichos sistemas para su supervivencia.
5. Estudiar la formación de sistemas y suprasistemas en Latinoamérica:
Actividad 5.1. Realizar un cuadro o cuadros de los Sistemas-Estados en el territorio de la actual Latinoamérica y sus distintos componentes étnicos a través de su historia.
Actividad 5.2. Estudiar los distintos Suprasistemas supranacionales proyectados, existentes o en formación en Latinoamérica (la Comunidad Andina, el Mercosur, el ALCA, el ALBA...). Intentar identificar en ellos los distintos Subsistemas críticos característicos de los Sistemas Vivientes.
Actividad 5.3. Estudiar las interrelaciones entre Sistemas-Estados en Latinoamérica y sus subsistemas territoriales y los procesos de integración y desintegración en los mismos. Estudiar en particular los casos de Argentina y de Bolivia.
Discutir, a la luz de la antinomia repetición-evolución,
a) en qué medida es posible encajar en el paradigma mecanicista las nuevas disciplinas que se van desarrollando entre los siglos XIX y XX, como la Biología, la Psicología o la Economía;
b) en qué medida es razonable sostener que como las cosas han ocurrido de determinada manera en el pasado, continuarán ocurriendo así en el futuro;
c) si es suficiente conocer el mundo, o hay que cambiarlo.
Actividad 2.2. Para la Gestión de problemas reales en la vida social (en lo que originalmente se llamó "Ciencia del Management") hay que precisar los objetivos a conseguir, considerar las distintas decisiones a tomar y las actividades a realizar, evaluar las desviaciones entre los resultados obtenidos y los objetivos perseguidos e introducir las consiguientes correcciones en las decisiones. Pero para realizarlo de modo eficiente (en lo que se ha llamado "Investigación Operativa") se diseña un Modelo del problema real y se aplican a dicho Modelo las técnicas reduccionistas y de repetición de experimentos propias del método científico tradicional. Puede comenzarse con un Modelo sencillo y posteriormente hacerlo progresivamente más complejo introduciendo nuevas variables y relaciones para adaptarse al problema real a resolver.
Por ejemplo, para resolver el problema del suministro de agua a un conjunto de edificios haciendo mínima la longitud total de las tuberías, comenzar resolviendo el problema en un modelo sencillo con tres edificios A, B y C situados en los vértices de un triángulo equilátero (el agua debe partir de un punto inicial de suministro exterior al triángulo y volver al mismo para su posterior depuración).
Actividad 2.3. El desarrollo de la Biología requiere un modelo de "complejidad organizada" con una jerarquía de niveles, en los que el nivel más complejo tiene propiedades "emergentes" que no se dan en el nivel inferior. La "Teoría General de Sistemas" (1947) de Bertalanffy aplicará dicho modelo a todo tipo de globalidades complejas ("organismos").
Escoger un organismo cualquiera, definir sus distintos niveles de organización y describir propiedades emergentes de los mismos.
Actividad 2.4. El desarrollo de un organismo requiere que sea un Sistema Abierto que incremente su información interaccionando con su entorno, de modo que sus niveles jerárquicamente superiores controlen a los inferiores en función de los objetivos del organismo. De este modo, al mismo tiempo que los niveles superiores deben cumplir las leyes generales de los inferiores (como las leyes de la Física o de la Química), la manera como se implemente la aplicación de estas leyes en los niveles inferiores (por ejemplo, los procesos físicos o las reacciones químicas específicas que ocurran) depende de las propiedades emergentes de los niveles superiores. Estos procesos se dan tanto en organismos biológicos como en máquinas artificiales, tal como explica Norbert Wiener en "Cibernética o control y comunicación en el animal y la máquina" (1948) a través de procesos de retroalimentación en los que la información sobre los resultados de las acciones del sistema repercute en las acciones posteriores del mismo.
Analizar, en el organismo escogido en la actividad anterior, cuáles son los objetivos del organismo y de qué modo la persecución de los mismos condiciona la actividad de sus niveles inferiores.
Actividad 2.5. Shannon y Weaver desarrollan una "Teoría Matemática de la Comunicación" (1949) en la que calculan la cantidad de información necesaria para fijar el estado de un Sistema partiendo de una previa distribución de probabilidades de sus posibles valores, dada por su entropía S=-∑ i pi·log(pi). Para aproximarnos al modo de medir la cantidad de información, simplificaremos suponiendo que las distintas opciones tienen la misma probabilidad inicial.
A tal efecto, resolver el siguiente problema: dadas 9 monedas aparentemente idénticas, pero una de las cuáles (falsa) es más pesada, determinar cuál es ésta con 2 pesadas de una balanza. Para ello, en grupos pequeños, en cada grupo un miembro hará de "balanza" extendiendo ambas manos con la palma hacia arriba y decidiendo mentalmente cuál sería la moneda falsa, mientras que los demás intentarán averiguar cuál es ésta poniendo una o más monedas en ambas manos.
Una vez resuelto el problema, será fácil deducir cuántas pesadas harían falta para determinar con seguridad una moneda falsa entre 27.
En el ejercicio anterior, la unidad de información es la pesada, que permite escoger entre tres opciones (>, <, =). Si el problema se intentara dilucidar con preguntas binarias, de SI o NO, la unidad de información sería un bit. ¿Entre cuántas opciones equiprobables se podría escoger con n bits? ¿Si tenemos que escoger entre W opciones, cuántos bits de información necesitaremos para hacerlo?
Podemos demostrar fácilmente que esta fórmula, establecida por Hartley, se obtiene como caso particular en el caso de equiprobabilidad de la fórmula de Shannon anteriormente expuesta.
Actividad 2.6. Hasta mediados del siglo XX, se presuponía que la imposibilidad de predecir el futuro de un Sistema provenía de su carácter no determinista, como ocurría en la Mecánica Cuántica. Pero en la segunda mitad del siglo emerge la dificultad de predecir también el futuro de sistemas deterministas. Pasa a primer plano el viejo proverbio sobre la mariposa cuyo aletear en París podía provocar un huracán en Brasil: cuando la evolución de un Sistema es muy sensible a las condiciones iniciales,
 una
pequeña variación de éstas puede
provocar una gran
diferencia en el resultado final, noción que se desarrolla
en la
Teoría de las
Catástrofes
de René Thom (1972). Si el Paradigma Mecanicista
había
trabajado fundamentalmente con procesos lineales, en los que el efecto
era proporcional a la causa, los Sistemas No Lineales siguen
frecuentemente trayectorias complejas o caóticas.
En determinados
casos, no obstante, su evolución genera estructuras
emergentes a
través de un proceso de autoorganización.
Pero frecuentemente no tienden a estados simples, constantes o
periódicos, sino a lo que se llaman atractores extraños,
como el Atractor
de
Lorenz (1963) generado cuando las derivadas de las
coordenadas
(x,y,z) valen respectivamente x'=10(y-x), y'=x(r-z)-y, z'=xy-8z/3 con
valores de r suficientemente grandes.
una
pequeña variación de éstas puede
provocar una gran
diferencia en el resultado final, noción que se desarrolla
en la
Teoría de las
Catástrofes
de René Thom (1972). Si el Paradigma Mecanicista
había
trabajado fundamentalmente con procesos lineales, en los que el efecto
era proporcional a la causa, los Sistemas No Lineales siguen
frecuentemente trayectorias complejas o caóticas.
En determinados
casos, no obstante, su evolución genera estructuras
emergentes a
través de un proceso de autoorganización.
Pero frecuentemente no tienden a estados simples, constantes o
periódicos, sino a lo que se llaman atractores extraños,
como el Atractor
de
Lorenz (1963) generado cuando las derivadas de las
coordenadas
(x,y,z) valen respectivamente x'=10(y-x), y'=x(r-z)-y, z'=xy-8z/3 con
valores de r suficientemente grandes. 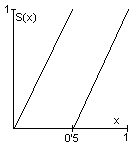 Los atractores
extraños
suelen ser casos particulares de fractales,
objetos de dimensiones fraccionarias
Los atractores
extraños
suelen ser casos particulares de fractales,
objetos de dimensiones fraccionarias que tienen la
propiedad de
autosimilaridad, en los que su forma genérica se repite a
distintas escalas.
que tienen la
propiedad de
autosimilaridad, en los que su forma genérica se repite a
distintas escalas.Podemos generar de forma sencilla un Sistema Caótico aplicando sucesivamente el operador Shift definido por S(x)=2x si 0≤x<0'5, S(x)=2x-1 si 0'5≤x<1, según se muestra en la figura adjunta a la izquierda. Los sucesivos valores de x pueden obtenerse gráficamente haciendo "rebotar" los trazos horizontales en la diagonal, como se indica en la figura adjunta a la derecha. También pueden obtenerse en sistema de numeración binario desplazando los "bits" (0s y 1s) un lugar a la izquierda y descartando la parte entera si aparece. Observar lo que ocurre si experimentamos con el operador Shift a partir de valores iniciales distintos pero muy próximos.
3. Aplicar el paradigma sistémico a los problemas de hoy:
Actividad 3.1. Para formular un problema y resolverlo desde el paradigma sistémico, debemos comenzar detectando los elementos o "síntomas" del mismo, y después establecer sus interrelaciones (sin predeterminar una relación causa-efecto apriorística, como incitaba a hacer el paradigma mecanicista), a partir de las cuáles podremos construir un Modelo y "validarlo" experimentalmente o estudiando los datos previamente disponibles. Las discrepancias que encontremos deberán "retroalimentarnos" modificando el modelo para superarlas. Repetiremos este proceso hasta obtener una aproximación aceptable a los datos de la realidad. Sólo después de disponer de un Modelo correctamente validado podremos determinar sobre qué factores podemos y debemos intervenir para conseguir los objetivos perseguidos. Establecer, utilizando la técnica de "brain storming", un primer Modelo sobre el ciclo urbano del agua en pequeños municipios, detectando los elementos a considerar y avanzando hipótesis sobre sus interrelaciones (no se trata de construir un modelo desarrollado a partir de todo lo previamente estudiado en el curso, sino de realizar un esbozo uniendo todas las ideas que formulen sin cortapisas los asistentes, incluyendo las que hubieran podido ser previamente descartadas). ¿Qué debería hacerse posteriormente con dicho modelo?
Actividad 3.2. Si no se tiene en cuenta el conjunto de las interrelaciones/decisores en un Sistema complejo, una actuación focalizada únicamente sobre un componente del mismo, como reacción a una situación generada a corto plazo y aplicando el paradigma mecanicista (aislando una parte del problema) puede tener efectos contraproducentes a medio o largo plazo. Poner ejemplos sobre casos en los que el "remedio" puede ser peor que la "enfermedad".
Actividad 3.3. Precisamente para evitar que ello ocurra es necesario recurrir al enfoque sistémico, teniendo en cuenta la globalidad de las interrelaciones/decisores, que el éxito de un miembro de un Sistema complejo interrelacionado puede depender del éxito de todos los demás (en "una asociación en que el libre desarrollo de cada uno condicione el libre desarrollo de todos") y que es necesario considerar las consecuencias no sólo a corto plazo sino también a medio y largo plazo. Reflexionar colectivamente sobre cómo podríamos actuar para evitar los efectos "perversos" de la aplicación del paradigma mecanicista en los casos enunciados en la actividad anterior.
Actividad 3.4. Segun Miller (1978), los Sistemas Vivientes de diferentes niveles (células, órganos, organismos, grupos, organizaciones, sociedades y Sistemas Supranacionales) poseen un Suprasistema en su caso y 19 Subsistemas críticos que transfieren Materia, Energía e Información (reproductor, frontera), Materia y Energía (ingestor, distribuidor, conversor, productor, almacén, expulsor, sostén, motor) o Información (transductor de entrada, transductor de salida, transductor interior, canal y red, decodificador, asociador, memoria, decisor, codificador), y sufren un proceso a través del cuál nacen, se mantienen integrados persiguiendo sus objetivos a través de interacciones con su entorno, sufren "patologías" con desajustes entre sus Subsistemas, eventualmente se reproducen y finalmente entran en decadencia y terminan cuando no pueden ajustar sus variables esenciales o no pueden mantener la cohesión entre sus subsistemas. Definir un Sistema Social (un Sistema Viviente de alguno de los 4 niveles superiores) en el cuál se puedan identificar los 19 Subsistemas críticos.
Actividad 3.5. A través de isomorfismos (correspondencias entre los elementos y sus relaciones) entre los Sistemas Vivientes de distintos niveles, estudiados por distintas "disciplinas" científicas, se puede intentar aplicar "inductivamente" Modelos validados en niveles inferiores para cubrir huecos ("gaps") en niveles superiores. Formular isomorfismos entre problemas que aparecen en el nivel de Sistemas Supranacionales (por ejemplo, la crisis financiera global) y problemas de niveles inferiores. Indicar cómo podría utilizarse información sobre la resolución de problemas en tales niveles inferiores (estudiados por una o más disciplinas) para abordar el problema en el nivel superior, y qué equipos interdisciplinarios convendría formar para ello.
Actividad 3.6. A partir de un Modelo genérico validado para Sistemas Vivientes de todos los niveles, puede especificarse y aplicarse "deductivamente" a distintos niveles mediante distintos Modelos que serán isomorfos entre sí. Discutir en qué medida el pensamiento sistémico general puede contribuir al desarrollo de las distintas "disciplinas" científicas especializadas.
4. Vislumbrar el futuro de la Ciencia de Sistemas:
 Actividad 4.1.
De los 40 a los 80 la Ciencia de Sistemas se orientaba a la
construcción de una Teoría General de Sistemas que
utilizando un lenguaje matemático (LM) abordara el estudio de
todos los problemas globales (
Actividad 4.1.
De los 40 a los 80 la Ciencia de Sistemas se orientaba a la
construcción de una Teoría General de Sistemas que
utilizando un lenguaje matemático (LM) abordara el estudio de
todos los problemas globales ( PG) en todos los Sistemas (
PG) en todos los Sistemas ( S),
camino en el que se desarrollan una serie de Teorías presentadas
jerárquicamente en la figura adjunta. Tal Teoría General
de Sistemas incorpora conceptos procedentes de las Ciencias
Biológicas y de las Ciencias Sociales (y también de las
Ciencias de la Computación), y sirve asimismo de "puente" para
trasladar tales conceptos de unas a otras.
S),
camino en el que se desarrollan una serie de Teorías presentadas
jerárquicamente en la figura adjunta. Tal Teoría General
de Sistemas incorpora conceptos procedentes de las Ciencias
Biológicas y de las Ciencias Sociales (y también de las
Ciencias de la Computación), y sirve asimismo de "puente" para
trasladar tales conceptos de unas a otras.Encontrar conceptos procedentes de las Ciencias Biológicas o de las Ciencias Sociales (o de las Ciencias de la Computación) y que se hayan "trasladado" a las otras.
Actividad 4.2. A partir de los 80 comienza un proceso de formación de científicos de diversas "disciplinas" en el pensamiento sistémico, que llegan así a combinar una preparación como "especialistas" y como "generalistas", y aplicar nociones sistémicas en su posterior investigación "disciplinaria", nociones que van impregnando el desarrollo de distintas "disciplinas", tanto las que estudian sistemas biológicos y sociales como las que intentan desentrañar la estructura física de la materia. Por su parte, esas ciencias "particulares" ya con "sabor sistémico" generan aportaciones para nuevas síntesis generalistas que desarrollen la Teoría General de Sistemas.
Buscar conceptos "sistémicos" en la formación "disciplinaria" recibida por los distintos asistentes al curso.
Actividad 4.3. En las últimas décadas del siglo XX se generaliza el uso de ordenadores como instrumento para la investigación científica, y adquieren un nuevo impulso las matemáticas "discretas" orientadas al cálculo con ordenadores y la simulación de Modelos por ordenador. Se desarrolla Internet como una red global de comunicación mundial. La noción de autoorganización, apoyada en la cooperación de distintos sistemas, adquiere nueva relevancia para estudiar la emergencia a partir de situaciones caóticas (como la que ha conducido a la crisis financiera global de 2008).
Estudiar procesos de autoorganización en sistemas de diferente naturaleza, y analizar en qué medida pueden ayudar a resolver los problemas con los que se encuentran dichos sistemas para su supervivencia.
5. Estudiar la formación de sistemas y suprasistemas en Latinoamérica:
Actividad 5.1. Realizar un cuadro o cuadros de los Sistemas-Estados en el territorio de la actual Latinoamérica y sus distintos componentes étnicos a través de su historia.
Actividad 5.2. Estudiar los distintos Suprasistemas supranacionales proyectados, existentes o en formación en Latinoamérica (la Comunidad Andina, el Mercosur, el ALCA, el ALBA...). Intentar identificar en ellos los distintos Subsistemas críticos característicos de los Sistemas Vivientes.
Actividad 5.3. Estudiar las interrelaciones entre Sistemas-Estados en Latinoamérica y sus subsistemas territoriales y los procesos de integración y desintegración en los mismos. Estudiar en particular los casos de Argentina y de Bolivia.
[Conferencia: Actualidad
del Pensamiento Sistémico]
 Este material
es de dominio público y
puede reproducirse libremente, en todo o en parte, sin más
restricción que incluir una referencia a la
autoría
original y preservar el contenido de esta licencia, de modo que no se
introduzcan restricciones adicionales a la difusión de
cualquier
texto que lo utilice.
Este material
es de dominio público y
puede reproducirse libremente, en todo o en parte, sin más
restricción que incluir una referencia a la
autoría
original y preservar el contenido de esta licencia, de modo que no se
introduzcan restricciones adicionales a la difusión de
cualquier
texto que lo utilice.---
Esta Guía Didáctica está diseñada para la realización de un curso en la Universidad de Entre Ríos con una ayuda de la AECI en el marco de la convocatoria realizada por Resolución de 6 de julio de 2007, de la Agencia Española de Cooperación Internacional, publicada en el Boletín Oficial del Estado de 23 de julio