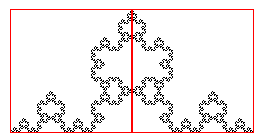
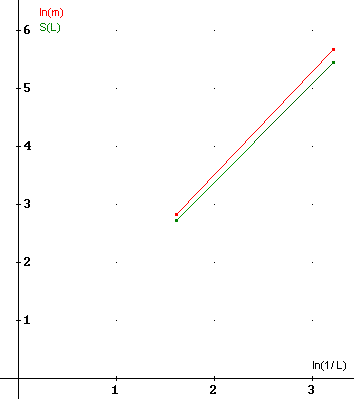
DF = -limn→∞
-ln(3nN(δ0))/ln(δ0/3n) =
-limn→∞ -(lnN(δ0)+nln3)/(lnδ0-nln3) = 1
Comprovar com a exercici que la dimensió fractal de l'àrea interior d'un rectangle és 2 (podem començar suposant que recobrim exactament el rectangle amb una retícula de a×b quadrats amb costat de longitud δ0).
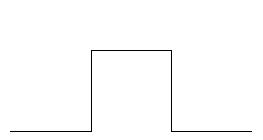
Anem a estudiar ara el següent fractal "crucífer", del que mostrem els primers pasos de la seua construcció:
Es pot visualitzar en http://www.uv.es/pla/Tutoria/scca/crucifer.gif el procés de la seua construcció. Observem que en cada pas la longitud es multiplica per 5/3, i per tant la longitud total del fractal serà infinita. Així mateix, i per tal com el procés de construcció es repeteix a totes les escales, la longitud de la porció del fractal entres dos punts qualsevol del mateix serà també infinita.
Observem igualment que si partim de un segment de longitud 1, en el primer pas l'altura de la figura és 1/3, en el segon pas s'afegeix una altura de (1/3)·(1/3), en el tercer altra altura de (1/3)·(1/3)·(1/3), i així successivament. Per tant, l'altura total del fractal serà la suma de la sèrie geomètrica amb termini inicial 1/3 i raó 1/3, S=(1/3)/(1-(1/3))=(1/3)/(2/3)=1/2. Per tant, recobrirem totalment el fractal amb 2 quadrats adosats de longitud δ0=1/2. En la figura següent es mostren els recobriments amb δ=δ0 i amb δ=δ0/3.
Comprovar com a exercici que la dimensió fractal de l'àrea interior d'un rectangle és 2 (podem començar suposant que recobrim exactament el rectangle amb una retícula de a×b quadrats amb costat de longitud δ0).
Anem a estudiar ara el següent fractal "crucífer", del que mostrem els primers pasos de la seua construcció:
 |
 |
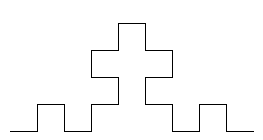 |
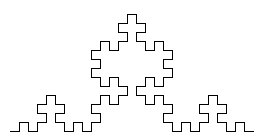 |
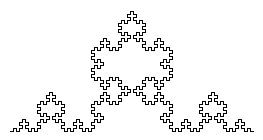 |
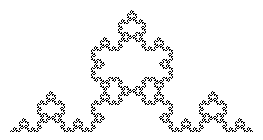 |
Es pot visualitzar en http://www.uv.es/pla/Tutoria/scca/crucifer.gif el procés de la seua construcció. Observem que en cada pas la longitud es multiplica per 5/3, i per tant la longitud total del fractal serà infinita. Així mateix, i per tal com el procés de construcció es repeteix a totes les escales, la longitud de la porció del fractal entres dos punts qualsevol del mateix serà també infinita.
Observem igualment que si partim de un segment de longitud 1, en el primer pas l'altura de la figura és 1/3, en el segon pas s'afegeix una altura de (1/3)·(1/3), en el tercer altra altura de (1/3)·(1/3)·(1/3), i així successivament. Per tant, l'altura total del fractal serà la suma de la sèrie geomètrica amb termini inicial 1/3 i raó 1/3, S=(1/3)/(1-(1/3))=(1/3)/(2/3)=1/2. Per tant, recobrirem totalment el fractal amb 2 quadrats adosats de longitud δ0=1/2. En la figura següent es mostren els recobriments amb δ=δ0 i amb δ=δ0/3.