5. Models globals: models matemàtics d'evolució social:

Els sistemes socials són un cas paradigmàtic de sistemes complexos, per la gran quantitat de factors involucrats en el seu comportament i per les incerteses en la seua evolució. I aquesta complexitat és especialment notòria quan del que es tracta no és simplement de l'evolució d'algun aspecte particular o d'alguna societat local, sinó de l'evolució global del conjunt de la humanitat tenint en compte diversos aspectes de la mateixa. Els models que pretenen simular aquesta evolució reben el nom de models globals. Podeu trobar una revisió d'aquestos en la Introducció de la tesi doctoral de Vicent Castellar Busó sobre "Un model sistèmic d'evolució social sostenible", en http://www.uv.es/~buso/tesi/intro.zip

Assenyalem que és essencial als sistemes socials el tractament de sistemes complexos de diferents nivells. En el cas més senzill, tindriem un sistema "col·lectiu" composat de diferents sistemes "individuals", cadascú dels quals evoluciona interactuant amb el seu entorn, composat per altres sistemes individuals i per l'entorn extrasocial. L'evolució de cada sistema individual, encara que difícil de predir de forma determinista, estaria sotmesa a les regles d'un aprenentatge psicològic, de forma que, en particular, un comportament tendiria a repetir-se (tindria un reforçament positiu) quan conduira a la satisfacció dels objectius individuals, mentres que tendiria a evitar-se (tindria un reforçament negatiu) quan conduira a la insatisfacció dels objectius individuals.

Ara bé, la qüestió que cal esbrinar és si la interacció "social" d'un conjunt de sistemes individuals, cadascú dels quals perseguint els seus propis objectius individuals, provoca una evolución global purament caòtica o pot ser descrita per unes regles globals, com les que es podrien expressar en un aprenentatge social, en funció de determinats objectius socials.

Es podrien descriure diferents dinàmiques d'organització social amb diferents formes de relació entre aprenentatge psicològic i aprenentatge social.

Així, un sistema autoritari-dogmàtic es caracteritzaria per unes normes socials de comportament estàtiques que condicionarien la satisfacció o insatisfacció dels sistemes individuals que el composen. D'aquesta manera, la repressió social dels comportaments individuals contraris a aqueixes normes socials minvarien la seua satisfacció, generant-lis un reforçament negatiu que conduiria a la seua evitació.

En aquest model, les normes socials de comportament romandrien fixes, i per tant no es produiria inicialmente aprenentatge ni evolució social. Tanmateix, en determinades circumstàncies es podria generar insatisfacció fins i tot amb l'acatament de d'unes normes socials que poden haver esdevingut obsoletes, cosa que generaria una situació de crisi social. En aquestes condicions, es pot produir o bé una fractura del sistema social o bé una confrontació desventajosa amb altres sistemes socials amb normes més adients. El resultat pot ser la destrucció o dissolució del sistema social obsolet, amb la seua eventual substitució per altre sistema social amb altres normes amb capacitat de generar satisfacció pel seu acompliment.

Observem que en aquest cas l'evolució social es produiria a través de la interacció entre diferents sistemes socials, que generaria una selecció d'aquells més capaços de produir satisfacció individual. Aquesta evolució, per tant, es produiria en un segon nivell d'organització social, en una "població" de sistemes socials.

A diferència de l'anterior, un sistema democràtic-científic es caracteritzaria per unes normes socials de comportament variables, que resultarien reforçades positiva o negativament segons la seua capacitat o no de generar satisfacció individual pel seu acompliment. Aquest reforçament es podria produir a través d'un procés electoral en el qual els individus votaren per unes o altres opcions en funció de la seua expectativa de satisfacció.

En la pràctica, un sistema social pot funcionar com una combinació dels anteriorment descrits.

Per altra banda, un sistema social complexo pot estar estructurat a diferents nivells, de manera que les normes de cada nivell puguen condicionar o estar condicionades per la satisfacción en el nivell inferior. En alguns casos, a diferents nivells poden funcionar sistemes antitètics com els tres anteriorments descrits. En altres casos, el mateix sistema es pot reproduir a diferents nivells, amb una autosimilaritat com la que caracteritza als sistemes fractals.

Com a exercici, es poden discutir les característiques de les següents formes d'organització social:
a) El feudalisme.
b) La democràcia parlamentària.
c) El capitalisme neoliberal.
d) L'imperialisme modern.
e) L'ONU.
f) La Unió Europea.
g) El federalisme.

Anem a examinar en detall el model d'evolució social que hem vingut desenvolupant en el Departament de Matemàtica Aplicada de la Universitat de València, i que s'ha expressat en l'esmentada tesi doctoral de Vicent Castellar Busó (http://www.uv.es/~buso/tesi/tesiweb.html) i en la tesi doctoral de Mohamed Nemiche sobre "Un modelo sistémico de evolución social dual" (http://www.uv.es/~nemiche/thesis%5B1%5D.html; es pot veure una descripció de les equacions del model en http://www.uv.es/~pla/models/panticosa/mdeh.htm, i una presentació del mateix en "diapositives" en http://www.uv.es/~nemiche/tesis.ppt).

En aquest model s'utilitzen processos deterministes i probabilístics per a descriure l'evolució social. Anem a analitzar-los amb deteniment.

1) Tenim un model d'adaptació determinista lineal d'una variable X tendint a un objectiu Y en el qual
X(t+1) = X(t) + (Y(t)-X(t))/R ,    [1]
on R indica el retard de l'adaptació, cosa que expressarem com
X
→
R
 Y
(observeu que si R=1 aleshores X(t+1)=Y(t), i per tant el retard es redueix a un únic pas).

És clar que si Y és constant, X(t+n)-Y = (X(t)-Y) ((R-1)/R)n , i per tant si R>0'5 aleshores el valor de X convergirà a Y (justificar-ho com a exercici).

Si l'objectiu Y és variable, les condicions de convergència dependran de la seua variabilitat. Especial interés té el cas en que Y tendisca a un objectiu que a la seua vegada siga funció de X. En aquests casos cal distingir entre l'existència d'un eventual estat d'equilibri (en el qual cada variable coincideix amb el seu objectiu) i la possibilitat d'assolir aquest estat.

Estudiarem el cas senzill en el qual
Y
→
R
 X

En aquest cas (i sempre que Y tendisca a una funció lineal de X) el problema es redueix al d'una iteració lineal de punt fixe, resultant clar que serà d'equilibri qualsevol estat en el qual X=Y. Demostrar, com a exercici, que la condició de convergència és R>1.

En les figures adjuntes podem observar l'evolució de X i Y per a diferents valors de R:



Podem reflexionar a partir d'elles sobre la conveniència d'una adaptació ràpida o d'una adaptació gradual per a aconseguir un objectiu quan el procés d'adaptació és recíproc.

Podeu examinar en http://www.uv.es/~pla/models/Modevinc.htm un model més complexo d'evolució de l'intercanvi entre diferents països, amb el qual s'arriba a una conclusió similar.


2) Tenim un model d'aprenentatge probabilístic amb reforçament lineal d'una variable U per la satisfacció o no d'un objectiu G si la probabilitat d'U ve donada per
P(U) = F(U)/B    [2]
on
B = ∑U F(U)     [3]
expressa la memòria acumulada, i F és una variable acumuladora de memòria que varia d'acord amb
Ft+1(U) = Ft(U) + Ct·(PGt(U)-Rt)·PLt(U),     [4]
on PG indica la probabilitat o grau de satisfacció de l'objectiu, R el nivell de referència de la satisfacció, PL la possibilitat d'aprenentatge i C un factor que regula el ritme de l'aprenentatge.

En un cas senzill, seria R=0'5, C=2 i PL=P (amb el qual la possibilitat d'aprenentatge per a cada valor d'U coincidiria amb la seua probabilitat). de manera que
Ft+1(U) = Ft(U) + 2(PGt(U)-0'5)·Pt(U) = .Ft(U) (1+2(PGt(U)-0'5)/Bt)     [5]
En aquest cas, en el cas de plena satisfacció PG(U)=1 s'acomplirà Ft+1(U)=Ft(U)(1+1/Bt), i en el cas de completa insatisfacció PG(U)=0 s'acomplirà Ft+1(U)=Ft(U)(1-1/Bt) .

Estudiar com a exercici l'evolució de la probabilitat en el cas de dos valors d'U tals que PG(1)=1 i PG(0)=0 amb equiprobabilitat inicial i un valor inicial de la memòria acumulada de B=10. Aquesta evolució es mostra en la figura adjunta.

Com variará la memòria acumulada B?

Com variaria si per a tots els valor d'U la probabilitat de satisfacció PG(U) fora inferior al nivell de referència 0'5?
  


3) Simulació de la repressió social:

Els dos models descrits poden simular processos d'adaptació i d'aprenentatge, respectivament, per a sistemes de diferents tipus. En el cas de sistemes socials, hem d'introduir la interacció entre diferents sistemes individuals.

Així, en el model d'aprenentatge probabilístic, haurem de considerar diferents sistemes individuals N i les seues probababilitats P(U|N), funcions d'acumulació de memòria F(U|N), memòria acumulada B(N), i probabilitat de satisfacció PG(U|N).

La evolució pot portar a que ens determinats casos B(N)=0 (a tal efecte, aproximem F(U|N) per la seua part entera, i prenem 0 si surt negativa). En aquest cas, considerem que el sistema individual N ha estat destruït. En altre cas, és a dir amb B(N)≠0, direm que el sistema N està actiu.

L'evolució individual i social vindrà regulada per la funció de probabilitat de satisfacció, que expressarem a través del producte
PG(U|N) = π(U)(1-σ(U,N)) ,     [6]
on π(U) expressa la possibilitat pròpia de satisfacció amb el comportament U, i σ(U,N) expressa la repressió social patida pel comportament U en el sistema N per part dels demés. Aquesta repressió vindrà donada per
σ(U,N) = ∑N'/ B(N')≠0 ∑U'≠U Ф(U',N') sts(U',N') IMP(N',N)     [7]
on Ф(U',N') expressa l'abast del comportament U' en el sistema N', sts(U',N') expressa la capacitat repressiva del comportament U' en el sistema N', i IMP(N',N) indica un factor d'impacte de N' sobre N.

Expressarem l'abast del comportament U en el sistema N per
Ф(U,N) = P(U|N)2/S ,     [8]
on S serà el número de sistemes actius, S=n({N / B(N)≠0}) .

Suposant que per a un determinat comportament U' i per a tots els sistemes actius P(U'|N')=1, que la capacitat repressiva de U' siga independent de N' i que el factor d'impacte siga la unitat, calcular com a exercici la repressió sobre un comportament U≠U' .


4) Simulació del relleu generacional:

Si hi ha comportaments favorables (amb PG(U|N)>R) i comportaments desfavorables (amb PG(U|N)<R) la probabilitat P(U|N) dels primers tendirà a augmentar, i per tant la seua acumulació de memòria F(U|N) augmentarà en major mesura que disminuirà la dels altres. El resultat serà per tant que la memòria acumulada B(N) tendirà a augmentar. Però amb això les posteriors variacions de F(U|N) afectaran menys a la probabilitat P(U|N), i per tant l'aprenentatge es ralentitzarà.

Comparar, com a exercici, el valor següent de les probabilitats a partir d'aquestes dues situacions:
a) P(1|N)=P(0|N)=0'5, B(N)=10
b) P(1|N)=0'8, P(0|N)=0'2, B(N)=100
suposant que en els dos casos PG(1|N)=1, PG(0|N)=0, R=0'5, C=2 i PL=P.
Es pot observar en la figura anterior que l'increment de les probabilitats per increment unitari del temps s'aproxima a cero.

D'aquesta manera, l'increment de la memòria acumulada B(N) pot expressar un envelliment que genera una major "inercia" en l'aprenentatge. Per a simular una renovació o rejuveniment de la població a través d'un relleu generacional, podem estabilir que quan
γ = α + B(N)/ktanatos ≥ 1     [9]
la variable acumuladora de memòria s'inicialitza a
F(U|N) = knatal(N)     [10]
per a tot comportament U. α és una variable aleatòria que adopta valors distribuïts uniformement en l'interval [0,1[ .

Calcular, com a exercici, la probabilitat de relleu generacional en els casos B(N)=0, B(N)=ktanatos  i B(N)=ktanatos/2 .

S'observarà que, amb la fòrmula anterior [9], en els sistemes destruïts no es produeix relleu generacional, i per tant la destrucció és permanent. Per tal de simular una possible recuperació, substituirem aqueixa fòrmula [9] per
γ = α + A(N) + [1-A(N)]·B(N)/ktanatos ≥ 1 ,    [11]
la qual es redueix a l'anterior [9] si A(N)=0 .

Estudiar com a exercici quina serà la probabilitat de recuperació per relleu generacional si B(N)=0 .


5) Simulació de la comunicació científica:

Segons la fòrmula [5], amb PL=P, un sistema individual N solament podria aprendre de la seua pròpia experiència. Per tal de simular una "comunicació científica" que permeta a un sistema individual aprendre de l'experiència dels demés, prendrem
PL(U|N) = P(U|N) + RE(N) ∑N'≠N P(U|N')·EM(N')·IMP(N',N)     [12]
on EM i RE són els factors d'emissió i recepció, respectivament, corresponents a cada sistema individual. Si aquests factors valen zero es torna al cas anterior PL=P . Prendrem
RE(N) = ∑U P(U|N)·re(U) ,  EM(N) = ∑U P(U|N)·em(U) ,     [13]
on re i em són els factors de recepció i emissió, respectivament, corresponents a cada comportament. Direm que un comportament U és plenament "científic" si i solament si re(U)=em(U)=1, el que suposarà que el seu aprenentatge està compleament obert a l'experiència d'altres sistemes individuals.

Obtenir com a exercici l'expressió de PL si en tots els sistemes individuals únicament hi ha comportaments plenament científics i el factor d'impacte és la unitat.


6) Simulació del progrés tecnològic:

Podem simular el progrés tecnològic a través d'un increment del número de comportaments entre els que es pot elegir. A tal efecte, suposarem que el comportament té diferents components, U=(Ui)i=0:mmax-1 , on mmax indica la dimensió màxima. Suposant que cada component Ui pot adoptar els valors 0 i 1, asignarem a cada comportament el valor numèric U=∑i=0:mmax-1Ui2i del qual els components Ui formen la seua expressió en base 2.

Suposarem també que cada sistema individual té una dimensió pròpia m(N)≤mmax  tal que en cas d'inicialització o relleu generacional
F(U|N) = knatal(N) si U≤M(N)  &  F(U|N) = 0 si U>M(N),     [14]
on
M(N) = 2m(N)-1
és el valor màxim de U de dimensió m(N) ( amb Ui=0 si i≥m(N) ).

Justificar com a exercici quant valdrà P(U|N) en absència de "comunicació científica" per a U>M(N) .

Doncs bé, establirem que la dimensió pròpia m(N) d'un sistema individual s'incrementarà en una unitat (sempre que no supere mmax) si i solament si
δ = β + b(N) + B(N)/kprg ≥ 1     [15]
on β és una variable aleatòria que adopta valors distribuïts uniformement en l'interval [0,1[ i
b(N) = ∑U>M(N) P(U|N)     [16]
la qual pot considerar-se com una expressió de la "difusió tecnològica" per la qual un sistema individual pot adoptar comportaments que excedeixen a seua capacitat tecnològica pròpia (expressada en la seua dimensió pròpia).

Discutir com a exercici qué passarà quan B(N)=kprg i la influència de la comunicació científica en la difusió i en el progrés tecnològic.


7) Simulació d'un pacifisme adaptatiu:

Podem suposar que la capacitat repressiva d'un comportament en un sistema individual no és constant, sinó que tendeix a igualar-se a la repressió patida pel mateix. Això ho simularem assignant un valor inicial a aquesta capacitat repressiva en cas d'inicialització i relleu generacional, i suposant que a partir del mateix té una adaptació determinista lineal
sts(U,N)
→
Ta
 σ(U,N)
on Ta indica el retard en l'adaptació de la repressió.

Es pot introduir una variació del model per a simular una solidaritat davant la repressió dins d'una determinada "zona de solidaritat", de tal manera que
sts(U,N)
→
Ta
 màxim de σ(U,N') per a N' dins de la zona de solidaritat de N

Assenyalem que tant el factor d'impacte IMP(N',N) com l'abast de la zona de solidaritat poden expressar l'abast del transport i les comunicacions. Una situació de globalització es caracteritzaria per que tant l'impacte com la zona de solidaritat abastarien a tota la població de sistemes individuals.

Assenyalem així mateix que una elevada capacitat repressiva d'un comportament pot bloquejar l'evolució cap a altres comportaments amb major possibilitat tècnica de satisfacció. Reflexionar com a exercici sobre en quina mesura el retard en l'adaptació de la repressió pot influir en la possibilitat de superació d'aquest bloqueig.


8) Simulació del factor subjectiu:

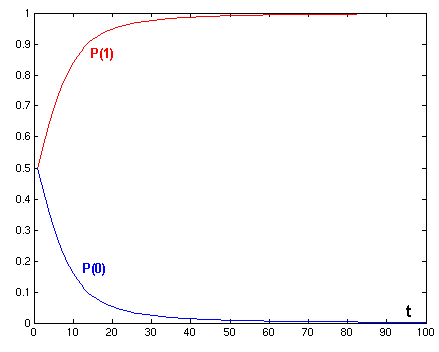
En la fòrmula [5] es suposa que R=0'5, i que per tant el nivell de referència de la satisfacció és constant i igual per a tots els sistemes individuals. Tanmateix, pot considerar-se que la percepció subjectiva de la satisfacció depen de la prèvia experiència patida o coneguda per cada sistema individual. Si aquesta percepció s'actualitzara immediatament, caldria prendre com a nivell de referència la satisfacció mitjana ponderada per la possibilitat mitjana d'aprenentatge,
mG(N) = ∑U PG(U|N)·PL(U|N) / ∑U PL(U|N)     [17]
dividint així mateix el factor C per la corresponent desviació típica
σG(N) = (∑U PG(U|N)2·PL(U|N) / ∑U PL(U|N) - mG(N)2)1/2      [18]
per a no distorsional el ritme d'aprenentatge per l'eventual proximitat dels valors de la probabilitat de satisfacció PG(U|N) a la satisfacció mitjana mG(N) .

Ara bé, podem suposar que la percepció subjectiva de la satisfacció té una certa inercia i es produeix amb un cert retard, amb una adaptació determinista lineal del nivell de referència de la satisfacció
R(N)
→
Tr
 mG(N)
on Tr indica un "temps de resignació" a la satisfacció mitjana.

Igualment, el factor C s'haurà de dividir per un quocient SR(N) sotmés a una adaptació determinista lineal a la corresponent desviació típica,
SR(N)
→
Tr
 σG(N)
amb el mateix retard.


9) Simulació de la degradació ecològica:

Podem suposar que es disposa inicialment d'una totalitat de recursos E0, del qual es detrau en cada periode una quantitat pel consum en satisfacció,
K1 = ∑U,N π(U)·P(U1N)      [19]
i pel consum en repressió,
K2 = ∑U,N sts(U)·P(U1N)       [20]
(naturalment, les sumes s'estendran únicament sobre els sistemes actius N tals que B(N)≠0 ).

Ara bé, en tant aquestes quantitats no superen una certa cota, podem suposar que els recursos consumits es poden recuperar per reutilització (r), en la qual incloguem la renovació dels recursos naturals. Més enllà d'aquesta cota es produiria una degradació ecològica, de manera que la totalitat de recursos passaria a ser E<E0 , i caldria un reciclatge (ρ) per a la seua recuperació. A diferència de la reutilització, que es pot considerar sense cost, el reciclatge tindria un cost
K3 = ∑U,N ρ(U,N)·P(U1N)      [21]
que es detrauria del consum en satisfacció, de manera que aquest passaria a ser
K1 = ∑U,N (π(U)-ρ(U,N))·P(U1N)      [22]
i la probabilitat de satisfacció seria
PG(U|N) = (π(U)-ρ(U,N))·(1-σ(U,N))·E/E0     [23]

Si expressem la cota de la possible reutilització per un factor del recursos, cE, podem establir que la reutilització r siga el mínim entre aquesta cota i el valor necessari per a compensar la degradació ecològica, E0-E+K1+K2 .

I en cada pas, el valor total dels recursos seria
E(t+1) = E(t) + r(t) +K3(t) - K1(t) -K2(t)      [24]

Naturalment, el reciclatge ideal ρI serà aquell que permeta obtenir E(t+1)=E0 . Obtenir com a exercici la seua expressió.

El reciclatge efectiu ρ(U,N) es produiria amb un cert retard, Te(N), que pot expressar el nivell de consciència ecològica,  i seria ρI/Te(N)  sempre que aquesta quantitat no supere la possibilitat pròpia de satisfacció π(U). Si el retard Te(N) és gran, com a expressió d'una baixa consciència ecològica, els recursos totals E poden anar disminuint fins arribar a zero, el qual es podria descriure com una hecatombe ecològica.


10) Efecte Revolta:

Normalment, en cada fase de la simulació (per a cada dimensió) tendirá a predominar aquell comportament que tinga una major probabilitat de satisfacció PG(U|N). Tanmateix, en determinades circumstàncies predominen localment comportaments amb probabilitat de satisfacció baixa que podian presumir-se minoritaris. Això passa en situacions de "crisi" por degradació ecològica, en las quals per a tots els comportament la probabilitat de satisfacció és inferior al nivell de referència, i sol ser efímer.

Per a entendre perquè passa això, estudiar com a exercici l'evolució a partir de la següent situació: C=2, R=0'5, PL=P, B(N)=12, P(1|N)=0'75, P(0|N)=0'25, PG(1|N)=0'4, PG(0|N)=0'2.

Interpretar-ho i possar possibles exemples històrics d'aquest Efecte.

Reflexionar com a exercici sobre en quina mesura el "temps de resignació" pot influir en l'aparició de situacions de "crisi"  conduents a la destrucció dels sistemes individuals.


En les referències abans indicades s'estudia l'aplicació de models específics en les quals l'evolució pot conduir al predomini final del que anomenem "societat científica lliure" (comportament plenament científic sense capacitat repressiva) o d'una "societat plenamente repressiva" (on una capacitat repressiva igual a la unitat pot anul·lar les ventajes en possibilitat pròpia de satisfacció d'altres comportaments) o bé a una hecatombe ecològica. Es simula també una evolució dual Orient-Occident entre comportaments "gregaris" en els quals l'impacte de la capacitat repressiva és màxim sobre el propi sistema individual i comportaments "individualistes" en els quals la capacitat repressiva no té impacte sobre el propi sistema individual, però sí sobre els demés sistemes.

Avaluar en quina mesura aquestes simulacions es poden correspondre amb l'evolució real de la humanitat.