6. Desenvolupament de models matemàtics de sistemes complexes i dinàmiques caòtiques:

Direm que una aplicació f : X→Y (on X, Y són subconjunts de R) genera caos si acompleix:
1) Sensibilitat a les condicions inicials: per a tot δ,ε>0, xcX, existeix y,k / ycX & kcN & |y-x|<ε & |f^k(x)-f^k(y)|>δ
2) Densitat dels punts periòdics: per a tot ε>0, xcX, existeix y,k / ycX & kcN & |y-x|<ε & f^k(y)=y

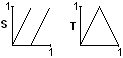
Definim les aplicacions: Shift: S : [0,1)→[0,1)  / S(x)=2x si 0≤ x<½ , S(x)=2x-1 si ½≤ x<1 Tenda de campanya: T : [0,1]→[0,1]  / T(x)=2x si 0≤ x<½ , T(x)=2-2x si ½≤ x≤ 1

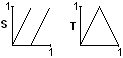Observe-s que, si expressem els números en sistema de numeració binària, l'efecte de l'aplicació S és desplaçar les xifres cap a l'esquerra plenant amb zeros a la dreta i suprimint en el seu cas les unitats, en tant que l'efecte de l'aplicació T és desplaçar les xifres cap a l'esquerra plenant amb zeros a la dreta i, en cas que aparega una unitat, suprimir-la i substituir 0 per 1 i 1 per 0 en les xifres a la dreta de la coma.

Es pot demostrar que T^k+1(x)=T(S^k(x)) si x<1 .

Exercici: comprovar els axiomas de caoticitat per a les funcions S i T amb δ=0'01, ε=0'0001, x=0'e, on "e" es la successió binària corresponent del tema 1.