Llicenciatura en Ciències Ambientals
GUÍA DIDÀCTICA
Rafael Pla López
Departament de Matemàtica Aplicada
Universitat de València
curs 2009-2010
Objetivos:
Específicos:
1. Comprender los conceptos fundamentales de la Teoría General de Sistemas.
2. Aprender a utilizar algunas herramientas básicas de la metodología sistémica.
3. Adquirir o actualizar nociones básicas de Estadística.
4. Aprender a realizar simulaciones construyendo modelos cibernéticos.
5. Adquirir técnicas para encontrar la solución óptima a un problema.
6. Estudiar el comportamiento de sistemas caóticos.
Genéricos:
Metodología:
Bibliografía:
Genérica:
Actividad 1: Agrupar de 2 en 2 los siguientes Sistemas, estableciendo correspondencias entre sus componentes de manera que sus relaciones coincidan:
Actividad 3: llamamos relaciones estructurales a las que se dan entre los elementos de un Sistema considerados como objetos singulares, indicando su conexión o dependencia; llamamos relaciones de comportamiento a las que se dan entre los conjuntos de valores de los distintos elementos de un Sistema considerados como variables, indicando la compatibilidad entre dichos valores.
Analizar qué relaciones son estructurales y cuáles son de comportamiento en las actividades anteriores.
Actividad 4: estudiar cómo dar una definición formal de Sistema de modo que puedan tomarse en consideración relaciones tanto estructurales como de comportamiento. Pueden tenerse en cuenta a tal efecto las definiciones siguientes, en las que ≤ indica una relación de inclusión, X indica un producto cartesiano, U indica una unión de conjuntos, P indica el conjunto de los subconjuntos de un conjunto y Ø es el conjunto vacío.
S≤ XicI Vi (Mesarovic&Takahara 1975)
S=(E,R) tal que ØcR≤P(UncN (E n)) (Yang 1989)
S=(E,R) tal que ØcR≤Tm tal que Tm+1=P( UncN (Tm) n ), T0=E (Caselles 1993)
S=(I, {Vi}icI, R) tal que R ≤ P(Un=1...m I n) U P(XicI Vi) (Pla 2007)
Actividad 5. Llamaremos Sistema de conexiones a un Sistema con una relación estructural binaria, R ≤ EXE, de modo que (a,b)cR si y sólo si a depende directamente de b, b→a. Diremos de un Sistema de conexiones que es jerárquico si en él no pueden encontrarse bucles, de manera que un elemento no pueda depender directa ni indirectamente de sí mismo. En tal caso, si el número de elementos es finito, habrá necesariamente un subconjunto de elementos que no dependan de ningún otro, a los cuáles llamaremos elementos de nivel 1 o de entrada. Asimismo, diremos que un elemento es de nivel n>1 si y sólo si depende de algún elemento de nivel n-1 y en todo caso de elementos de nivel inferior. Llamaremos elementos de salida a aquéllos de los que no depende ningún otro.
Para establecer una clasificación en niveles comenzaremos extrayendo sus elementos de entrada (nivel 1). A continuación prescindiremos de ellos y buscaremos cuáles serían de entrada entre los restantes (nivel 2), y así sucesivamente. El Sistema será jerárquico si y sólo si a través de este proceso podemos llegar a clasificar en niveles todos sus elementos. El Sistema será conexo si no tiene elementos aislados, es decir si todos sus elementos tienen una relación de dependencia con algún otro.
Ejercicio 1: estudiar si es jerárquico el siguiente Sistema de conexiones, clasificando en niveles sus elementos:
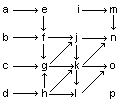
Actividad 6. Llamaremos Sistema Normal a un Sistema S={E,c,f}, tal que E es un conjunto de variables, c≤ EXE es una relación estructural de conexión jerárquica y f ≤ XicE Vi es una relación de comportamiento.
Poner ejemplos de Sistemas Normales, especificando E, {Vi}icE, c y f .
Analizar en qué casos la relación estructural c podría inferirse de la relación de comportamiento f :
Ejercicio 2: dada la relación de comportamiento definida por u=x2+y2 , v=y2-z2, w=u2+v2, siendo x, y, u, v, w números reales, inferir de ella una relación estructural para definir un Sistema Normal.
Actividad 7. Llamaremos Sistema Temporal a un sistema con alguna relación de comportamiento que involucra alguna variable temporal X cuyo conjunto de valores es VX ≤ DXT = {x / x:T→DX}, es decir, un conjunto de aplicaciones de T en un dominio DX, siendo T un intervalo temporal.
Analizar cuáles de los Sistemas anteriormente considerados son Temporales.
Actividad 8. Llamaremos Sistemas Dinámicos a aquellos Sistemas Temporales cuyas relaciones de comportamiento pueden describirse clasificando sus variables en variables de entrada X, variables de salida Y y variables de estado U, de modo que:
a) La evolución en el tiempo de las variables de salida Y a partir de un instante tcT depende del valor de las variables de estado U en el instante t y de la evolución en el tiempo de las variables de entrada X a partir de dicho instante t.
b) El valor de las variables de estado U en un instante tcT depende del valor de las mismas en cualquier instante t'≤t y de la evolución en el tiempo de las variables de entrada X entre los instantes t' y t, de modo que se cumplan las propiedades de
b1) Identidad: si t'=t, el valor de las variables de estado U en los instantes t' y t debe coincidir.
b2) Transitividad: si t"≤t'≤t, para una determinada evolución en el tiempo de las variables de entrada X entre los instantes t" y t, la dependencia del valor de las variables de estado U en el instante t a partir de su valor en el instante t" debe ser equivalente a la que se derivaría del valor de dichas variables en el instante t' dependientes de su valor en el instante t.

b3)
Consistencia: para una determinada
evolución en el tiempo de las variables de entrada X a partir de
un instante t', la
dependencia respecto al valor de las variables de estado U en dicho
instante t' de la evolución en el tiempo de las variables de
salida Y a partir de un instante t≥t' debe ser equivalente a su
dependencia respecto al valor de los variables de estado U en dicho
instante t derivadas de su valor en el instante t'.

Si todas las relaciones de dependencia
en cuestión son
deterministas, diremos que el Sistema Dinámico es Determinista. Si algunas o todas
las relaciones son probabilísticas, y el resto deterministas,
diremos que el Sistema es Estocástico.
Si alguna relación no podemos definirla de modo determinista ni
probabilística, tenemos la opción de intentar estimar la
"posibilidad", entre 0 y 1, de los correspondientes valores de las
variables de salida Y o de estado U; en tal caso, diremos que
trabajamos con un Sistema Borroso.
Poner ejemplos de Sistemas Dinámicos Deterministas, Estocásticos y Borrosos e intentar definir sus relaciones.
Actividad 9. Un Sistema Dinámico no anticipatorio será aquél en que los valores de las variables de salida Y no dependan de valores posteriores de las variables de entrada X. Una forma sencilla de Sistemas Dinámicos Deterministas no anticipatorios con intervalo temporal discreto son los Sistemas Secuenciales, cuyas relaciones de comportamiento vienen dadas por
y(t) = F(x(t),u(t))
u(t+1)=G(x(t),u(t))
donde x, u, y pueden representar tuplas de variables de entrada, estado y salida, respectivamente. Es decir, y(t)=(y1(t),y2(t),y3(t)...), etc.
Ejercicio 3: dado un Sistema Secuencial definido por y(t)=u(t)·x(t), u(t+1)=u(t)+x(t), expresar y(5) como función del estado inicial u(0) y de la secuencia de valores de entrada (x(0),x(1),x(2),x(3),x(4),x(5)).
Tomando como elementos los valores de x(t), u(t), y(t) para t=0,1,2,3,4,5, analizar si su Sistema de conexiones es jerárquico, clasificando en niveles dichos elementos.
Llamaremos retroacción a la situación que se da cuando el valor de una variable depende directa o indirectamente de valores anteriores de la misma ¿En un Sistema Secuencial se produce retroacción? ¿Hay bucles en su sistema de conexiones?
Actividad 10. Diremos que un Sistema Normal S'=(E',c',f ') es un subsistema del Sistema Normal S=(E,c,f) si y sólo si:
a) E' ≤ E
b) c' ≤ c
c) f ' = f | E', es decir, f ' es la restricción de f a E' , es decir que para todo xcXicE ' Vi , xcf ' si y sólo si existe ycXicE-E ' Vi tal que (x,y)cf .
d) Si un elemento de E' no es de entrada en S', c' incluye todas las dependencias directas sobre el mismo. Es decir, que para todo i,j,kcE, si (i,j)cc' y (i,k)cc, entonces (i,k)cc' (lo que supone que kcE').
Ejercicio 4: extraer subsistemas del Sistema de conexiones del Ejercicio 1.
Ejercicio 5: extraer subsistemas del Sistema Normal obtenido en el Ejercicio 2, indicando cuáles serían sus relaciones de comportamiento.
Actividad 11. Dados dos subsistemas A, B de un Sistema Normal, diremos que B depende directamente de A, A→B, si y sólo si existe alguna variable de entrada de B que sea variable dependiente (no de entrada) de A.
Dado un conjunto C de subsistemas de un Sistema Normal, llamaremos SuperSistema del mismo al Sistema de conexiones SS=(C,R), tal que R≤CXC es una relación estructural binaria formada por todos los pares (B,A) tales que A→B . Diremos que dicho SuperSistema está bien determinado si y sólo si es jerárquico.
Ejercicio 6: dados los conjuntos de subsistemas obtenidos en los Ejercicios 4 y 5, obtener sus correspondientes SuperSistemas y estudiar si están o no bien determinados.
Actividad 12. Diremos que un conjunto de subsistemas Si de un Sistema Normal S es una descomposición del mismo si y sólo si:
a) El SuperSistema correspondiente está bien determinado.
b) Ninguna variable es dependiente en más de un subsistema.
c) Toda variable del Sistema Normal S es una variable de alguno de sus subsistemas, es decir Ui Ei = E .
Ejercicio 7: estudiar si los conjuntos de subsistemas obtenidos en los Ejercicios 4 y 5 son una descomposición de un Sistema Normal; estudiar cómo podríamos obtener una descomposición de un Sistema Secuencial.
Actividad 13. Llamaremos descomposición máxima de un Sistema Normal a la formada por los subsistemas resultantes de tomar cada variable dependiente o de salida y las variables de las cuáles depende directamente junto con dichas dependencias directas. Llamaremos descomposición natural de un Sistema Normal con un conjunto finito de variables al resultante de aplicarle el Algoritmo 1:
1. Ordenaremos sus variables, las clasificaremos en niveles tal como se indicaba en la Actividad 5 y construiremos una matriz poniendo ordenadamente en la misma fila a las variables del mismo nivel.
2. Buscaremos ordenadamente en la matriz construida, comenzando por la primera fila, hasta encontrar una variable de la que no dependa ninguna otra variable de la matriz. Construiremos un subsistema con dicha variable y todas las variables de las cuáles dependa directa o indirectamente.
3. Eliminaremos de la matriz todas las variables de dicho subsistema de las que sólo dependan a lo sumo otras variables de algún subsistema ya construido.
4. Volveremos al paso 2 y repetiremos el proceso hasta que todas las variables hayan sido eliminadas de la matriz.
Ejercicio 8: obtener la descomposición máxima y la descomposición natural de los Sistemas de los Ejercicios 1 y 2. Construir los correspondientes SuperSistemas.
Actividad 14. Diremos que un Sistema Normal S=(E,c,f) es una unión de un conjunto C de Sistemas Normales Si=(Ei,ci,fi) si y sólo si:
a) E=Ui Ei
b) c=Ui ci
c) Para todo SicC, fi = f | Ei
Ahora bien, un conjunto C de Sistemas Normales pueden tener distintas uniones, en tanto que puede haber distintos comportamiento f que cumplan la condición c. Llamaremos unión realista a aquélla en que el comportamiento f viene definido por
c') f = ∩i fi* donde fi* es la extensión de fi a E, es decir que para todo xcXicE Vi , xcfi* si y sólo si existen ycfi , zcXicE-Ei Vi tal que x=(y,z)
Llamaremos sistema realista asociado a un Sistema Normal a la unión realista de su descomposición máxima. Llamaremos deconstrucción al proceso de obtención de obtención del mismo. Diremos que un Sistema Normal es reconstruible si y sólo si su sistema realista asociado es idéntico a él, es decir, si no se pierde información en el proceso de deconstrucción. En la práctica trabajaremos habitualmente con sistemas realistas, cuyo comportamiento f vendrá definido por los comportamientos de sus variables dependientes. Si un Sistema Normal no fuera reconstruible podemos introducir nuevas relaciones de dependencia directa para intentar transformarlo en reconstruible obteniendo así un sistema realista sin pérdida de información. A su vez, diremos que un Sistema Normal reconstruible (realista) es redundante si pueden eliminarse relaciones de dependencia directa sin que deje de ser reconstruible.
Un ejemplo trivial de Sistema Normal no reconstruible sería ({x,y}, Ø, (x-2)2+(y-2)2<1), cuyo proceso de deconstrucción se representa en la figura siguiente,
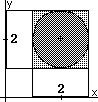
Ejercicio 9: definimos un
Sistema Normal mediante el comportamiento x2+y2+z2<1,
formado por los puntos interiores a una superficie esférica, y
la relación estructural de conexión { x→y , y→z }, siendo
x, y, z números reales. Obtener su sistema realista asociado y
representarlo gráficamente. ¿El Sistema Normal original
es reconstruible? En caso contrario, transformarlo en reconstruible
introduciendo una nueva relación de dependencia directa.
¿El nuevo Sistema obtenido será redundante?
Actividad 15. Llamaremos reducción de un Sistema Normal S=(E,c,f) a otro Sistema Normal S'=(E',c',f ') tal que
a) E' ≤ E
b) Todas las variables de entrada de S son variables de entrada de S'.
c) Todas las variables de salida de S son variables de salida de S'.
d) f ' = f | E'
Obsérvese que, a diferencia de los subsistemas, en una reducción no tiene que cumplirse c' ≤ c . Por el contrario, al eliminar variables intermedias o internas (que no sean de entrada ni de salida) puede establecerse una relación de dependencia directa en S' entre variables que en S sólo tenían una relación de dependencia indirecta.
A su vez, diremos que el Sistema Normal S es una expansión del Sistema Normal S' : para obtener una expansión introduciremos variables intermedias que nos faciliten la descomposición en subsistemas con relaciones de comportamiento más sencillas, permitiéndonos así obtener a partir dichos subsistemas la síntesis del sistema original o proyectado. Por su parte, para resolver un problema de análisis obteniendo el comportamiento global resultante de un conjunto de sistemas interconectados deberemos obtener una unión de los mismos y posteriormente llevar a cabo una reducción de la misma eliminando variables intermedias.
Ejercicio 10: obtener reducciones y en su caso expansiones de Sistemas considerados en las actividades anteriores.
Objetivos:
Actividad 16. En la Actividad 1 estudiamos cómo agrupar distintos Sistemas particulares de distinta naturaleza pero con las mismas relaciones estructurales y/o de comportamiento, que correspondían a un mismo Sistema General. La relación Sistema General-Sistemas particulares es la que corresponde, en la metodología sistémica, a la relación Teoría-Experiencia en la metodología científica tradicional. A su vez, diremos que un Sistema es un Modelo de otro Sistema cuando tienen las mismas relaciones estructurales y/o de comportamiento: podemos considerar un Sistema particular como Modelo de otro o del correspondiente Sistema General. La metodología sistémica debe permitirnos abordar diferentes problemas:
a) Dado un Sistema particular, estudiar los valores que adoptan sus distintas variables, y a partir de ello encontrar un Sistema General que reproduzca sus relaciones estructurales y de comportamiento (problema de Caja Negra).
b) Dado un conjunto de Sistemas interconectados cuyas relaciones estructurales y/o de comportamiento conocemos, obtener el comportamiento del Sistema global resultante (problema de Análisis).
c) Estudiar como interconectar un conjunto de Sistemas para reproducir un comportamiento dado de un Sistema global (problema de Síntesis).
d) Construir un Sistema (modelo) que reproduzca las relaciones estructurales y/o de comportamiento de un Sistema dado, a fin de estudiar los valores de sus variables y eventualmente su evolución (problema de Simulación).
En la práctica de la metodología sistémica es frecuente encontrar problemas mixtos respecte a los tipos indicados.
Realizar una lista de cuestiones a resolver (problemas) y clasificarlos de acuerdo con la tipología indicada.
Actividad 17. Para resolver un problema de Caja Negra, comenzaremos registrando una serie de valores de sus distintas variables (Actividad) y a continuación estudiaremos regularidades en dichos valores, bien simultáneos, bien temporalmente sucesivos. Para ello seleccionaremos ciertas posiciones temporales relativas de distintas variables (máscara) de manera que podamos encontrar en las mismas pautas que se repitan y otras que nunca aparezcan. A partir de ello formularemos la relación de comportamiento del Sistema y en su caso su relación estructural. Posteriormente, si resulta oportuno, podemos intentar resolver un problema de Síntesis para descomponer el Sistema en un conjunto de Sistemas más sencillos interconectados que nos permitan reproducir el comportamiento de la Caja Negra. Señalemos que la resolución de un problema de Caja Negra no puede considerarse definitiva, dado que el registro de nuevos valores podría obligarnos a modificar el resultado obtenido.
Veamos un ejemplo sencillo. Supongamos que tenemos dos variables, {x , s} y encontramos la siguiente evolución en el tiempo (Actividad) de las mismas:
Podemos ahora estudiar si hay alguna restricción en los valores
simultáneos, correspondiente a la máscara (x(t),s(t)). Es
fácil ver que no hay tal restricción, dado que aparecen
todos los pares posibles: (0,0), (1,0), (0,1) y (1,1). Podemos ahora
introducir algún valor posterior en la máscara, por
ejemplo (x(t),s(t),x(t+1)). En este caso, encontramos las siguientes
ternas: (0,0,1), (1,0,0), (0,1,1), (1,1,1), (0,1,0), (1,1,0), (0,0,0),
(1,0,1), es decir, las 8 posibles. Por tanto, tampoco hay ninguna
restricción. En cambio, si escogemos la máscara (x(t),
s(t), s(t+1)), únicamente aparecerán las siguientes 4
ternas: (0,0,0), (1,0,1), (0,1,1), (1,1,0). Podemos por tanto expresar
su relación de comportamiento como
Ejercicio 11: resolver el
problema de Caja Negra correspondiente a la siguiente actividad:
Actividad 18. Para resolver un problema de Síntesis de un Sistema
a) introduciremos variables intermedias,
b) obtendremos la correspondiente expansión del Sistema y a continuación
c) realizaremos su descomposición en Sistemas "elementales" del tipo que hayamos definido previamente.
El problema de Síntesis no tiene solución única, sino que depende, entre otras cosas, del repertorio de Sistemas "elementales" en que queramos descomponerlo. Y dentro de esta condición, nos interesará obtener la solución que sea "óptima" con respecto a determinados criterios (por ejemplo, haciendo mínimo el número de Sistemas elementales a utilizar o el número de sus conexiones). La manera de hacer todo esto dependerá del tipo de Sistemas "elementales" deseado. Por ejemplo, si trabajamos con Sistemas "elementales" con una única variable dependiente (de salida), deberemos realizar la descomposición máxima.
Si las variables son booleanas (es decir, sólo tienen 2 valores, 1 y 0 o verdadero y falso), podemos descomponerlos fácilmente en un número reducido de sistemas booleanos:
Podemos obtener una descomposición de un sistema booleano
mediante un sumatorio para cada variable dependiente, a partir de la
tabla que lo define, tomando un sumando para cada fila en la que dicha
variable tenga el valor 1, el cuál lo obtendremos multiplicando
los valores de las
variables de las que depende, directamente si en la fila tiene el valor
1, o su negación si tiene el valor 0. Por ejemplo, la primera
relación de comportamiento obtenida en la Actividad 17 la
podríamos expresar así:
Si tenemos definida congruentemente una medida sobre el conjunto de valores Vy de la variable dependiente y, m:Vy→R+, llamaremos grado de acoplamiento relativo ρy de dicha variable y entre el Modelo y el Sistema Real para unas Actividades de los mismos al cociente entre su grado de acoplamiento y el promedio de la medida del valor de y en el Sistema Real en la correspondiente Actividad del mismo, ρy=δy/μ(m(y)). El grado de ajuste relativo ρ del comportamiento del Modelo al Sistema Real para dichas Actividades será el promedio de los grados de acoplamiento relativo para todas las variables dependientes.
Ejercicio 17: calcular el grado de ajuste y el grado de ajuste relativo del Modelo obtenido en el Ejercicio 14 (u otro).
Objetivos:
Actividad 23. Una variable aleatoria (X) en un conjunto-población es cualquier variable que puede tener distintos valores (x) para los distintos elementos-individuos de la población. La distribución estadística de dichos valores no tiene en cuenta los individuos concretos para los que dicha variable tiene cada valor, sino cuántos la tienen, a lo que llamamos frecuencia de dicho valor en la población. Llamaremos parámetro poblacional a cualquier cantidad que sólo dependa de las frecuencias. Para caracterizar una distribución estadística, nos interesará conocer su centralidad, dada por un valor alrededor del cuál se agrupan los valores de la variable aleatoria, y su dispersión, para expresar el alejamiento de dichos valores entre sí.
Como medidas de centralidad podemos tomar:
La moda: aquel valor que tenga la máxima frecuencia en la población.
La mediana: suponiendo que el conjunto de valores de la variable aleatoria esté ordenado, será un valor que tenga tantos individuos con un valor inferior como con un valor superior.
La media μ(X): suponiendo que los valores de la variable aleatoria sean cantidades sumables, y que el tamaño (número de individuos) de la población sea finito, viene dada por la suma de los valores para todos los individuos de la població dividida por su tamaño.
Como medidas de dispersión podemos tomar:
Los cuartiles primero y tercero: suponiendo que el conjunto de valores de la variable aleatoria esté ordenado, los cuartiles serán tres valores que dividan al conjunto de valores en cuatro subconjuntos de valores que correspondan al mismo número de individuos; obsérvese que el segundo cuartil coincidirá con la mediana. Si tenemos definida una distancia en el conjunto de valores, podemos medir la dispersión como la distancia entre el primer y el tercer cuartil.
La amplitud: suponiendo que además tengamos definida una distancia en el conjunto de valores, será la distancia entre los valores mínimo y máximo en la población.
La desviación media: suponiendo que los valores de la variable aleatoria sean cantidades sumables, y que el tamaño de la población sea finito, será la media del valor absoluto de las diferencias entre su valor para cada individuo y su valor medio
La varianza σ2(X): suponiendo que los valores de la variable aleatoria sean cantidades sumables, y que el tamaño de la población sea finito, será la media del cuadrado de las diferencias entre su valor para cada individuo y su valor medio [σ2(X)=μ((X-μ(X))2)]. La varianza puede calcularse también como la media de los cuadrados menos el cuadrado de la media [σ2(X)=μ(X2)-μ(X)2] . Para calcularla de esta forma, y en el caso de que la media sea mucho mayor que la amplitud, conviene restar a todos los valores una cantidad fija próxima a su valor mínimo, operación que no modificará la dispersión.
La desviación típica σ(X): es la raiz cuadrada de la varianza.
Llamaremos normalización de una variable al resultado de restarle su media y dividir la diferencia por su desviación típica, N(X)=(X-μ(X))/σ(X) ; la media de la variable normalizada valdrá cero [μ(N(X))=0] y su desviación típica valdrá uno [σ(N(X))=1].
Ejercicio 18: definir una variable aleatoria (por ejemplo, el número de calzado) en la población definida por los alumnos de la asignatura, y obtener todos los parámetros poblacionales definidos en esta actividad. Estudiar cómo simplificar el cálculo de algunos de ellos utilizando las frecuencias.
Actividad 24. Llamaremos probabilidad de un subconjunto de valores de una variable aleatoria al cociente entre el número de individuos que tienen alguno de los valores del subconjunto y el tamaño de la población. Si el conjunto de valores es finito, podremos calcular la probabilidad de cada valor como su frecuencia dividida por el tamaño de la población, y la probabilidad de un subconjunto de valores como la suma de las probabilidades de cada uno de ellos. En tal caso, la suma de las probabilidades de todos los valores será igual a 1: llamaremos distribución probabilística a cualquier aplicación que asigne un número real no negativo a cada valor de un conjunto de valores tal que su suma valga 1. Si el conjunto de valores no es finito, pero tenemos definida una medida sobre el mismo, llamaremos distribución de densidad probabilística a cualquier aplicación que asigne un número real no negativo a cada valor tal que su integral valga 1: la probabilidad de un subconjunto de valores vendrá dada por la integral de dicha aplicación sobre el mismo.
Ejercicio 19: estudiar cómo obtener la media de una variable aleatoria conociendo su distribución probabilística. Aplicarlo al caso del Ejercicio 18. ¿Cómo podríamos definir la media de una distribución de densidad probabilística?
Actividad 25: Si trabajamos con dos variables aleatorias X,Y combinadas, podemos obtener del mismo modo la probabilidad (absoluta) P(x,y) de que dichas variables tengan simultáneamente unos valores determinados contando el número de individuos en que ello se produzca y dividiéndolo por el tamaño de la población. Pero en determinadas ocasiones nos interesará conocer la probabilidad condicional, P(y|x), definida como la probabilidad de un valor (y) de una variable (Y) restringida a la subpoblación definida por un determinado valor (x) de otra variable (X). Para ello podemos contar el número de individuos que tienen el par de valores (x.y) y dividirlo por el número de individuos que tienen el valor (x) de la segunda variable, que será el tamaño de la subpoblación. Pero podemos también calcular la probabilidad condicional utilizando el Teorema de Bayes, que nos dice que P(y|x)=P(x,y)/P(x) . Si las dos variables aleatorias son independientes, la probabilidad condicional coincidirá con la probabilidad absoluta del valor de la primera variable, P(y|x)=P(y), y se cumplirá que P(x,y)=P(x)P(y) .
Ejercicio 20: combinar la variable aleatoria estudiada en el Ejercicio 18 con otra variable definida en el conjunto de alumnos de la asignatura (por ejemplo, el sexo o la edad). Obtener las probabilidades condicionadas de la primera variable respecto de la segunda. ¿Son independientes? A partir de la probabilidades ya calculadas, y fijando el valor de la primera variable, obtener la probabilidad condicional de la segunda variable respecto de dicho valor.
Ejercicio 21: en una ciudad multiétnica se comete un delito. Un testigo afirma que dicho delito ha sido cometido por una persona "de color". Pero reproduciendo la situación en las mismas condiciones de iluminación se encuentra que el testigo acierta el "color" en un 70% de los casos, tanto si es realmente "de color" como "blanca". Sabiendo que en la ciudad hay un 10% de personas "de color", calcular cuál es la probabilidad de que el delito haya sido cometido realmente por una persona "de color".
Actividad 26. Llamamos muestra (sin reemplazamiento) de una población a cualquier subconjunto de la misma. Una muestra con reemplazamiento se obtendrá extrayendo sucesivamente individuos de la población sin suprimirlos de la misma. Llamamos estadístico a cualquier parámetro poblacional restringido a una muestra, como la media muestral ¯X o la desviación típica muestral s(X) [naturalmente, para los estadisticos se cumplen la mismas relaciones que para los parámetros poblacionales correspondientes, por ejemplo s2(X)=¯(X2)-(¯X)2 ]. Y llamamos distribución muestral a la distribución de un estadístico en el conjunto de todas las muestras de la población de un cierto tamaño n. Los parámetros poblacionales de la distribución muestral, como la media de las medias μ(¯X), la varianza de las medias σ2(¯X) o la media de las varianzas μ(s2(X)), son importantes para realizar estimaciones a partir del estadístico de una muestra sobre el correspondiente parámetro poblacional. A tal efecto, hay que tener en cuenta las siguientes relaciones:
μ(¯X)=μ(X)
σ2(¯X)=σ2(X)/n si las muestras son con reemplazamiento o la población es infinita (aproximadamente, si es muy grande).
μ(s2(X))=σ2(X)·(n-1)/n
Diremos que un estadístico es insesgado cuando la media de su distribución muestral es igual al correspondiente parámetro poblacional. Para estimar un parámetro poblacional a partir de un estadístico, éste debe ser insesgado.
Ejercicio 22: ¿la media y la varianza muestrales son estadísticos insesgados? En caso de que alguna de ellas no lo sea, ¿cómo podríamos obtener un estadístico corregido que sí fuera insesgado? Tomando el conjunto de alumnos de la asignatura como una muestra del conjunto de alumnos de la licenciatura, realizar una estimación sobre este conjunto de la media y de la varianza de la variable aleatoria del Ejercicio 18. Estimar también la varianza de la distribución muestral de las medias.
Actividad 27. Diremos que [S1,S2] es un intervalo de confianza del 100α% para un parámetro poblacional Ω si la probabilidad de que Ω se encuentre en dicho intervalo es igual a α. Para poder obtener intervalos de confianza necesitaremos conocer la distribución muestral de un estadístico insesgado S de dicho parámetro poblacional.
Definimos la distribución normal como la distribución de densidad probabilística dada por la fórmula
Actividad 28. Si la distribución de una variable aleatoria X en una población infinita se ajusta a una distribución normal, la distribución muestral del estadístico
Objetivos:
Actividad 32. Norbert Wiener (1948) definió la Cibernética como la ciencia de la comunicación y el control en el hombre, el animal y la máquina. Aquí "comunicación" hace referencia al intercambio de información entre un Sistema y su entorno, y "control" hace referencia a la realización de las acciones necesarias para obtener los resultados deseados: llamaremos Sistema Cibernético (y también "Sistema con objetivo" o "Sistema controlador") a un Sistema capaz de modificar sus respuestas a partir de la información recibida a fin de alcanzar un objetivo:

Objetivos:
Si podemos estimar la probabilidad de una variable objetivo (y) condicionada al escenario y la estrategia, P(y|s,e), así como la probabilidad de los distintos escenarios, P(s), supuestos independientes de las estrategias, aplicando el Teorema de Bayes obtendremos
Actividad 37. Los algoritmos genéticos permiten simular la selección natural para escoger la mejor opción. Para ello se dan valores aleatorios a las variables de entrada, tanto las no controlables como las de control, modificando en cada paso las probabilidades de los valores de las variables de control en función de los resultados obtenidos. Ello puede hacerse de diversas formas. Por ejemplo, podría utilizarse un modelo de refuerzo lineal como el que se describe en la Actividad 35. Podría también tomarse en cada caso una probabilidad igual a la de la satisfacción obtenida. Y podría seleccionarse en cada paso un determinado porcentaje de los valores que han generado los mejores resultados.
Ejercicio 37: aplicar un algoritmo genético en las condiciones del Ejercicio 35, partiendo de 100 casos con estrategia 1, 100 casos con estrategia 2 y 100 casos con estrategia 3, y seleccionando en cada caso el 50% (o su parte entera) con mejores resultados (probabilidad de conseguir el objetivo). Para determinar de cada estrategia cuántos se encuentran en cada escenario, tomar la parte proporcional aproximando si es necesario con la parte entera y el resto mayor, o al azar en caso de restos iguales. En caso de empates con resultados seleccionables, tomar para cada estrategia la parte proporcional, aproximando del mismo modo si es necesario. ¿Cuántos habrán sobrevivido de cada estrategia después de 4 pasos?
Actividad 38. Para obtener por muestreo una solución que esté entre los 100p% mejores con una probabilidad del 100α%, deberemos calcular cual es la probabilidad de que entre n casos no haya ninguno que esté entre los 100p% mejores. Dado que la probabilidad de que un caso no esté entre los 100p% mejores es 1-p, y que los distintos casos deben considerarse independientes, la probabilidad de que entre n casos no haya ninguno que esté entre los 100p% mejores será (1-p)n. Por lo tanto, la probabilidad de que entre n casos haya alguno que esté entre los 100p% mejores será α=1-(1-p)n.
Ejercicio 38: ¿de qué tamaño deberá ser la muestra (con reemplazamiento) para garantizar con una probabilidad del 90% que el mejor resultado de la muestra esté entre el 5% de los mejores?
Objetivos:
Específicos:
1. Comprender los conceptos fundamentales de la Teoría General de Sistemas.
2. Aprender a utilizar algunas herramientas básicas de la metodología sistémica.
3. Adquirir o actualizar nociones básicas de Estadística.
4. Aprender a realizar simulaciones construyendo modelos cibernéticos.
5. Adquirir técnicas para encontrar la solución óptima a un problema.
6. Estudiar el comportamiento de sistemas caóticos.
Genéricos:
- Aprender a trabajar en equipo.
- Aprender a exponer públicamente un trabajo.
- Adquirir respeto por l@s compañer@s que exponen un trabajo, atendiéndoles y ayudàndoles en caso necesario.
- Aprender a redactar una memoria sobre una materia o un trabajo realizado..
- Adquirir la capacidad de cuestionar la fiabilidad de los resultados obtenidos.
Metodología:
- Trabajo en clase en grupos pequeños, realizando actividades y resolviendo ejercicios, seguido de su exposición pública.
- Trabajo pràctico en aula de informàtica, construyendo modelos para la simulación de problemas determinados.
- Trabajo individual y en equipo fuera de clase, elaborando memorias para su presentación al profesor.
Bibliografía:
Genérica:
- Ashby,W.R. (1958), Requisite Variety and its implications for
the Control of Complex Systems, en Cybernetica 1:2, p.83.99
(disponible en http://pcp.vub.ac.be/Books/AshbyReqVar.pdf,
republicado en la web por F.Heylighen-Principio Cybernetica Project).
- Bertalanffy,L.V. (1976), Teoría general
de los sistemas, Fondo de Cultura Económica,
México.
- Caselles, A. (1984), A Method to Compare Theories in the Light
of General Systems Theory, en Cybernetics
and Systems Research 2, R.Trappl ed., North-Holland, Amsterdam,
pp.27-32.
- Caselles, A. (1992), Structure and Behavior in General Systems Theory, en Cybernetics and Systems: An International Journal, 23, pp.549-560.
- Caselles, A. (1993), Systems Decomposition and coupling, en Cybernetics and Systems: An International Journal, 24, pp.305-323.
- Caselles, A. (2008), Modelización y simulación de
sistemas complejos, Universitat de València
- Forrester,J.W. (1968), Principles of Systems, Wright-Allen, Cambridge, USA.
- George,F.H. (1968), Cibernética y biología, Alhambra, Madrid.
- Guillaumaud,J. (1971), Cibernética y lógica dialéctica, Artiach, Madrid.
- Klir,J. & Valach,M. (1967), Cybernetic Modelling, Iliffe Books, London.
- Klir,G.J. (ed.) y otros (1978), Tendencias en la teoría general de sistemas, Alianza Universidad, Madrid
- Klir,G.J. (1980), Teoría General de Sistemas, ICE, Madrid.
- Klir,G.J. & Parviz,B (1992), Possibility-Probability conversions: An Empirical Study, en Cybertics and Systems Research, R.Trappl ed., vol.1, pp.19-26, World Scientific, Singapore.
- Klir,G.J. & Parviz,B (1994), On Conditional Possibilities: An
Experimental Study, en Cybernetics
and Systems'94, R.Trappl ed., vol.I, pp.11-17, World Scientific,
Singapore.
- Laszlo,E. (1981), Defensa de la filosofía de sistemas, en Hacia una filosofía de sistemas, Cuadernos Teorema, València.
- Mesarovic,M.D. & Takahara,Y. (1975), General Systems Theory: Mathematical Foundations, Academic Press, New York.
- Piaget,J. (1969), Biología y conocimiento, siglo XXI de EspaÑa, Madrid.
- Shannon,C.E. & Weaver,W. (1949), The Mathematical Theory of Communication, Univ. of Illinois Press, Urbana, USA.
- Pla-Lopez,R. (2001), Adaptive Systems, en Systems Sciences and Cybernetics, editado por Francisco Parra-Luna en Encyclopedia of Life Suport Systems (EOLSS), Eolss Publishers, Oxford, U.K., http://www.eolss.net/
- Turing,A.M. (1974), ¿Puede pensar una máquina?, Cuadernos Teorema, València.
- Wiener,N. (1961), Cibernética, Guadiana, Madrid.
Específica:
Instrumentos informáticos (SIGEM, REGINT, EXTRAPOL) diseñados por Antonio Caselles que pueden encontrarse en la sección de Recursos del Aula Virtual de la asignatura, incluyendo un Manual del SIGEM. SIGEM (SIstema GEnerador de Models) para octave, versión 1.1
- Seguimiento de la actividad realizada en clase, incluyendo la exposición pública de los resultados obtenidos.
- Presentación de una memoria individual recopilando los contenidos de la asignatura trabajados en clase, sobre la base de una asistencia regular a la misma.
- Presentación de una memoria de un trabajo en equipo sobre un problema de simulación
- Complementariamente, y en caso de falta de asistencia regular o falta de información sobre la actividad realizada en clase, podrá realizarse un examen individual escrito sobre los temas correspondientes.
Objetivos:
- Estudiar las analogías estructurales entre objetos y procesos de diferente naturaleza, introduciendo así el concepto de Sistema General.
- Estudiar distintas formas de relaciones entre distintos objetos o variables.
- Buscar una definición general de Sistema que permita tomar en consideración los distintos tipos de relaciones.
- Introducir la evolución en el tiempo, y con ello el
concepto de Sistema Dinámico y
Sistema Secuencial.
- Introducir la noción de Sistemas no deterministas (Estocásticos o Borrosos).
- Entender la diferencia entre un bucle en una relación de dependencia y una retroacción en la evolución temporal de una variable.
- Estudiar el acoplamiento
y descomposición de
Sistemas.
Actividad 1: Agrupar de 2 en 2 los siguientes Sistemas, estableciendo correspondencias entre sus componentes de manera que sus relaciones coincidan:
- Según la Ley de Ohm, la intensidad de la corriente eléctrica a lo largo de un conductor es igual a la diferencia de potencial entre sus extremos dividido por su resistencia.
- Las estaciones del año son Primavera, Verano, Otoño e Invierno, y vuelta a empezar.
- Si cada año un alumno duplica sus conocimientos, diremos que es un buen estudiante.
- Según la Ley de Lenz, si movemos un conductor en un campo magnético se genera una corriente eléctrica cuyos efectos tienden a contrarrestar el campo magnético.
- Los beneficios obtenidos por una empresa pueden utilizarse para incrementar la producción o para renovar la tecnología.
- Si separamos a la población en grupos con el mismo nivel de renta, encontramos que en aquéllos que tienen doble, triple, etc. renta el porcentaje de votos a un determinado partido es la mitad, la tercera parte, etc., respectivamente.
- El funcionamiento del corazón pasa por las fases de sístole auricular, sístole ventricular, diástole ventricular, diástole general y de nuevo sístole auricular.
- Conectamos 4 conductores de manera que por dos de ellos pase la misma intensidad de corriente eléctrica, y los otros dos estén sometidos a la misma diferencia de potencial; todos los conductores se mantienen a la misma temperatura.
- Para saber cuántas unidades podemos comprar de un producto necesitamos conocer el dinero de que disponemos y el precio de cada unidad.
- Según la Ley de Le Chatelier, si durante una reacción química reversible modificamos sus condiciones, el equilibrio se desplazará para compensar, en sentido contrario, dicha modificación.
- El tamaño de una población se va alterando en función de los nacimientos y defunciones que se produzcan.
- Los fondos que se destinen a "cañones" y a "mantequilla" tienen el límite del presupuesto disponible.
- La proporción de enfermos que responden favorablemente a un tratamiento es inversamente proporcional a su edad.
- De acuerdo con un convenio entre ellos, en los países A, B, C y D el litro de leche tiene el mismo precio; pero en cambio sólo A y B comparten el precio del pan, y sólo C y D comparten el precio del arroz.
- El stock en un almacén aumenta por la entrada de productos y disminuye por las ventas.
- El planeta está condenado si la humanidad multiplica por 2 cada década su consumo de energía.
Actividad 3: llamamos relaciones estructurales a las que se dan entre los elementos de un Sistema considerados como objetos singulares, indicando su conexión o dependencia; llamamos relaciones de comportamiento a las que se dan entre los conjuntos de valores de los distintos elementos de un Sistema considerados como variables, indicando la compatibilidad entre dichos valores.
Analizar qué relaciones son estructurales y cuáles son de comportamiento en las actividades anteriores.
Actividad 4: estudiar cómo dar una definición formal de Sistema de modo que puedan tomarse en consideración relaciones tanto estructurales como de comportamiento. Pueden tenerse en cuenta a tal efecto las definiciones siguientes, en las que ≤ indica una relación de inclusión, X indica un producto cartesiano, U indica una unión de conjuntos, P indica el conjunto de los subconjuntos de un conjunto y Ø es el conjunto vacío.
S≤ XicI Vi (Mesarovic&Takahara 1975)
S=(E,R) tal que ØcR≤P(UncN (E n)) (Yang 1989)
S=(E,R) tal que ØcR≤Tm tal que Tm+1=P( UncN (Tm) n ), T0=E (Caselles 1993)
S=(I, {Vi}icI, R) tal que R ≤ P(Un=1...m I n) U P(XicI Vi) (Pla 2007)
Actividad 5. Llamaremos Sistema de conexiones a un Sistema con una relación estructural binaria, R ≤ EXE, de modo que (a,b)cR si y sólo si a depende directamente de b, b→a. Diremos de un Sistema de conexiones que es jerárquico si en él no pueden encontrarse bucles, de manera que un elemento no pueda depender directa ni indirectamente de sí mismo. En tal caso, si el número de elementos es finito, habrá necesariamente un subconjunto de elementos que no dependan de ningún otro, a los cuáles llamaremos elementos de nivel 1 o de entrada. Asimismo, diremos que un elemento es de nivel n>1 si y sólo si depende de algún elemento de nivel n-1 y en todo caso de elementos de nivel inferior. Llamaremos elementos de salida a aquéllos de los que no depende ningún otro.
Para establecer una clasificación en niveles comenzaremos extrayendo sus elementos de entrada (nivel 1). A continuación prescindiremos de ellos y buscaremos cuáles serían de entrada entre los restantes (nivel 2), y así sucesivamente. El Sistema será jerárquico si y sólo si a través de este proceso podemos llegar a clasificar en niveles todos sus elementos. El Sistema será conexo si no tiene elementos aislados, es decir si todos sus elementos tienen una relación de dependencia con algún otro.
Ejercicio 1: estudiar si es jerárquico el siguiente Sistema de conexiones, clasificando en niveles sus elementos:
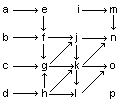
Estudiar en qué casos cambiando
el sentido de una única flecha el Sistema deja de ser
jerárquico.
Actividad 6. Llamaremos Sistema Normal a un Sistema S={E,c,f}, tal que E es un conjunto de variables, c≤ EXE es una relación estructural de conexión jerárquica y f ≤ XicE Vi es una relación de comportamiento.
Poner ejemplos de Sistemas Normales, especificando E, {Vi}icE, c y f .
Analizar en qué casos la relación estructural c podría inferirse de la relación de comportamiento f :
Ejercicio 2: dada la relación de comportamiento definida por u=x2+y2 , v=y2-z2, w=u2+v2, siendo x, y, u, v, w números reales, inferir de ella una relación estructural para definir un Sistema Normal.
Actividad 7. Llamaremos Sistema Temporal a un sistema con alguna relación de comportamiento que involucra alguna variable temporal X cuyo conjunto de valores es VX ≤ DXT = {x / x:T→DX}, es decir, un conjunto de aplicaciones de T en un dominio DX, siendo T un intervalo temporal.
Analizar cuáles de los Sistemas anteriormente considerados son Temporales.
Actividad 8. Llamaremos Sistemas Dinámicos a aquellos Sistemas Temporales cuyas relaciones de comportamiento pueden describirse clasificando sus variables en variables de entrada X, variables de salida Y y variables de estado U, de modo que:
a) La evolución en el tiempo de las variables de salida Y a partir de un instante tcT depende del valor de las variables de estado U en el instante t y de la evolución en el tiempo de las variables de entrada X a partir de dicho instante t.
b) El valor de las variables de estado U en un instante tcT depende del valor de las mismas en cualquier instante t'≤t y de la evolución en el tiempo de las variables de entrada X entre los instantes t' y t, de modo que se cumplan las propiedades de
b1) Identidad: si t'=t, el valor de las variables de estado U en los instantes t' y t debe coincidir.
b2) Transitividad: si t"≤t'≤t, para una determinada evolución en el tiempo de las variables de entrada X entre los instantes t" y t, la dependencia del valor de las variables de estado U en el instante t a partir de su valor en el instante t" debe ser equivalente a la que se derivaría del valor de dichas variables en el instante t' dependientes de su valor en el instante t.


Poner ejemplos de Sistemas Dinámicos Deterministas, Estocásticos y Borrosos e intentar definir sus relaciones.
Actividad 9. Un Sistema Dinámico no anticipatorio será aquél en que los valores de las variables de salida Y no dependan de valores posteriores de las variables de entrada X. Una forma sencilla de Sistemas Dinámicos Deterministas no anticipatorios con intervalo temporal discreto son los Sistemas Secuenciales, cuyas relaciones de comportamiento vienen dadas por
y(t) = F(x(t),u(t))
u(t+1)=G(x(t),u(t))
donde x, u, y pueden representar tuplas de variables de entrada, estado y salida, respectivamente. Es decir, y(t)=(y1(t),y2(t),y3(t)...), etc.
Ejercicio 3: dado un Sistema Secuencial definido por y(t)=u(t)·x(t), u(t+1)=u(t)+x(t), expresar y(5) como función del estado inicial u(0) y de la secuencia de valores de entrada (x(0),x(1),x(2),x(3),x(4),x(5)).
Tomando como elementos los valores de x(t), u(t), y(t) para t=0,1,2,3,4,5, analizar si su Sistema de conexiones es jerárquico, clasificando en niveles dichos elementos.
Llamaremos retroacción a la situación que se da cuando el valor de una variable depende directa o indirectamente de valores anteriores de la misma ¿En un Sistema Secuencial se produce retroacción? ¿Hay bucles en su sistema de conexiones?
Actividad 10. Diremos que un Sistema Normal S'=(E',c',f ') es un subsistema del Sistema Normal S=(E,c,f) si y sólo si:
a) E' ≤ E
b) c' ≤ c
c) f ' = f | E', es decir, f ' es la restricción de f a E' , es decir que para todo xcXicE ' Vi , xcf ' si y sólo si existe ycXicE-E ' Vi tal que (x,y)cf .
d) Si un elemento de E' no es de entrada en S', c' incluye todas las dependencias directas sobre el mismo. Es decir, que para todo i,j,kcE, si (i,j)cc' y (i,k)cc, entonces (i,k)cc' (lo que supone que kcE').
Ejercicio 4: extraer subsistemas del Sistema de conexiones del Ejercicio 1.
Ejercicio 5: extraer subsistemas del Sistema Normal obtenido en el Ejercicio 2, indicando cuáles serían sus relaciones de comportamiento.
Actividad 11. Dados dos subsistemas A, B de un Sistema Normal, diremos que B depende directamente de A, A→B, si y sólo si existe alguna variable de entrada de B que sea variable dependiente (no de entrada) de A.
Dado un conjunto C de subsistemas de un Sistema Normal, llamaremos SuperSistema del mismo al Sistema de conexiones SS=(C,R), tal que R≤CXC es una relación estructural binaria formada por todos los pares (B,A) tales que A→B . Diremos que dicho SuperSistema está bien determinado si y sólo si es jerárquico.
Ejercicio 6: dados los conjuntos de subsistemas obtenidos en los Ejercicios 4 y 5, obtener sus correspondientes SuperSistemas y estudiar si están o no bien determinados.
Actividad 12. Diremos que un conjunto de subsistemas Si de un Sistema Normal S es una descomposición del mismo si y sólo si:
a) El SuperSistema correspondiente está bien determinado.
b) Ninguna variable es dependiente en más de un subsistema.
c) Toda variable del Sistema Normal S es una variable de alguno de sus subsistemas, es decir Ui Ei = E .
Ejercicio 7: estudiar si los conjuntos de subsistemas obtenidos en los Ejercicios 4 y 5 son una descomposición de un Sistema Normal; estudiar cómo podríamos obtener una descomposición de un Sistema Secuencial.
Actividad 13. Llamaremos descomposición máxima de un Sistema Normal a la formada por los subsistemas resultantes de tomar cada variable dependiente o de salida y las variables de las cuáles depende directamente junto con dichas dependencias directas. Llamaremos descomposición natural de un Sistema Normal con un conjunto finito de variables al resultante de aplicarle el Algoritmo 1:
1. Ordenaremos sus variables, las clasificaremos en niveles tal como se indicaba en la Actividad 5 y construiremos una matriz poniendo ordenadamente en la misma fila a las variables del mismo nivel.
2. Buscaremos ordenadamente en la matriz construida, comenzando por la primera fila, hasta encontrar una variable de la que no dependa ninguna otra variable de la matriz. Construiremos un subsistema con dicha variable y todas las variables de las cuáles dependa directa o indirectamente.
3. Eliminaremos de la matriz todas las variables de dicho subsistema de las que sólo dependan a lo sumo otras variables de algún subsistema ya construido.
4. Volveremos al paso 2 y repetiremos el proceso hasta que todas las variables hayan sido eliminadas de la matriz.
Ejercicio 8: obtener la descomposición máxima y la descomposición natural de los Sistemas de los Ejercicios 1 y 2. Construir los correspondientes SuperSistemas.
Actividad 14. Diremos que un Sistema Normal S=(E,c,f) es una unión de un conjunto C de Sistemas Normales Si=(Ei,ci,fi) si y sólo si:
a) E=Ui Ei
b) c=Ui ci
c) Para todo SicC, fi = f | Ei
Ahora bien, un conjunto C de Sistemas Normales pueden tener distintas uniones, en tanto que puede haber distintos comportamiento f que cumplan la condición c. Llamaremos unión realista a aquélla en que el comportamiento f viene definido por
c') f = ∩i fi* donde fi* es la extensión de fi a E, es decir que para todo xcXicE Vi , xcfi* si y sólo si existen ycfi , zcXicE-Ei Vi tal que x=(y,z)
Llamaremos sistema realista asociado a un Sistema Normal a la unión realista de su descomposición máxima. Llamaremos deconstrucción al proceso de obtención de obtención del mismo. Diremos que un Sistema Normal es reconstruible si y sólo si su sistema realista asociado es idéntico a él, es decir, si no se pierde información en el proceso de deconstrucción. En la práctica trabajaremos habitualmente con sistemas realistas, cuyo comportamiento f vendrá definido por los comportamientos de sus variables dependientes. Si un Sistema Normal no fuera reconstruible podemos introducir nuevas relaciones de dependencia directa para intentar transformarlo en reconstruible obteniendo así un sistema realista sin pérdida de información. A su vez, diremos que un Sistema Normal reconstruible (realista) es redundante si pueden eliminarse relaciones de dependencia directa sin que deje de ser reconstruible.
Un ejemplo trivial de Sistema Normal no reconstruible sería ({x,y}, Ø, (x-2)2+(y-2)2<1), cuyo proceso de deconstrucción se representa en la figura siguiente,

donde el sombreado oscuro representa el
comportamiento del sistema original y se han remarcado sobre los ejes
sus restricciones sobre las variables x
e y, indicándose con un
sombreado más claro las zonas añadidas en su unión
realista. Para transformar el sistema original en reconstruible
(realista) bastaría con introducir una relación de
dependencia x→y .
Actividad 15. Llamaremos reducción de un Sistema Normal S=(E,c,f) a otro Sistema Normal S'=(E',c',f ') tal que
a) E' ≤ E
b) Todas las variables de entrada de S son variables de entrada de S'.
c) Todas las variables de salida de S son variables de salida de S'.
d) f ' = f | E'
Obsérvese que, a diferencia de los subsistemas, en una reducción no tiene que cumplirse c' ≤ c . Por el contrario, al eliminar variables intermedias o internas (que no sean de entrada ni de salida) puede establecerse una relación de dependencia directa en S' entre variables que en S sólo tenían una relación de dependencia indirecta.
A su vez, diremos que el Sistema Normal S es una expansión del Sistema Normal S' : para obtener una expansión introduciremos variables intermedias que nos faciliten la descomposición en subsistemas con relaciones de comportamiento más sencillas, permitiéndonos así obtener a partir dichos subsistemas la síntesis del sistema original o proyectado. Por su parte, para resolver un problema de análisis obteniendo el comportamiento global resultante de un conjunto de sistemas interconectados deberemos obtener una unión de los mismos y posteriormente llevar a cabo una reducción de la misma eliminando variables intermedias.
Ejercicio 10: obtener reducciones y en su caso expansiones de Sistemas considerados en las actividades anteriores.
Objetivos:
- Aprender a contrastar un Sistema General con Sistemas particulares.
- Obtener las relaciones de comportamiento y estructural que corresponden a la actividad observada de un Sistema.
- Reproducir el comportamiento de un Sistema conectando Sistemas
más sencillos.
- Obtener el comportamiento global de un conjunto de Sistemas interconectados.
- Entender cómo utilizar un Sistema para simular el
comportamiento de otro.
Actividad 16. En la Actividad 1 estudiamos cómo agrupar distintos Sistemas particulares de distinta naturaleza pero con las mismas relaciones estructurales y/o de comportamiento, que correspondían a un mismo Sistema General. La relación Sistema General-Sistemas particulares es la que corresponde, en la metodología sistémica, a la relación Teoría-Experiencia en la metodología científica tradicional. A su vez, diremos que un Sistema es un Modelo de otro Sistema cuando tienen las mismas relaciones estructurales y/o de comportamiento: podemos considerar un Sistema particular como Modelo de otro o del correspondiente Sistema General. La metodología sistémica debe permitirnos abordar diferentes problemas:
a) Dado un Sistema particular, estudiar los valores que adoptan sus distintas variables, y a partir de ello encontrar un Sistema General que reproduzca sus relaciones estructurales y de comportamiento (problema de Caja Negra).
b) Dado un conjunto de Sistemas interconectados cuyas relaciones estructurales y/o de comportamiento conocemos, obtener el comportamiento del Sistema global resultante (problema de Análisis).
c) Estudiar como interconectar un conjunto de Sistemas para reproducir un comportamiento dado de un Sistema global (problema de Síntesis).
d) Construir un Sistema (modelo) que reproduzca las relaciones estructurales y/o de comportamiento de un Sistema dado, a fin de estudiar los valores de sus variables y eventualmente su evolución (problema de Simulación).
En la práctica de la metodología sistémica es frecuente encontrar problemas mixtos respecte a los tipos indicados.
Realizar una lista de cuestiones a resolver (problemas) y clasificarlos de acuerdo con la tipología indicada.
Actividad 17. Para resolver un problema de Caja Negra, comenzaremos registrando una serie de valores de sus distintas variables (Actividad) y a continuación estudiaremos regularidades en dichos valores, bien simultáneos, bien temporalmente sucesivos. Para ello seleccionaremos ciertas posiciones temporales relativas de distintas variables (máscara) de manera que podamos encontrar en las mismas pautas que se repitan y otras que nunca aparezcan. A partir de ello formularemos la relación de comportamiento del Sistema y en su caso su relación estructural. Posteriormente, si resulta oportuno, podemos intentar resolver un problema de Síntesis para descomponer el Sistema en un conjunto de Sistemas más sencillos interconectados que nos permitan reproducir el comportamiento de la Caja Negra. Señalemos que la resolución de un problema de Caja Negra no puede considerarse definitiva, dado que el registro de nuevos valores podría obligarnos a modificar el resultado obtenido.
Veamos un ejemplo sencillo. Supongamos que tenemos dos variables, {x , s} y encontramos la siguiente evolución en el tiempo (Actividad) de las mismas:
| t |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
| x |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
| s |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
|
que expresaría una relación estructural de dependencia de s(t+1) respecto de x(t) y s(t) . |
| t |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
| x |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
| s |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
| y |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
Actividad 18. Para resolver un problema de Síntesis de un Sistema
a) introduciremos variables intermedias,
b) obtendremos la correspondiente expansión del Sistema y a continuación
c) realizaremos su descomposición en Sistemas "elementales" del tipo que hayamos definido previamente.
El problema de Síntesis no tiene solución única, sino que depende, entre otras cosas, del repertorio de Sistemas "elementales" en que queramos descomponerlo. Y dentro de esta condición, nos interesará obtener la solución que sea "óptima" con respecto a determinados criterios (por ejemplo, haciendo mínimo el número de Sistemas elementales a utilizar o el número de sus conexiones). La manera de hacer todo esto dependerá del tipo de Sistemas "elementales" deseado. Por ejemplo, si trabajamos con Sistemas "elementales" con una única variable dependiente (de salida), deberemos realizar la descomposición máxima.
Si las variables son booleanas (es decir, sólo tienen 2 valores, 1 y 0 o verdadero y falso), podemos descomponerlos fácilmente en un número reducido de sistemas booleanos:
Disyunción
o suma:
|
Conjunción
o producto:
|
Negación:
|
A los que habría que añadir un elemento de retardo si queremos construir Sistemas dinámicos o temporales: x(t+1) = x(t)
|
s(t+1) = x(t)·~s(t) +
~x(t)·s(t)
Actividad 22. Para la
validación de un Modelo es necesario compararlo con los Sistemas
Reales que pretende simular. Si el Modelo y el Sistema Real comparten
el conjunto de variables, podremos centrar la comparación en la
relación de comportamiento. Si para una variable dependiente y tenemos definida una distancia
sobre
su conjunto de valores Vy, d:VyXVy→R+,
y tenemos una Actividad del Modelo y otra Actividad del Sistema Real
con los mismos valores de las variables de entrada, llamaremos grado de acoplamiento δy
de dicha variable y entre el
Modelo y el Sistema Real para dichas Actividades
al promedio entre la distancia entre los valores de y en dichas
actividades. El grado de ajuste
δ del comportamiento del Modelo al Sistema Real para dichas Actividades
será el promedio de los grados de acoplamiento para todas las
variables dependientes.Ejercicio
12: reconstruir la relación de comportamiento
correspondiente al problema de Caja Negra resuelto en el Ejercicio 11
mediante una Síntesis a partir de Sistemas suma, producto,
negación y retardo. Buscar la solución óptima.
NOTA: a su vez, los Sistemas suma, producto y negación podrían obtenerse por Síntesis a partir de un único Sistema booleano ¿Cuál sería éste?
Actividad 19. Para resolver un problema de Análisis de un conjunto de Sistemas interconectados (es decir, con variables comunes), comenzaremos
a) obteniendo su unión realista. Para ello
a1) juntaremos sus variables y
a2) representaremos su relación estructural de conexión, obtenida uniendo las relaciones estructurales de conexión de los distintos Sistemas, y comprobaremos que está bien determinada. Si no fuera así, es decir si aparecieran bucles en la relación estructural de conexión resultante, el problema de Análisis no tendría solución, y deberíamos en todo caso reformularlo modificando las conexiones entre los distintos Sistemas. Si la relación estructural de conexión resultante estuviera bien determinada, podríamos pasar a
a3) obtener la relación de comportamiento resultante de la intersección de las relaciones de comportamiento extendidas de los distintos Sistemas. Si éstas estuvieran expresadas a través de ecuaciones o inecuaciones, para ello bastaría con escribir el correspondiente sistema de ecuaciones o inecuaciones. Si estuvieran expresadas mediante tablas (asignando cada columna a una variable, y escribiendo en las distintas filas los valores compatibles de las distintas variables), comenzaríamos anotando en distintas filas todos los valores posibles de las variables de entrada. A continuación anotaríamos en las columnas correspondientes los valores compatibles de las variables de nivel 2 (replicando filas si es necesario), y seguiríamos así sucesivamente con las variables de los niveles siguientes hasta agotarlos.
b) A continuación realizaremos la reducción del Sistema obtenido eliminando las variables intermedias, es decir todas aquéllas que no sean ni de entrada ni de salida (ni eventualmente de estado). Si las relaciones de comportamiento venían dadas por ecuaciones o inecuaciones, dicha eliminación la realizaremos por procedimientos algebraicos si es posible. En caso contrario la realizaremos mediante tablas, simplemente suprimiendo en primer lugar las columnas de las variables intermedias, y en segundo lugar suprimiendo las filas repetidas. Finalmente, deberemos reexaminar las relaciones de dependencia, suprimiendo aquéllas que no afecten al valor de la correspondiente variable de salida (o de estado).
Ejercicio 13: obtener el Sistema resultante del Análisis del conjunto de Sistemas definidos por:
¿El Sistema resultante es un Sistema Dinámico? Clasificar
sus variables y obtener una Actividad del mismo (podéis escoger
libremente los valores de las variables de entrada).
Actividad 20. Para resolver un problema de Simulación podemos utilizar, según los casos, las técnicas correspondientes a los problemas anteriores. En general, la resolución constará de tres pasos:
a) Identificar el Sistema o Sistemas reales que queremos estudiar, seleccionando las variables relevantes y el conjunto de valores que consideraremos de cada una, teniendo en cuenta la precisión posible o deseada (Nivel de Resolución).
b) Construir un Sistema (Modelo) cuyas relaciones estructurales y de comportamiento repliquen las del Sistema o Sistemas reales que queremos estudiar. Para ello utilizaremos los conocimientos teóricos que tengamos sobre dichos Sistemas. Cuando dichos conocimientos sean insuficientes, podemos obtener por observación o experimentación una Actividad de un Sistema real, y comenzar resolviendo el correspondiente problema de Caja Negra. Para la construcción del Modelo buscaremos:
b1) identificar relaciones de causa-efecto entre las variables seleccionadas (relación estructural de conexión).
b2) asignar una representación funcional a dichas relaciones (relación de comportamiento).
c) Validar el Modelo, comprobando el ajuste del mismo a los Sistemas Reales en cuestión. Para ello:
c1) programaremos el modelo para una computadora o generaremos instrucciones para un grupo de expertos.
c2) efectuaremos si es necesario una calibración de determinados parámetros o variables auxiliares de entrada con un valor eventualmente constante pero inicialmente desconocido. Dicha calibración puede realizarse por tanteo mediante prueba y error o por regresión (determinando los valores que hacen mínima la desviación cuadrática entre el Modelo y los Sistemas Reales)
c3) realizaremos experimentos sobre el Modelo, comparando su Actividad con la Actividad de los Sistemas Reales que queremos simular e intentando determinar su grado de ajuste.
Si la validación no es satisfactoria pueden repetirse los pasos anteriores. Si se considera satisfactoria, presentaremos los resultados mediante tablas, gráficos, etc. y utilizaremos el Modelo para la toma de las decisiones pertinentes relativas a la acción sobre los Sistemas Reales.
Ejercicio 14: dividir la clase en 2 grupos; el primer grupo definirá un Sistema sencillo del cuál dará a conocer únicamente su Nivel de Resolución (sus variables relevantes y sus intervalos de valores a considerar); el segundo grupo intentará resolver un problema de Simulación sobre el mismo, para lo cuál podrá realizar preguntas al respecto; dichas preguntas pueden incluir información sobre el tipo de relaciones, o sobre el valor de determinadas variables, eventualmente intentando fijar el valor de otras; el primer grupo podrá escoger qué respuestas dar: si le intentan fijar un valor de una variable dependiente, deberá contestar que ello no es posible; si le preguntan el valor de una variable dependiente sin haber fijado el valor de las variables de las que depende, podrá contestar que falta información o fijar aleatoriamente el valor de éstas. Una vez obtenida la información que considere suficiente, el segundo grupo construirá un Modelo y lo validará obteniendo una Actividad del mismo y comparándola con la proporcionada por el primer grupo.
Actividad 21. En distintos pasos para la resolución de problemas en equipo suelen utilizarse diferentes técnicas. Algunas de las más usuales son:
a) Braimstorming o "tormenta de cerebros":
a1) el moderador expone los objetivos a conseguir y da la palabra a los miembros del grupo, que van exponiendo sus ideas brevemente sin cortapisas; en esta fase no se critica ni descarta ninguna idea, todas las cuáles son anotadas por el secretario;
a2) cuando se agota la primera fase al no surgir nuevas ideas, el moderador invita a los miembros del grupo a analizar sucesivamente las ideas aportadas dando razones a favor y en contra.
a3) el moderador recapitula el estado de la discusión señalando el grado de consenso o discrepancia existente.
b) Delphi, con un equipo director que envía un cuestionario por escrito a los expertos y tras recibir las respuestas las analiza, sintetiza y presenta por escrito de forma ordenada junto al siguiente cuestionario, y así sucesivamente hasta llegar a una aproximación que considere satisfactoria o constatar que hay discrepancias provisionalmente irreductibles.
Ejercicio 15: utilizar la técnica de Braimstorming en clase para responder a una pregunta abierta, por ejemplo qué factores influyen directa o indirectamente en el cambio climático; el objetivo será establecer una relación estructural de conexión.
Ejercicio 16: utilizar el método Delphi para responder a la misma pregunta; a tal efecto, el conjunto de la clase (o en su caso diferentes subgrupos) actuará como equipo director, elaborando un cuestionario y seleccionando un conjunto de expertos (pueden ser profesores, estudiantes de otros cursos, familiares, vecinos, etc.); los miembros de la clase se distribuirán a los expertos para llevarles el cuestionario y recoger las respuestas, que se analizarán en una sesión posterior dentro o fuera de clase, elaborando un nuevo cuestionario si se considera pertinente.
NOTA: a su vez, los Sistemas suma, producto y negación podrían obtenerse por Síntesis a partir de un único Sistema booleano ¿Cuál sería éste?
Actividad 19. Para resolver un problema de Análisis de un conjunto de Sistemas interconectados (es decir, con variables comunes), comenzaremos
a) obteniendo su unión realista. Para ello
a1) juntaremos sus variables y
a2) representaremos su relación estructural de conexión, obtenida uniendo las relaciones estructurales de conexión de los distintos Sistemas, y comprobaremos que está bien determinada. Si no fuera así, es decir si aparecieran bucles en la relación estructural de conexión resultante, el problema de Análisis no tendría solución, y deberíamos en todo caso reformularlo modificando las conexiones entre los distintos Sistemas. Si la relación estructural de conexión resultante estuviera bien determinada, podríamos pasar a
a3) obtener la relación de comportamiento resultante de la intersección de las relaciones de comportamiento extendidas de los distintos Sistemas. Si éstas estuvieran expresadas a través de ecuaciones o inecuaciones, para ello bastaría con escribir el correspondiente sistema de ecuaciones o inecuaciones. Si estuvieran expresadas mediante tablas (asignando cada columna a una variable, y escribiendo en las distintas filas los valores compatibles de las distintas variables), comenzaríamos anotando en distintas filas todos los valores posibles de las variables de entrada. A continuación anotaríamos en las columnas correspondientes los valores compatibles de las variables de nivel 2 (replicando filas si es necesario), y seguiríamos así sucesivamente con las variables de los niveles siguientes hasta agotarlos.
b) A continuación realizaremos la reducción del Sistema obtenido eliminando las variables intermedias, es decir todas aquéllas que no sean ni de entrada ni de salida (ni eventualmente de estado). Si las relaciones de comportamiento venían dadas por ecuaciones o inecuaciones, dicha eliminación la realizaremos por procedimientos algebraicos si es posible. En caso contrario la realizaremos mediante tablas, simplemente suprimiendo en primer lugar las columnas de las variables intermedias, y en segundo lugar suprimiendo las filas repetidas. Finalmente, deberemos reexaminar las relaciones de dependencia, suprimiendo aquéllas que no afecten al valor de la correspondiente variable de salida (o de estado).
Ejercicio 13: obtener el Sistema resultante del Análisis del conjunto de Sistemas definidos por:
|
|
|
Actividad 20. Para resolver un problema de Simulación podemos utilizar, según los casos, las técnicas correspondientes a los problemas anteriores. En general, la resolución constará de tres pasos:
a) Identificar el Sistema o Sistemas reales que queremos estudiar, seleccionando las variables relevantes y el conjunto de valores que consideraremos de cada una, teniendo en cuenta la precisión posible o deseada (Nivel de Resolución).
b) Construir un Sistema (Modelo) cuyas relaciones estructurales y de comportamiento repliquen las del Sistema o Sistemas reales que queremos estudiar. Para ello utilizaremos los conocimientos teóricos que tengamos sobre dichos Sistemas. Cuando dichos conocimientos sean insuficientes, podemos obtener por observación o experimentación una Actividad de un Sistema real, y comenzar resolviendo el correspondiente problema de Caja Negra. Para la construcción del Modelo buscaremos:
b1) identificar relaciones de causa-efecto entre las variables seleccionadas (relación estructural de conexión).
b2) asignar una representación funcional a dichas relaciones (relación de comportamiento).
c) Validar el Modelo, comprobando el ajuste del mismo a los Sistemas Reales en cuestión. Para ello:
c1) programaremos el modelo para una computadora o generaremos instrucciones para un grupo de expertos.
c2) efectuaremos si es necesario una calibración de determinados parámetros o variables auxiliares de entrada con un valor eventualmente constante pero inicialmente desconocido. Dicha calibración puede realizarse por tanteo mediante prueba y error o por regresión (determinando los valores que hacen mínima la desviación cuadrática entre el Modelo y los Sistemas Reales)
c3) realizaremos experimentos sobre el Modelo, comparando su Actividad con la Actividad de los Sistemas Reales que queremos simular e intentando determinar su grado de ajuste.
Si la validación no es satisfactoria pueden repetirse los pasos anteriores. Si se considera satisfactoria, presentaremos los resultados mediante tablas, gráficos, etc. y utilizaremos el Modelo para la toma de las decisiones pertinentes relativas a la acción sobre los Sistemas Reales.
Ejercicio 14: dividir la clase en 2 grupos; el primer grupo definirá un Sistema sencillo del cuál dará a conocer únicamente su Nivel de Resolución (sus variables relevantes y sus intervalos de valores a considerar); el segundo grupo intentará resolver un problema de Simulación sobre el mismo, para lo cuál podrá realizar preguntas al respecto; dichas preguntas pueden incluir información sobre el tipo de relaciones, o sobre el valor de determinadas variables, eventualmente intentando fijar el valor de otras; el primer grupo podrá escoger qué respuestas dar: si le intentan fijar un valor de una variable dependiente, deberá contestar que ello no es posible; si le preguntan el valor de una variable dependiente sin haber fijado el valor de las variables de las que depende, podrá contestar que falta información o fijar aleatoriamente el valor de éstas. Una vez obtenida la información que considere suficiente, el segundo grupo construirá un Modelo y lo validará obteniendo una Actividad del mismo y comparándola con la proporcionada por el primer grupo.
Actividad 21. En distintos pasos para la resolución de problemas en equipo suelen utilizarse diferentes técnicas. Algunas de las más usuales son:
a) Braimstorming o "tormenta de cerebros":
a1) el moderador expone los objetivos a conseguir y da la palabra a los miembros del grupo, que van exponiendo sus ideas brevemente sin cortapisas; en esta fase no se critica ni descarta ninguna idea, todas las cuáles son anotadas por el secretario;
a2) cuando se agota la primera fase al no surgir nuevas ideas, el moderador invita a los miembros del grupo a analizar sucesivamente las ideas aportadas dando razones a favor y en contra.
a3) el moderador recapitula el estado de la discusión señalando el grado de consenso o discrepancia existente.
b) Delphi, con un equipo director que envía un cuestionario por escrito a los expertos y tras recibir las respuestas las analiza, sintetiza y presenta por escrito de forma ordenada junto al siguiente cuestionario, y así sucesivamente hasta llegar a una aproximación que considere satisfactoria o constatar que hay discrepancias provisionalmente irreductibles.
Ejercicio 15: utilizar la técnica de Braimstorming en clase para responder a una pregunta abierta, por ejemplo qué factores influyen directa o indirectamente en el cambio climático; el objetivo será establecer una relación estructural de conexión.
Ejercicio 16: utilizar el método Delphi para responder a la misma pregunta; a tal efecto, el conjunto de la clase (o en su caso diferentes subgrupos) actuará como equipo director, elaborando un cuestionario y seleccionando un conjunto de expertos (pueden ser profesores, estudiantes de otros cursos, familiares, vecinos, etc.); los miembros de la clase se distribuirán a los expertos para llevarles el cuestionario y recoger las respuestas, que se analizarán en una sesión posterior dentro o fuera de clase, elaborando un nuevo cuestionario si se considera pertinente.
Si tenemos definida congruentemente una medida sobre el conjunto de valores Vy de la variable dependiente y, m:Vy→R+, llamaremos grado de acoplamiento relativo ρy de dicha variable y entre el Modelo y el Sistema Real para unas Actividades de los mismos al cociente entre su grado de acoplamiento y el promedio de la medida del valor de y en el Sistema Real en la correspondiente Actividad del mismo, ρy=δy/μ(m(y)). El grado de ajuste relativo ρ del comportamiento del Modelo al Sistema Real para dichas Actividades será el promedio de los grados de acoplamiento relativo para todas las variables dependientes.
Ejercicio 17: calcular el grado de ajuste y el grado de ajuste relativo del Modelo obtenido en el Ejercicio 14 (u otro).
Objetivos:
- Aprender a calcular medidas de centralidad y dispersión de una distribución estadística.
- Aprender a calcular probabilidades absolutas y condicionales de un determinado suceso.
- Aprender a realizar estimaciones sobre una población a partir de una muestra de la misma.
- Aprender a obtener la regresión lineal de dos variables aleatorias.
- Aprender a trabajar con posibilidades absolutas y condicionales.
Actividad 23. Una variable aleatoria (X) en un conjunto-población es cualquier variable que puede tener distintos valores (x) para los distintos elementos-individuos de la población. La distribución estadística de dichos valores no tiene en cuenta los individuos concretos para los que dicha variable tiene cada valor, sino cuántos la tienen, a lo que llamamos frecuencia de dicho valor en la población. Llamaremos parámetro poblacional a cualquier cantidad que sólo dependa de las frecuencias. Para caracterizar una distribución estadística, nos interesará conocer su centralidad, dada por un valor alrededor del cuál se agrupan los valores de la variable aleatoria, y su dispersión, para expresar el alejamiento de dichos valores entre sí.
Como medidas de centralidad podemos tomar:
La moda: aquel valor que tenga la máxima frecuencia en la población.
La mediana: suponiendo que el conjunto de valores de la variable aleatoria esté ordenado, será un valor que tenga tantos individuos con un valor inferior como con un valor superior.
La media μ(X): suponiendo que los valores de la variable aleatoria sean cantidades sumables, y que el tamaño (número de individuos) de la población sea finito, viene dada por la suma de los valores para todos los individuos de la població dividida por su tamaño.
Como medidas de dispersión podemos tomar:
Los cuartiles primero y tercero: suponiendo que el conjunto de valores de la variable aleatoria esté ordenado, los cuartiles serán tres valores que dividan al conjunto de valores en cuatro subconjuntos de valores que correspondan al mismo número de individuos; obsérvese que el segundo cuartil coincidirá con la mediana. Si tenemos definida una distancia en el conjunto de valores, podemos medir la dispersión como la distancia entre el primer y el tercer cuartil.
La amplitud: suponiendo que además tengamos definida una distancia en el conjunto de valores, será la distancia entre los valores mínimo y máximo en la población.
La desviación media: suponiendo que los valores de la variable aleatoria sean cantidades sumables, y que el tamaño de la población sea finito, será la media del valor absoluto de las diferencias entre su valor para cada individuo y su valor medio
La varianza σ2(X): suponiendo que los valores de la variable aleatoria sean cantidades sumables, y que el tamaño de la población sea finito, será la media del cuadrado de las diferencias entre su valor para cada individuo y su valor medio [σ2(X)=μ((X-μ(X))2)]. La varianza puede calcularse también como la media de los cuadrados menos el cuadrado de la media [σ2(X)=μ(X2)-μ(X)2] . Para calcularla de esta forma, y en el caso de que la media sea mucho mayor que la amplitud, conviene restar a todos los valores una cantidad fija próxima a su valor mínimo, operación que no modificará la dispersión.
La desviación típica σ(X): es la raiz cuadrada de la varianza.
Llamaremos normalización de una variable al resultado de restarle su media y dividir la diferencia por su desviación típica, N(X)=(X-μ(X))/σ(X) ; la media de la variable normalizada valdrá cero [μ(N(X))=0] y su desviación típica valdrá uno [σ(N(X))=1].
Ejercicio 18: definir una variable aleatoria (por ejemplo, el número de calzado) en la población definida por los alumnos de la asignatura, y obtener todos los parámetros poblacionales definidos en esta actividad. Estudiar cómo simplificar el cálculo de algunos de ellos utilizando las frecuencias.
Actividad 24. Llamaremos probabilidad de un subconjunto de valores de una variable aleatoria al cociente entre el número de individuos que tienen alguno de los valores del subconjunto y el tamaño de la población. Si el conjunto de valores es finito, podremos calcular la probabilidad de cada valor como su frecuencia dividida por el tamaño de la población, y la probabilidad de un subconjunto de valores como la suma de las probabilidades de cada uno de ellos. En tal caso, la suma de las probabilidades de todos los valores será igual a 1: llamaremos distribución probabilística a cualquier aplicación que asigne un número real no negativo a cada valor de un conjunto de valores tal que su suma valga 1. Si el conjunto de valores no es finito, pero tenemos definida una medida sobre el mismo, llamaremos distribución de densidad probabilística a cualquier aplicación que asigne un número real no negativo a cada valor tal que su integral valga 1: la probabilidad de un subconjunto de valores vendrá dada por la integral de dicha aplicación sobre el mismo.
Ejercicio 19: estudiar cómo obtener la media de una variable aleatoria conociendo su distribución probabilística. Aplicarlo al caso del Ejercicio 18. ¿Cómo podríamos definir la media de una distribución de densidad probabilística?
Actividad 25: Si trabajamos con dos variables aleatorias X,Y combinadas, podemos obtener del mismo modo la probabilidad (absoluta) P(x,y) de que dichas variables tengan simultáneamente unos valores determinados contando el número de individuos en que ello se produzca y dividiéndolo por el tamaño de la población. Pero en determinadas ocasiones nos interesará conocer la probabilidad condicional, P(y|x), definida como la probabilidad de un valor (y) de una variable (Y) restringida a la subpoblación definida por un determinado valor (x) de otra variable (X). Para ello podemos contar el número de individuos que tienen el par de valores (x.y) y dividirlo por el número de individuos que tienen el valor (x) de la segunda variable, que será el tamaño de la subpoblación. Pero podemos también calcular la probabilidad condicional utilizando el Teorema de Bayes, que nos dice que P(y|x)=P(x,y)/P(x) . Si las dos variables aleatorias son independientes, la probabilidad condicional coincidirá con la probabilidad absoluta del valor de la primera variable, P(y|x)=P(y), y se cumplirá que P(x,y)=P(x)P(y) .
Ejercicio 20: combinar la variable aleatoria estudiada en el Ejercicio 18 con otra variable definida en el conjunto de alumnos de la asignatura (por ejemplo, el sexo o la edad). Obtener las probabilidades condicionadas de la primera variable respecto de la segunda. ¿Son independientes? A partir de la probabilidades ya calculadas, y fijando el valor de la primera variable, obtener la probabilidad condicional de la segunda variable respecto de dicho valor.
Ejercicio 21: en una ciudad multiétnica se comete un delito. Un testigo afirma que dicho delito ha sido cometido por una persona "de color". Pero reproduciendo la situación en las mismas condiciones de iluminación se encuentra que el testigo acierta el "color" en un 70% de los casos, tanto si es realmente "de color" como "blanca". Sabiendo que en la ciudad hay un 10% de personas "de color", calcular cuál es la probabilidad de que el delito haya sido cometido realmente por una persona "de color".
Actividad 26. Llamamos muestra (sin reemplazamiento) de una población a cualquier subconjunto de la misma. Una muestra con reemplazamiento se obtendrá extrayendo sucesivamente individuos de la población sin suprimirlos de la misma. Llamamos estadístico a cualquier parámetro poblacional restringido a una muestra, como la media muestral ¯X o la desviación típica muestral s(X) [naturalmente, para los estadisticos se cumplen la mismas relaciones que para los parámetros poblacionales correspondientes, por ejemplo s2(X)=¯(X2)-(¯X)2 ]. Y llamamos distribución muestral a la distribución de un estadístico en el conjunto de todas las muestras de la población de un cierto tamaño n. Los parámetros poblacionales de la distribución muestral, como la media de las medias μ(¯X), la varianza de las medias σ2(¯X) o la media de las varianzas μ(s2(X)), son importantes para realizar estimaciones a partir del estadístico de una muestra sobre el correspondiente parámetro poblacional. A tal efecto, hay que tener en cuenta las siguientes relaciones:
μ(¯X)=μ(X)
σ2(¯X)=σ2(X)/n si las muestras son con reemplazamiento o la población es infinita (aproximadamente, si es muy grande).
μ(s2(X))=σ2(X)·(n-1)/n
Diremos que un estadístico es insesgado cuando la media de su distribución muestral es igual al correspondiente parámetro poblacional. Para estimar un parámetro poblacional a partir de un estadístico, éste debe ser insesgado.
Ejercicio 22: ¿la media y la varianza muestrales son estadísticos insesgados? En caso de que alguna de ellas no lo sea, ¿cómo podríamos obtener un estadístico corregido que sí fuera insesgado? Tomando el conjunto de alumnos de la asignatura como una muestra del conjunto de alumnos de la licenciatura, realizar una estimación sobre este conjunto de la media y de la varianza de la variable aleatoria del Ejercicio 18. Estimar también la varianza de la distribución muestral de las medias.
Actividad 27. Diremos que [S1,S2] es un intervalo de confianza del 100α% para un parámetro poblacional Ω si la probabilidad de que Ω se encuentre en dicho intervalo es igual a α. Para poder obtener intervalos de confianza necesitaremos conocer la distribución muestral de un estadístico insesgado S de dicho parámetro poblacional.
Definimos la distribución normal como la distribución de densidad probabilística dada por la fórmula
p(x) = exp(-(x-μ)2/(2σ2))/(σ(2π)1/2)
Si las muestras son pequeñas pero la distribución de la
variable aleatoria X en la población corresponde a una
distribución normal, entonces la distribución muestral de
las medias de la correspondiente variable aleatoria normalizada,Se demuestra que si la población
es infinita y las muestras son grandes, la distribución muestral
de las medias se aproxima a la distribución normal. Trabajando
con una variable aleatoria normalizada N(X)=(X-μ(X))/σ(X), la
distribución muestral de sus medias se aproximará a la
distribución normal tipificada, que es la que tiene una media
μ=0 y una desviación típica σ=1,
p(x) = exp(-x2/2)/(2π)1/2
t = (¯X-μ(¯X))/σ(¯X) ,
se ajusta a una distribución t de Student, definida porpν(t) = pν(0)·(1+t2/ν)-(ν+1)/2
con ν=n-1 grados de libertad, siendo n
el tamaño de las muestras y escogiendo pν(0)
de modo que la integral entre menos infinito y más infinito de pν(t)
valga la unidad, de modo que sea una distribución de densidad
probabilística. En la práctica, puede utilizarse como
aproximación la distribución t de Student si el
tamaño de la población es mucho mayor que el de la
muestra. Se demuestra que si ν tiende a infinito la distribución
t de Student tiende
a la distribución normal tipificada. Llamaremos coeficiente de confianza tα(ν)
al valor de t tal que la probabilidad de encontrarse entre -tα(ν)
y tα(ν) dada por una distribución t de Student con ν grados de
libertad sea igual a α.
Ejercicio 23: para obtener un intervalo de confianza del 80% para la media μ(X) de la variable aleatoria del Ejercicio 18 en el conjunto de alumnos de la licenciatura a partir de la media ¯X y de la desviación típica s(X) en el conjunto de alumnos de la asignatura, comenzaremos estimando la desviación típica σ(X) de la población mediante la desviación típica corregida ^s(X) para ser insesgada. A partir del valor estimado de σ(X) calcularemos la desviación típica σ(¯X) de la distribución muestral mediante la fórmula de la Actividad 26. De la tabla de la distribución t de Student obtendremos el coeficiente de confianza t0'80(ν) (deberemos fijarnos en la figura que encabeza la tabla para determinar cuál es la columna que corresponde a dicho coeficiente de confianza). Y finalmente utilizaremos la expresión de la media t de la correspondiente variable aleatoria normalizada y la condición -t0'80(ν) < t < t0'80(ν) para obtener el intervalo de confianza del 80% para μ(X).
Ejercicio 23: para obtener un intervalo de confianza del 80% para la media μ(X) de la variable aleatoria del Ejercicio 18 en el conjunto de alumnos de la licenciatura a partir de la media ¯X y de la desviación típica s(X) en el conjunto de alumnos de la asignatura, comenzaremos estimando la desviación típica σ(X) de la población mediante la desviación típica corregida ^s(X) para ser insesgada. A partir del valor estimado de σ(X) calcularemos la desviación típica σ(¯X) de la distribución muestral mediante la fórmula de la Actividad 26. De la tabla de la distribución t de Student obtendremos el coeficiente de confianza t0'80(ν) (deberemos fijarnos en la figura que encabeza la tabla para determinar cuál es la columna que corresponde a dicho coeficiente de confianza). Y finalmente utilizaremos la expresión de la media t de la correspondiente variable aleatoria normalizada y la condición -t0'80(ν) < t < t0'80(ν) para obtener el intervalo de confianza del 80% para μ(X).
Actividad 28. Si la distribución de una variable aleatoria X en una población infinita se ajusta a una distribución normal, la distribución muestral del estadístico
χ2 =
n·s2(X)/σ2(X)
se ajusta a una distribución Ji-cuadrado, definida por
Actividad 30. Si tenemos dos variables aleatorias numéricas X e Y, llamaremos covarianza de las mismas a
pν(χ2)
= Kν·(χ2)(ν-2)/2·exp(-χ2/2)
con ν=n-1 grados de libertad, siendo n
el tamaño de las muestras y escogiendo Kν
de modo que la integral entre menos infinito y más infinito de pν(χ2)
valga la unidad, de modo que sea una distribución de densidad
probabilística. Llamaremos coeficiente
crítico χ2p(ν) al
valor de χ2 tal que la probabilidad de
encontrar un valor mayor o igual en una distribución Ji-cuadrado
con ν grados de libertad sea igual a p.
Ejercicio 24: para obtener un intervalo de confianza del 80% para la varianza σ2(X) de la variable aleatoria del Ejercicio 18 en el conjunto de alumnos de la licenciatura a partir de la varianza s2(X) en el conjunto de alumnos de la asignatura buscaremos en la tabla de la distribución Ji-cuadrado dos coeficientes críticos χ2p(ν) y χ21-p(ν) tales que la probabilidad de que el estadístico χ2 se encuentre entre ellos sea de 0'80, y utilizaremos la expresión de dicho estadístico para obtener el intervalo de confianza del 80% para σ2(X). Obtener el correspondiente intervalo de confianza del 80% para la desviación típica σ(X) de la población y comprobar que la desviación típica corregida ^s(X) de la muestra pertenece a dicho intervalo.
Actividad 29. Si tenemos una variable aleatoria con k valores i=1,2..k, una hipótesis que les asigna probabilidades p(i), y una muestra de tamaño n, llamaremos frecuencia esperada del valor i en dicha muestra a ei=n·p(i), y frecuencia observada oi a su frecuencia en la muestra. Se demuestra que si todas las frecuencias esperadas son igual o mayor que 5, entonces la distribución del estadístico χ2 obtenido sumando (oi-ei)2/ei para todos los valores de la variable aleatoria se aproxima a la distribución Ji-cuadrado con grados de libertad ν=k-1 (prueba Ji-cuadrado). Si dicho estadístico es superior a χ2β(ν), diremos que la hipótesis probabilística es rechazada por la muestra con un nivel de significación β. Si dicho estadístico es inferior a χ21-β(ν), diremos hay concordancia entre la hipótesis y la muestra con un nivel de significación β. Si el estadístico se encontrara entre dichos dos valores, diremos que la muestra no es definitoria para la hipótesis con ese nivel de significación.
Ejercicio 25: arrojar un dado 30 veces, anotar el número de veces que se obtiene cada cara y realizar realizar estimaciones sobre hipótesis probabilísticas en relación al dado.
Ejercicio 24: para obtener un intervalo de confianza del 80% para la varianza σ2(X) de la variable aleatoria del Ejercicio 18 en el conjunto de alumnos de la licenciatura a partir de la varianza s2(X) en el conjunto de alumnos de la asignatura buscaremos en la tabla de la distribución Ji-cuadrado dos coeficientes críticos χ2p(ν) y χ21-p(ν) tales que la probabilidad de que el estadístico χ2 se encuentre entre ellos sea de 0'80, y utilizaremos la expresión de dicho estadístico para obtener el intervalo de confianza del 80% para σ2(X). Obtener el correspondiente intervalo de confianza del 80% para la desviación típica σ(X) de la población y comprobar que la desviación típica corregida ^s(X) de la muestra pertenece a dicho intervalo.
Actividad 29. Si tenemos una variable aleatoria con k valores i=1,2..k, una hipótesis que les asigna probabilidades p(i), y una muestra de tamaño n, llamaremos frecuencia esperada del valor i en dicha muestra a ei=n·p(i), y frecuencia observada oi a su frecuencia en la muestra. Se demuestra que si todas las frecuencias esperadas son igual o mayor que 5, entonces la distribución del estadístico χ2 obtenido sumando (oi-ei)2/ei para todos los valores de la variable aleatoria se aproxima a la distribución Ji-cuadrado con grados de libertad ν=k-1 (prueba Ji-cuadrado). Si dicho estadístico es superior a χ2β(ν), diremos que la hipótesis probabilística es rechazada por la muestra con un nivel de significación β. Si dicho estadístico es inferior a χ21-β(ν), diremos hay concordancia entre la hipótesis y la muestra con un nivel de significación β. Si el estadístico se encontrara entre dichos dos valores, diremos que la muestra no es definitoria para la hipótesis con ese nivel de significación.
Ejercicio 25: arrojar un dado 30 veces, anotar el número de veces que se obtiene cada cara y realizar realizar estimaciones sobre hipótesis probabilísticas en relación al dado.
Actividad 30. Si tenemos dos variables aleatorias numéricas X e Y, llamaremos covarianza de las mismas a
cXY=μ(X·Y)-μ(X)·μ(Y)
y diremos que y=a+bx es la recta de
regresión de Y sobre X si la suma de los cuadrados de las
diferencias entre a+bX e Y es la mínima posible. Se demuestra
que la recta de regresión pasa por el punto (μ(X), μ(Y)), y que
si la varianza de X es mayor que cero, entonces dicha recta se obtiene
tomandob=cXY/σ2(X),
y=μ(Y)+b·(x-μ(X)).
Si la varianza de Y es también
mayor que cero, definimos el coeficiente
de correlación entre X e Y por
ρXY = cXY/(σ(X)σ(Y))
Se demuestra fácilmente que si X
e Y son independientes entonces cXY=0, y por
tanto ρXY=0 (la recíproca no es
cierta).
Teniendo en cuenta que μ( ) es lineal y que σ(a+bX)=|b|σ(X) se demuestra también fácilmente que si los puntos (X,Y) están alineados sobre la recta de regresión, es decir Y=a+bX, entonces ρXY=±1 (según cuál sea el signo de b).
El coeficiente de correlación mide el grado de ajuste de la recta de regresión: si vale 0 diremos que no hay correlación lineal (aunque puede haber correlación no lineal), y si vale ±1 diremos que la correlación lineal es perfecta. Si ρXY>0 diremos que la correlación lineal es positiva, y si ρXY<0 diremos que es negativa.
Ejercicio 26: comprobar que si X e Y son independientes entonces cXY=0 y que si Y=a+bX entonces ρXY=±1
Ejercicio 28: obtener la recta
de regresión y estudiar la correlación lineal entre dos
variables aleatorias (por ejemplo, la edad y el número de
calzado) en la
población definida por los alumnos de la asignatura.
Actividad 31. Puede darse el caso de que no conozcamos las frecuencias relativas (es decir, las probabilidades) de los distintos valores de una variable aleatoria X, y debamos limitarnos a estimar su posibilidad entre 0 y 1. Dado que la variable deberá tener algún valor, deberá haber algún valor x con posibilidad π(x)=1. Así, llamaremos distribución posibilística a cualquier aplicación que asigne un número real no negativo a cada valor de un conjunto E de valores, de modo que su máximo sea 1. Para todo subconjunto A de valores, su posibilidad π(A) vendrá dada por el máximo de dicha aplicación sobre el mismo, y definiremos su necesidad como ν(A)=1-π(E-A); obtendremos la necesidad de un valor x mediante ν(x)=1-π(E-{x}).
Si trabajamos con dos variables aleatorias X,Y combinadas, podemos estimar también la posibilidad (absoluta) π(x,y) de que dichas variables tengan simultáneamente unos valores determinados. En tal caso, π(x) será la posibilidad del conjunto {(x,Y)}, es decir, el máximo para todo y de π(x,y). A su vez, π(y) será la posibilidad del conjunto {(X,y)}, es decir, el máximo para todo x de π(x,y).Y definiremos la posibilidad condicional π(y|x) mediante
π(y|x) = π(x,y) si π(x)>π(x,y)
π(y|x) = 1 si π(x)=π(x,y)
A partir de la posibilidad condicional π(y|x) puede obtenerse la posibilidad absoluta π(x,y), que será el mínimo de π(x) y π(y|x).
Ejercicio 29: dividir la clase en 2 grupos; el primer grupo definirá dos variables aleatorias X, Y, estimará los valores de las posibilidades absolutas π(x,y) y calculará y hará públicas los valores de la posibilidad condicional π(y|x) y de la posibilidad π(x); a partir de ellos, el segundo grupo calculará los valores de la posibilidad condicional π(x|y) y de la necesidad ν(x).
Teniendo en cuenta que μ( ) es lineal y que σ(a+bX)=|b|σ(X) se demuestra también fácilmente que si los puntos (X,Y) están alineados sobre la recta de regresión, es decir Y=a+bX, entonces ρXY=±1 (según cuál sea el signo de b).
El coeficiente de correlación mide el grado de ajuste de la recta de regresión: si vale 0 diremos que no hay correlación lineal (aunque puede haber correlación no lineal), y si vale ±1 diremos que la correlación lineal es perfecta. Si ρXY>0 diremos que la correlación lineal es positiva, y si ρXY<0 diremos que es negativa.
Ejercicio 26: comprobar que si X e Y son independientes entonces cXY=0 y que si Y=a+bX entonces ρXY=±1
| Ejercicio
27: estudiar la correlación lineal en el caso |
|
¿X e Y son
independientes? |
Actividad 31. Puede darse el caso de que no conozcamos las frecuencias relativas (es decir, las probabilidades) de los distintos valores de una variable aleatoria X, y debamos limitarnos a estimar su posibilidad entre 0 y 1. Dado que la variable deberá tener algún valor, deberá haber algún valor x con posibilidad π(x)=1. Así, llamaremos distribución posibilística a cualquier aplicación que asigne un número real no negativo a cada valor de un conjunto E de valores, de modo que su máximo sea 1. Para todo subconjunto A de valores, su posibilidad π(A) vendrá dada por el máximo de dicha aplicación sobre el mismo, y definiremos su necesidad como ν(A)=1-π(E-A); obtendremos la necesidad de un valor x mediante ν(x)=1-π(E-{x}).
Si trabajamos con dos variables aleatorias X,Y combinadas, podemos estimar también la posibilidad (absoluta) π(x,y) de que dichas variables tengan simultáneamente unos valores determinados. En tal caso, π(x) será la posibilidad del conjunto {(x,Y)}, es decir, el máximo para todo y de π(x,y). A su vez, π(y) será la posibilidad del conjunto {(X,y)}, es decir, el máximo para todo x de π(x,y).Y definiremos la posibilidad condicional π(y|x) mediante
π(y|x) = π(x,y) si π(x)>π(x,y)
π(y|x) = 1 si π(x)=π(x,y)
A partir de la posibilidad condicional π(y|x) puede obtenerse la posibilidad absoluta π(x,y), que será el mínimo de π(x) y π(y|x).
Ejercicio 29: dividir la clase en 2 grupos; el primer grupo definirá dos variables aleatorias X, Y, estimará los valores de las posibilidades absolutas π(x,y) y calculará y hará públicas los valores de la posibilidad condicional π(y|x) y de la posibilidad π(x); a partir de ellos, el segundo grupo calculará los valores de la posibilidad condicional π(x|y) y de la necesidad ν(x).
Objetivos:
- Aprender a identificar y distinguir el objetivo, las condiciones externas, la acción de control y la información en un Sistema Cibernético.
- Desarrollar procedimientos para escoger la acción adecuada para la consecución de un objetivo.
- Construir modelos sencillos de adaptación para la
consecución de un objetivo.
Actividad 32. Norbert Wiener (1948) definió la Cibernética como la ciencia de la comunicación y el control en el hombre, el animal y la máquina. Aquí "comunicación" hace referencia al intercambio de información entre un Sistema y su entorno, y "control" hace referencia a la realización de las acciones necesarias para obtener los resultados deseados: llamaremos Sistema Cibernético (y también "Sistema con objetivo" o "Sistema controlador") a un Sistema capaz de modificar sus respuestas a partir de la información recibida a fin de alcanzar un objetivo:

El "lazo de retorno", "feed-back" o
retroalimentación de la información, tanto sobre sobre el
grado de consecución o la distancia al objetivo como sobre las
condiciones externas en que ello se produce, es esencial para que un
Sistema Cibernético pueda conseguir su objetivo.
Señalemos que los Sistemas Cibernéticos pueden acoplarse,
de modo que el Objetivo de un Sistema Cibernético puede estar
determinado por la acción de control de otro Sistema
Cibernético.
Ejercicio 30: poner ejemplos de Sistemas Cibernéticos, identificando el objetivo, la información y la acción de control.
Ejercicio 31: dividir la clase en dos grupos; el primero, que actuará como Sistema Cibernético, definirá su objetivo; el segundo, que actuará como Sistema Controlado, definirá públicamente un conjunto de acciones a realizar o evitar para su consecución, y establecerá secretamente una relación de comportamiento entre dichas acciones, determinadas condiciones externas y el objetivo. A partir de ello, el segundo grupo anunciará las condiciones externas, el primer grupo anunciará sus acciones, y el segundo informará del consiguiente grado de consecución del objetivo. El proceso se repetirá hasta que el primer grupo consiga una suficiente estabilidad de su objetivo.
Actividad 33. En un Sistema Cibernético con control determinista simple, con una variable objetivo g, unas condiciones externas x y una variable de control u, tendremos una relación funcional g=f(x,u). En tal caso, se tratará de escoger, para cada valor de x, una acción u que permita, si es posible, la consecución del objetivo. Para ello habrá que definir qué valores de g son aceptables o una gradación de su aceptabilidad. Si el valor de g expresa simplemente un grado de consecución del objetivo, habrá simplemente que escoger, para cada valor de x, aquella acción u que conduzca al máximo valor posible de g. Si sólo algún o algunos valores de g son aceptables, para determinados valores de x puede que no exista ninguna acción u que permita la consecución del objetivo. En general, cuando mayor sea la variabilidad de las condiciones externas hará falta un número mayor de posible acciones de control para poder controlar la consecución del objetivo, cosa que Ashby (1958) expresó en lo que llamó la Ley de la Variedad Requerida.
Actividad 34. En el caso de un Sistema Cibernético Dinámico Adaptativo, éste modificaría el valor de una variable de estado tendiendo a aproximarlo a un valor "ideal" (objetivo). Así, diremos que una variable y tiende linealmente a una variable objetivo yI cuando se cumple y(t+1) = y(t) + (yI(t)-y(t))/Ty, donde Ty es el tiempo de retardo de la adaptación de dicha variable. Naturalmente, si el tiempo de retardo fuera la unidad se cumpliría y(t+1)=yI(t). En general, el Sistema debería recibir información sobre la diferencia entre el valor actual de la variable y su valor "ideal", z=yI-y, siendo la acción de control Δy=z/Ty.
Ejercicio 33: dividir la clase en dos grupos, cada uno de los cuáles tendrá un Sistema Cibernético Dinámico Adaptativo con una variable (x e y, respectivamente) que tenderá linealmente a una variable objetivo, y podrá escoger y variar libremente su tiempo de retardo. Suponiendo que xI=3-y, yI=x+1, partir de x=0, y=0 e iterar sucesivamente hasta que las diferencias entre ambas variables y sus respectivos valores "ideales" sean menores que una cantidad previamente acordada.
Actividad 35. Diremos que una variable dinámica aleatoria y con valores {y1,y2,...yM} es reforzada linealmente por una variable objetivo g con valores en el intervalo [0,1] si y sólo si existe una variable dinámica aleatoria f (a la que llamamos acumuladora de memoria) tal que
P(yk) = fk/B con B=∑j=1M fj (memoria acumulada) &
si y(t) = yk , entonces fk(t+1) = fk(t) + (2g(t)-1) [o 0 si fuera negativo] & en caso contrario fk(t+1) = fk(t)
para todo k=1,2...M
Es fácil comprobar que si g(t)=1 (objetivo plenamente satisfecho) con un determinado valor de y, entonces el correspondiente valor de la variable f acumuladora de memoria se incrementa en 1, y su probabilidad aumenta (sufre refuerzo positivo), mientras que si g(t)=0 (objetivo totalmente insatisfecho) con un determinado valor de y, entonces el correspondiente valor de la variable f acumuladora de memoria se decrementa en 1, y su probabilidad disminuye (sufre refuerzo negativo).
Ejercicio 30: poner ejemplos de Sistemas Cibernéticos, identificando el objetivo, la información y la acción de control.
Ejercicio 31: dividir la clase en dos grupos; el primero, que actuará como Sistema Cibernético, definirá su objetivo; el segundo, que actuará como Sistema Controlado, definirá públicamente un conjunto de acciones a realizar o evitar para su consecución, y establecerá secretamente una relación de comportamiento entre dichas acciones, determinadas condiciones externas y el objetivo. A partir de ello, el segundo grupo anunciará las condiciones externas, el primer grupo anunciará sus acciones, y el segundo informará del consiguiente grado de consecución del objetivo. El proceso se repetirá hasta que el primer grupo consiga una suficiente estabilidad de su objetivo.
Actividad 33. En un Sistema Cibernético con control determinista simple, con una variable objetivo g, unas condiciones externas x y una variable de control u, tendremos una relación funcional g=f(x,u). En tal caso, se tratará de escoger, para cada valor de x, una acción u que permita, si es posible, la consecución del objetivo. Para ello habrá que definir qué valores de g son aceptables o una gradación de su aceptabilidad. Si el valor de g expresa simplemente un grado de consecución del objetivo, habrá simplemente que escoger, para cada valor de x, aquella acción u que conduzca al máximo valor posible de g. Si sólo algún o algunos valores de g son aceptables, para determinados valores de x puede que no exista ninguna acción u que permita la consecución del objetivo. En general, cuando mayor sea la variabilidad de las condiciones externas hará falta un número mayor de posible acciones de control para poder controlar la consecución del objetivo, cosa que Ashby (1958) expresó en lo que llamó la Ley de la Variedad Requerida.
| Ejercicio
32: supongamos que tenemos un sistema controlado con una
variable objetivo g, unas
condiciones externas x y unas
acciones de control u, cuyo
comportamiento se expresa por la siguiente tabla de doble entrada: Los miembros de la clase, individualmente o agrupados, deberán definir su objetivo en relación al valor de la variable g, y de acuerdo con ello establecer el comportamiento de su Sistema Cibernético, u=u(x). El profesor irá dando valores de las condiciones externas x, y cada cuál dirá su correspondiente acción de control. A partir de ello, se intentará averiguar cuál era el objetivo de cada cuál. ¿Qué relación podría establecerse entre el número de posibles condiciones externas, el número de posibles acciones de control y la capacidad de restringir los valores de la variable objetivo? (obsérvese que, en el caso estudiado, para cada acción de control a distintas condiciones externas les corresponden distintos valores de la variable objetivo). |
|
|||||||||||||||||||||||||||||||||
Actividad 34. En el caso de un Sistema Cibernético Dinámico Adaptativo, éste modificaría el valor de una variable de estado tendiendo a aproximarlo a un valor "ideal" (objetivo). Así, diremos que una variable y tiende linealmente a una variable objetivo yI cuando se cumple y(t+1) = y(t) + (yI(t)-y(t))/Ty, donde Ty es el tiempo de retardo de la adaptación de dicha variable. Naturalmente, si el tiempo de retardo fuera la unidad se cumpliría y(t+1)=yI(t). En general, el Sistema debería recibir información sobre la diferencia entre el valor actual de la variable y su valor "ideal", z=yI-y, siendo la acción de control Δy=z/Ty.
Ejercicio 33: dividir la clase en dos grupos, cada uno de los cuáles tendrá un Sistema Cibernético Dinámico Adaptativo con una variable (x e y, respectivamente) que tenderá linealmente a una variable objetivo, y podrá escoger y variar libremente su tiempo de retardo. Suponiendo que xI=3-y, yI=x+1, partir de x=0, y=0 e iterar sucesivamente hasta que las diferencias entre ambas variables y sus respectivos valores "ideales" sean menores que una cantidad previamente acordada.
Actividad 35. Diremos que una variable dinámica aleatoria y con valores {y1,y2,...yM} es reforzada linealmente por una variable objetivo g con valores en el intervalo [0,1] si y sólo si existe una variable dinámica aleatoria f (a la que llamamos acumuladora de memoria) tal que
P(yk) = fk/B con B=∑j=1M fj (memoria acumulada) &
si y(t) = yk , entonces fk(t+1) = fk(t) + (2g(t)-1) [o 0 si fuera negativo] & en caso contrario fk(t+1) = fk(t)
para todo k=1,2...M
Es fácil comprobar que si g(t)=1 (objetivo plenamente satisfecho) con un determinado valor de y, entonces el correspondiente valor de la variable f acumuladora de memoria se incrementa en 1, y su probabilidad aumenta (sufre refuerzo positivo), mientras que si g(t)=0 (objetivo totalmente insatisfecho) con un determinado valor de y, entonces el correspondiente valor de la variable f acumuladora de memoria se decrementa en 1, y su probabilidad disminuye (sufre refuerzo negativo).
| Ejercicio
34: estudiar la evolución de una variable dinámica
aleatoria y con valores
{a,b,c} reforzada linealmente por una variable objetivo g cuyo valor depende de y según la tabla adjunta. A
tal efecto, supondremos que inicialmente fa=fb=fc=2,
despreciando la variación de las probabilidades durante cada B
pasos, de modo que tomaremos sucesivamente fk(t+B)
= fk(t) + (2gk-1)·fk(t)
. Representar gráficamente la evolución en el tiempo. Puede escenificarse el proceso asignando en cada paso los valores de y a miembros de la clase proporcionalmente a su probabilidad: inicialmente pueden asignarse según el valor de f hasta que se agoten los miembros, y a partir de ahí incrementar t en tantas unidades como miembros, asignándoles valores en el número entero más próximo a su proporción, de modo que cada miembro sume al valor de f de su valor la correspondiente cantidad 2g-1 . |
|
Objetivos:
- Escoger la mejor estrategia para la
consecución de un objetivo en relación a un conjunto de
escenarios.
- Simular la selección natural para escoger la mejor de las opciones.
- Calcular cuántas pruebas serán necesarias para encontrar con una cierta probabilidad una solución que esté dentro de un cierto porcentaje de las mejores.
- Escoger el mejor camino a través de una serie de bifurcaciones definidas por las decisiones a tomar y los eventos posibles.
Si podemos estimar la probabilidad de una variable objetivo (y) condicionada al escenario y la estrategia, P(y|s,e), así como la probabilidad de los distintos escenarios, P(s), supuestos independientes de las estrategias, aplicando el Teorema de Bayes obtendremos
P(y|e) = ∑s P(y|s,e)P(s) ,
lo cuál nos permitirà
evaluar qué estrategia tiene la máxima probabilidad de
satisfacer el objetivo.
Por su parte, si podemos estimar la posibilidad de una variable objetivo (y) condicionada al escenario para cada estrategia, πe(y|s), así como la posibilidad de los distintos escenarios, π(s), supuestos independientes de las estrategias, calcularemos para cada estrategia la posibilidad de cada valor de la variable objetivo,
Por su parte, si podemos estimar la posibilidad de una variable objetivo (y) condicionada al escenario para cada estrategia, πe(y|s), así como la posibilidad de los distintos escenarios, π(s), supuestos independientes de las estrategias, calcularemos para cada estrategia la posibilidad de cada valor de la variable objetivo,
πe(y) = maxs
min (πe(y|s),π(s))
lo cuál nos permitirá
evaluar qué estrategia conlleva la máxima posibilidad de
cada valor de la variable objetivo.
Ejercicio 35: encontrar la mejor estrategia para el siglo XXI entre (1) mantener el actual consumo energético, (2) reducir
Ejercicio 36: encontrar la
mejor estrategia para el siglo XXI entre las estrategias y en
relación a los escenarios descritos en el Ejercicio 35 para los
valores de la variable objetivo 0 (extinción de la humanidad),
0'5 (mera supervivencia) y 1 (felicidad), suponiendo que las
posibilidades de los escenarios son π(a)=1, π(b)=0'5 y π(c)=0'2 y las
posibilidades condicionales de los distintos valores de la variable
objetivo vienen dadas por las siguientes tablas:
Comparar la evaluación de las estrategias para los distintos
valores de la variable objetivo.
Ejercicio 35: encontrar la mejor estrategia para el siglo XXI entre (1) mantener el actual consumo energético, (2) reducir
| moderadamente el consumo
energético y (3) reducir
drásticamente el consumo energético, en relación a
los siguientes escenarios: (a) fuentes de energía actualmente
existentes, (b) descubrimiento de una fuente de energía
radicalmente nueva y (c) posibilidad de trasladarse a otro planeta
virgen con abundancia de recursos, suponiendo que las probabilidades de
los escenarios son P(a)=0'6, P(b)=0'3, P(c)=0'1 y que las
probabilidades
condicionales de conseguir el objetivo de que la humanidad viva
satisfactoriamente
vienen dadas por la tabla adjunta. |
|
|||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Actividad 37. Los algoritmos genéticos permiten simular la selección natural para escoger la mejor opción. Para ello se dan valores aleatorios a las variables de entrada, tanto las no controlables como las de control, modificando en cada paso las probabilidades de los valores de las variables de control en función de los resultados obtenidos. Ello puede hacerse de diversas formas. Por ejemplo, podría utilizarse un modelo de refuerzo lineal como el que se describe en la Actividad 35. Podría también tomarse en cada caso una probabilidad igual a la de la satisfacción obtenida. Y podría seleccionarse en cada paso un determinado porcentaje de los valores que han generado los mejores resultados.
Ejercicio 37: aplicar un algoritmo genético en las condiciones del Ejercicio 35, partiendo de 100 casos con estrategia 1, 100 casos con estrategia 2 y 100 casos con estrategia 3, y seleccionando en cada caso el 50% (o su parte entera) con mejores resultados (probabilidad de conseguir el objetivo). Para determinar de cada estrategia cuántos se encuentran en cada escenario, tomar la parte proporcional aproximando si es necesario con la parte entera y el resto mayor, o al azar en caso de restos iguales. En caso de empates con resultados seleccionables, tomar para cada estrategia la parte proporcional, aproximando del mismo modo si es necesario. ¿Cuántos habrán sobrevivido de cada estrategia después de 4 pasos?
Actividad 38. Para obtener por muestreo una solución que esté entre los 100p% mejores con una probabilidad del 100α%, deberemos calcular cual es la probabilidad de que entre n casos no haya ninguno que esté entre los 100p% mejores. Dado que la probabilidad de que un caso no esté entre los 100p% mejores es 1-p, y que los distintos casos deben considerarse independientes, la probabilidad de que entre n casos no haya ninguno que esté entre los 100p% mejores será (1-p)n. Por lo tanto, la probabilidad de que entre n casos haya alguno que esté entre los 100p% mejores será α=1-(1-p)n.
Ejercicio 38: ¿de qué tamaño deberá ser la muestra (con reemplazamiento) para garantizar con una probabilidad del 90% que el mejor resultado de la muestra esté entre el 5% de los mejores?
| Actividad
39. Un árbol de
decisión consiste en una bifurcación entre varias
decisiones posibles,
a raíz de cada una de las cuáles pueden producirse
distintos eventos
con determinadas probabilidades (o posibilidades), en respuesta a los
cuáles pueden a su vez tomarse distintas decisiones, y
así
sucesivamente, como se indica en las figuras adjuntas. Al final de cada
rama hay que evaluar su probabilidad (o posibilidad) así como
los
resultados obtenidos en relación a los objetivos previamente
definidos,
a fin de determinar una estrategia racional de decisiones sucesivas. Ejercicio 39: determinar la estrategia óptima de acuerdo con el árbol de decisión superior adjunto, donde los cuadrados indican bifurcación entre decisiones, se indica la probabilidad de cada evento, y al final de cada rama se indica el correspondiente resultado o probabilidad de satisfacción. Evaluar la expectativa de probabilidad de satisfacción después de cada decisión. Imaginar una posible aplicación de dicho arbol de decisión, o bien elaborar otro árbol de decisión para algún problema. Ejercicio 40: determinar la estrategia óptima de acuerdo con el árbol de decisión inferior adjunto, donde los cuadrados indican bifurcación entre decisiones, se indica la posibilidad de cada evento, y el final de cada rama se indica el correspondiente resultado o posibilidad de satisfacció. Evaluar la expectativa de posibilidad de satisfacción después de cada decisión. NOTA: recordad que: a) Las probabilidades condicionales se multiplican, y las probabilidades de opciones alternativas se suman. b) En relación a las posibilidades condicionales se toma el valor mínimo, y ante posibilidades de opciones alternativas se toma el máximo. |
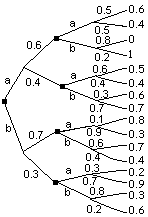 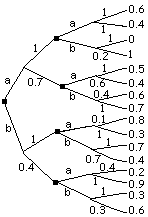 |
6. ESTUDIAR EL
COMPORTAMIENTO DE SISTEMAS
CAÓTICOS:
Objetivos:
- Entender cómo procesos deterministas pueden ser impredecibles.
- Estudiar sistemas caóticos generados por procesos
deterministas.
(con una medida definida sobre V,
para todo δ>0 existe ε>0 tal que si |x0-z0|<ε, entonces para todo número natural t, |ft(x0)-ft(z0)|<δ ),
para todo δ>0 existe ε>0 tal que si |x0-z0|<ε, entonces para todo número natural t, |ft(x0)-ft(z0)|<δ ),
de manera que si queremos predecir los
resultados finales con una precisión dada, simplemente deberemos
fijar las condiciones iniciales con una cierta precisión. Ahora
bien, pueden existir también determinadas condiciones iniciales x0
en las que ello no se cumple, es decir en las que una pequeña
variación de tales condiciones iniciales puede suponer una gran
variación de los resultados finales. En tal caso, diremos que
hay sensibilidad a las condiciones
iniciales, y los resultados finales serán impredecibles
ante pequeñas variaciones de las mismas a partir de x0
Actividad 41. Diremos que un sistema determinista es caótico si presenta sensibilidad generalizada a las condiciones iniciales y además presenta mezcla, de modo que desde cualquier condición inicial se llega tan cerca como se quiera de cualquier punto del conjunto de sus valores
(existe δ>0 tal que para todo
ε>0 existen un número natural t y z0cV tales que |x0-z0|<ε
y |ft(x0)-ft(z0)|>δ
).
Ejercicio 41: dado el proceso xt=(x0)t+1,
estudiar su sensibilidad a las condiciones iniciales.Actividad 41. Diremos que un sistema determinista es caótico si presenta sensibilidad generalizada a las condiciones iniciales y además presenta mezcla, de modo que desde cualquier condición inicial se llega tan cerca como se quiera de cualquier punto del conjunto de sus valores
( para todo δ>0, ε>0, x,zcV, existen x0cV y un
número natural t tal que |x0-x|<ε
y |ft(x0)-z|<δ
).
Puede demostrarse que hay sensibilidad
generalizada a las condiciones iniciales si el sistema presenta mezcla
y además el conjunto de puntos periódicos es denso en el
conjunto de sus valores
( para todo ε>0, zcV, existen x0cV
y un par de números naturales t'>t tales que |z-x0|<ε
y ft'(x0)=ft(x0)
)
o bien la función de
iteración f(x) es continua.
| Ejercicio
42: definimos el operador Shift mediante S(x)=2x si 0≤x<0'5,
S(x)=2x-1 si 0'5≤x<1, según se muestra en la figura adjunta.
En la figura inferior se indica la generación gráfica de
los sucesivos valores de xt. Si representamos
x en sistema binario (con 0s y 1s), para obtener S(x) deberemos
simplemente desplazar los bits (0s y 1s) un lugar a la izquierda y
descartar la parte entera si aparece. ¿Que valores de x
generarían una sucesión periódica? Comprobar que
el operador Shift cumple las propiedades de: a) Sensibilidad a las condiciones iniciales (para δ=0'01 en sistema binario). b) Densidad de puntos periódicos. c) Mezcla. A tal efecto dividiremos la clase en dos grupos,
|
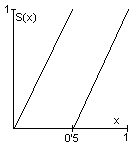 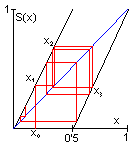 |