ANTERIOR

 LA CIENCIA

SIGUIENTE

Vamos ahora a analizar la naturaleza del conocimiento científico. En la página precedente hemos descrito superficialmente el papel que representa la ciencia en el conocimiento, pero hay muchos aspectos que necesitan ser aclarados. Para empezar vamos a particularizar en un ejemplo las consideraciones que hemos hecho hasta ahora sobre la ciencia, para dejar claro que estamos llamando ciencia exactamente a lo que cualquier científico entiende como tal.

A finales del siglo XVII, un mercader llamado Anton van Leeuwenhoek se especializó en la fabricación de microscopios, algunos de los cuales llegaron a tener una capacidad de doscientos aumentos. Con sus microscopios, Leeuwenhoek se dedicó a examinar y describir minuciosamente todo tipo de materiales. Descubrió los espermatozoides y los hematíes, y encontró en el agua estancada unos animálculos tan pequeños que eran invisibles al ojo humano. Sus observaciones y los experimentos de los investigadores que siguieron sus pasos llevaron, en un proceso que abarcó más de un siglo, al descubrimiento de los microorganismos y al desarrollo de la teoría celular. Sin ánimo de describir aquí todas las etapas de este proceso (lo cual sería muy largo e innecesario para nuestros fines), pero sin traicionar el hilo argumental básico, podríamos resumirlo y describirlo así:

Observemos cómo en un principio desconocía el concepto de microorganismo, unas experiencias me han llevado a introducirlo como un concepto empírico a posteriori que describe lo que estoy viendo, pero entonces mi razón elabora una teoría que trasciende esas experiencias y postula a priori que, en general, el mundo está lleno de microorganismos, a los que atribuye a priori una serie de características generales inducidas de dichas experiencias (datos sobre qué aspecto tienen, cómo se reproducen, de qué se alimentan, qué los mata, etc.). De este modo, cuando observo una nueva muestra con microorganismos, ahora es mi razón la que le dice a mi entendimiento que debe interpretar las intuiciones que recibe como correspondientes a microorganismos. Mi razón ha "creado" a priori el concepto racional de microorganismo inducida por mi entendimiento, pero ahora es mi entendimiento quien tiene que usar el concepto empírico de microorganismo por exigencia de mi razón. Al hacerlo así, estoy vinculando lo que experimento ahora sobre los microorganismos con las experiencias que en su día me llevaron a elaborar mi teoría sobre ellos.

Lo único esencialmente falso en este análisis es el uso de la primera persona. En la práctica, mi razón no tiene por qué deducir por sí misma todas sus teorías sobre el mundo, sino que puede aprenderlas de otras personas o de los libros (sin perjuicio de que yo pueda reproducir por mí mismo, si lo considero oportuno, los experimentos que han llevado a elaborar dichas teorías). Esto permite que una misma teoría racional, transmitida debidamente, pueda sintetizar las experiencias y las conclusiones de diversos investigadores. No obstante, de momento es más adecuada la primera persona, ya que todavía tenemos que analizar en qué medida mi experiencia me permite afirmar que en el mundo hay otros seres conscientes, aparte de mí.

A mediados del siglo XIX, Louis Pasteur estaba estudiando las fermentaciones, y demostró que estaban causadas por microorganismos. Más aún, cada fermentación (la del vino, la del vinagre, la de la cerveza, la del queso, etc.) la produce un microorganismo distinto. Huelga matizar lo que hemos de entender por "demostró": Pasteur trabajaba con cultivos en los que controlaba la presencia o ausencia de distintos microorganismos. Observó, por ejemplo, que si calentaba mosto hasta matar los microorganismos que contenía, ya no se producía la fermentación que lo convierte en vino, y que tampoco sucedía si después incorporaba al cultivo fermentos distintos de uno específico. Evidentemente, para un escéptico esto no prueba nada, pues las conclusiones de Pasteur exigían "suponer" que cualquier muestra de vino iba a comportarse igual que las de sus cultivos.

Sin embargo, Pasteur dedujo, en particular, que, calentando el vino ya fermentado, se impedía que éste se transformara a su vez en vinagre. Hasta entonces, la industria vinícola se resignaba a que, durante el proceso de envejecimiento, parte del vino se agriara sin que se supiera por qué, lo que ocasionaba pérdidas considerables. Pasteur recomendó a los industriales que calentaran los vinos a 55ºC antes de dejarlos envejecer (lo que ahora se llama pasteurización), con lo cual evitarían la fermentación acética. Aquí tenemos un ejemplo clarísimo de lo que es la ciencia. Los hechos empíricos son:

Por supuesto, si queremos considerar estas afirmaciones como empíricas, hay que entender que no hablamos de todas las muestras de vino posibles, sino únicamente de todas las muestras de vino con las que se ha hecho el experimento. De estos hechos empíricos, Pasteur indujo la siguiente teoría racional a priori:

Estas afirmaciones no son empíricas, sino racionales, ya que no hablan de ningún vino en concreto, sino del vino en general. No dicen lo que ha pasado, sino que predicen lo que va a pasar, y ninguna experiencia contiene información suficiente para avalar una predicción. Pasteur no afirmó nada de esto por capricho. Posiblemente, ni siquiera fue consciente de que había dado paso alguno al pasar del primer grupo de afirmaciones al segundo. Tan sólo consideró que no hay motivo para suponer que una muestra de vino va a comportarse de forma distinta a otra muestra de vino en idénticas circunstancias. Esto es la inducción empírica. No es una deducción lógica, ciertamente, pero obligó a los industriales del vino a dividirse en tres grupos:

No hace falta aclarar que toda la industria vinícola francesa adoptó en poco tiempo la propuesta de Pasteur. No se dio, que se sepa, ningún caso de escepticismo y, si hubo alguno de dogmatismo, no tardó nada en dar su brazo a torcer.

Tal y como indicábamos, el propósito de este ejemplo era convencer al lector de que no estamos afirmando nada original sobre la ciencia, sino únicamente analizándola en términos de la teoría del conocimiento. No vamos a hablar aquí sobre el método científico, es decir, de los requisitos que cabe exigir a una afirmación o teoría para que pueda considerarse científicamente comprobada. En la práctica, cualquier científico sabe si una teoría es seria o no lo es. Como ya hemos comentado, el "espíritu" del método científico es asegurar que sólo los hechos empíricos aboguen a favor o en contra de una teoría, y nunca los gustos, los sentimientos o los intereses de quienes la propugnan. Si un científico propone una teoría y se encuentra con que la experiencia la desmiente (más allá de lo que podría achacarse a errores experimentales), simplemente la descarta y busca otra, pero en ningún caso se obstina en amañarla o amañar los hechos para mantenerla contra viento y marea.

En particular, no vamos a analizar aquí el proceso de construcción de la ciencia, sino que nos vamos a ocupar únicamente de la ciencia "ya hecha". Aquí consideramos el concepto "ciencia" en su sentido más amplio: la ciencia recoge todo lo que sabemos sobre el mundo, desde que los polos magnéticos del mismo signo se repelen hasta que el asesinato es un delito penado por la justicia. Observemos que el uso que nuestra razón hace de ambas afirmaciones es el mismo: gracias a la primera sé a priori que, si acerco dos polos del mismo signo de un imán, experimentaré una fuerza de repulsión entre ellos; gracias a la segunda sé a priori que, si disparo a alguien en plena calle delante de un policía, éste me detendrá y me llevará a comisaría.

Sin embargo, para evitar dispersar nuestros argumentos, en nuestro propósito de comprender la naturaleza trascendental de la ciencia, vamos a centrarlos en la más básica de todas las ciencias: la física. Teóricamente, todos los principios científicos podrían deducirse de las leyes de la física, si bien en la práctica esto no es así, ya que tales deducciones deberían considerar una cantidad astronómica de datos y tener en cuenta una cantidad infinitamente mayor de relaciones entre ellos. No obstante, cuanto vamos a decir sobre la física puede adaptarse (simplificándose, de hecho) para cualquier otra rama de la ciencia.

Lo primero que hemos de entender es que la ciencia es una teoría formal. Para entender lo que esto significa vamos a establecer un paralelismo entre la ciencia y las matemáticas puras.

Podemos comparar una afirmación empírica, como "esta botella está vacía", con una afirmación como "2+2 = 4". No queremos decir que la segunda afirmación sea también empírica, sino que ambas tienen en común que tienen un significado, un contenido, empírico en el primer caso, intuitivo en el segundo, de modo que es dicho significado el que hace que sean verdaderas: para comprobar que la primera afirmación es verdadera recurrimos a la experiencia (miramos la botella y comprobamos que está vacía), mientras que para comprobar que la segunda es verdadera recurrimos a la intuición (pensamos "uno, dos... tres y cuatro") o incluso podemos recurrir también a la experiencia, aunque sepamos que la experiencia concreta que consideremos es irrelevante (por ejemplo, extiendo dos dedos de mi mano izquierda, otros dos de mi mano derecha, miro ambas manos, y compruebo que estoy viendo cuatro dedos).

Consideremos ahora una afirmación como "hay una botella en el armario". Si hablamos de un armario cerrado, esta afirmación no puede comprobarse empíricamente. Si abro el armario para comprobarlo, estoy comprobando que ahora hay una botella en el armario, pero no que estaba ahí cuando el armario estaba cerrado. Lo mismo es válido, por otro motivo, para "las botellas de cristal son frágiles". Ésta no es comprobable empíricamente porque hace referencia a todas las botellas de cristal posibles, y no puedo comprobar empíricamente que todas ellas son frágiles. ¿Qué afirmaciones matemáticas podrían considerarse equivalentes a estas dos afirmaciones racionales?

A finales del siglo XIX, el matemático Georg Cantor construyó una teoría de cardinales infinitos. Con dicha teoría, es posible asignar un número de elementos (un cardinal) no sólo a los conjuntos finitos, sino también a los conjuntos infinitos, y Cantor probó que los cardinales infinitos (los números que permiten contar a los conjuntos infinitos) pueden ordenarse en la sucesión de los alephs:


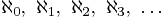
de modo que los conjuntos infinitos más pequeños tienen aleph-cero elementos, los menores entre los que tienen más de aleph-cero elementos tienen aleph-un elementos, etc. Podemos comparar la afirmación racional "hay una botella en el armario" con la fórmula matemática 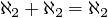. Los matemáticos discuten sobre si una afirmación como ésta tiene un contenido intuitivo, análogo al que tiene la fórmula "2+2 = 4", o si, por el contrario, carece de significado. No necesitamos entrar aquí en esta discusión, pues lo único que importa es que ningún matemático aceptará que alguien admita como evidente la afirmación 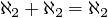. Todos los matemáticos coinciden en que esta fórmula requiere ser demostrada, y el único contexto en el que puede ser demostrada es en el seno de la llamada teoría de conjuntos.

La teoría de conjuntos consiste en una colección de axiomas en los que aparecen las nociones de conjunto y de pertenencia entre conjuntos. Estas nociones no se definen, sino que simplemente se especifica que vamos a hablar de unos objetos llamados conjuntos y que, dados dos conjuntos, puede suceder que uno pertenezca al otro o que no pertenezca. Son los axiomas (y no unas inexistentes e imposibles definiciones) los que determinan qué podemos afirmar sobre los conjuntos y la pertenencia. En esencia, los axiomas de la teoría de conjuntos vienen a decir: "Los conjuntos (sean lo que sean) y la relación de pertenencia (consista en lo que consista) cumplen esto y lo otro". Por ejemplo, uno de los axiomas dice concretamente: "Existe un conjunto al cual no pertenece ningún conjunto", otro afirma: "Dados dos conjuntos, existe un tercero al que pertenecen únicamente los dos conjuntos dados".

Es obvio que estas afirmaciones, mientras no especifiquemos qué significa "conjunto" y qué significa "pertenecer", no significan nada, pero ello no impide que, a partir de estos dos conceptos elementales, se puedan definir muchos más (números, funciones, rectas, planos, integrales, cardinales infinitos, etc.) y que a partir de los axiomas de la teoría de conjuntos se puedan demostrar todos los teoremas matemáticos. En particular, a partir de los axiomas de la teoría de conjuntos puede deducirse lógicamente que .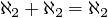

Observemos que, en principio, para que esta fórmula tenga sentido en el seno de la teoría de conjuntos es necesario definir 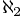, al igual que la suma de cardinales, pero dichas definiciones no atribuyen realmente un significado a 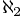porque contienen otros conceptos matemáticos que a su vez están definidos en función de otros y, si rastreamos hasta el final las definiciones, acabamos inevitablemente en los conceptos de "conjunto" y "pertenencia" que no hemos definido. Esto no quiere decir que la fórmula 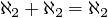no signifique nada, sino únicamente que su posible significado es irrelevante en el proceso de demostración, y esto es precisamente lo que queremos decir cuando afirmamos que la teoría de conjuntos es una teoría formal: que no tiene en cuenta el posible contenido de las afirmaciones, sino sólo su forma. Quizá un ejemplo sencillo aclare este punto. He aquí un razonamiento formal cuya naturaleza es exactamente la misma que la de cualquier otro razonamiento formal de cualquier teoría formal:

Es un razonamiento correcto aunque no signifique nada. De hecho, podría significar algo; bastaría dar un sentido a las tres palabras inventadas que aparecen. Si les damos un sentido con el cual las dos premisas resulten verdaderas, podemos estar seguros de que la conclusión será verdadera, pero lo esencial es que esto es así independientemente de que las tres afirmaciones signifiquen algo o no signifiquen nada.

Los matemáticos que piensan que la matemática transfinita tiene un significado intuitivo, piensan que, en particular, lo tienen las nociones de "conjunto" y "pertenencia",  y que los axiomas expresan afirmaciones intuitivamente verdaderas sobre estos conceptos, lo que, a su vez, hace que todos los teoremas deducidos lógicamente a partir de los axiomas son también intuitivamente verdaderos (aunque nuestra intuición no sea capaz de mostrárnoslo directamente, al contrario de lo que sucede con "2+2 = 4").

Observemos también que lo mismo podríamos hacer con la fórmula "2+2 = 4": esta fórmula también puede ser demostrada a partir de los axiomas de la teoría de conjuntos, con lo cual estamos prescindiendo completamente de su significado intuitivo. La diferencia es que aquí tenemos las dos opciones: podemos comprobar que es cierta observando que lo que significa es verdad, o bien demostrándola formalmente, es decir, prescindiendo de su significado. Insistimos en que un niño de diez años que mire sus dedos para concluir que "2+2 = 4" sabe que 2+2 = 4 exactamente en el mismo sentido y con la misma profundidad que lo sabe un matemático profesional. El matemático conoce otros caminos para llegar a la misma conclusión, pero la conclusión no deja, por ello, de ser la misma. En el caso de 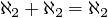, tanto si tiene un significado intuitivo como si no, lo cierto es que no podemos confiar en nuestra intuición para determinar si esta afirmación es verdadera o falsa, por lo que lo único que podemos hacer es justificarla indirectamente, por deducción a partir de unos axiomas que podrían ser intuitivamente verdaderos, aunque lo cierto es que, a la hora de la verdad, esto no afecta en nada.

El mismo problema se nos presenta cuando queremos decidir si es verdadera o no una afirmación como "el Sol está hecho fundamentalmente de hidrógeno y de helio". Ahora lo que nos falla no es la intuición, sino la experiencia. Ninguna experiencia nos muestra esto directamente. A lo sumo podemos analizar el espectro de la luz solar y observar las rayas oscuras que presenta. Uniendo esto a una teoría atómica y a unas pruebas de laboratorio sobre los espectros de los diferentes elementos químicos, deducimos lógicamente que el Sol está hecho fundamentalmente de hidrógeno y de helio. Una diferencia clara entre los razonamientos matemáticos (en el seno de la teoría de conjuntos) y los razonamientos físicos es que los primeros parten de un inventario cerrado de axiomas, mientras que los segundos parten de dos clases de axiomas: los principios a priori proporcionados por la ciencia (las leyes de la física), que también constituyen un inventario cerrado (o, al menos, lo constituirían si dispusiéramos ya de una física completa) y los hechos a posteriori proporcionados por la experiencia, que son potencialmente infinitos. En el ejemplo que estamos considerando necesitamos, por una parte, una teoría atómica a priori que nos indique la relación entre la composición de una estrella y la estructura de su espectro luminoso y, por otra parte, las experiencias a posteriori que nos indiquen cuál es concretamente el espectro del Sol y cuáles son los espectros característicos de los distintos elementos químicos. Teóricamente, éstos últimos deberían poder predecirse también a priori.

Como en el caso de las matemáticas, es posible definir unos conceptos físicos en función de otros. Por ejemplo, podemos definir una estrella como una masa gaseosa en cuyo seno se producen reacciones nucleares de fusión. Sin embargo, también como en el caso de las matemáticas, si vamos rastreando las definiciones, acabaremos necesariamente con conceptos que no pueden ser definidos en términos de otros más elementales y, lo que es más importante, que tampoco pueden ser definidos en términos de la experiencia. Pensemos, por ejemplo, en el concepto físico de "masa". Podríamos dar una "definición" empírica de la masa de un cuerpo en términos de una balanza: ponemos el cuerpo en el platillo de una balanza y su masa (en kg) es igual al número de litros de agua que hay que poner en el otro platillo para que la balanza se equilibre. Es fácil encontrar mil razones por las que esta definición es una chapuza, pero no merece la pena que nos esmeremos más con el ejemplo, porque cualquier otra "definición" posible compartirá con ésta deficiencias esenciales. Por ejemplo, esta "definición" no puede usarse para deducir que dos cuerpos cualesquiera se atraen con una fuerza directamente proporcional a sus masas. Al contrario, son principios como éste los que permiten justificar que, en ciertos casos particulares, con una balanza y agua podemos medir la masa de un objeto.

La única forma de entender el concepto de "masa" acorde con el uso que la física hace de él es comprender que la física parte de que en el mundo hay objetos (partículas elementales, o quarks, o supercuerdas, o lo que los físicos estimen oportuno), de entre los cuales, algunos tienen una propiedad que llamamos masa, (no todos: los electrones sí, los fotones no) la cual está determinada por un número no negativo salvo la elección de una unidad. No es necesario (ni posible) definir qué es la masa. Simplemente, ésta aparecerá en algunas de las leyes físicas que determinan el comportamiento del mundo. A su vez, estas leyes proporcionarán diversos métodos empíricos para calcular la masa de un objeto. (Aquí usamos el ejemplo de la masa por claridad, siguiendo la política de no entrar innecesariamente en tecnicismos físicos, pero hemos de advertir que sí que es posible dar una definición de masa, o de carga eléctrica, etc., como sucede, de hecho, en la teoría de cuerdas, donde estos conceptos se definen a partir de otros más abstractos y no definibles en la teoría, lo cual no altera la esencia de lo que estamos diciendo, sino que únicamente nos obliga a sustituir en nuestra discusión la palabra "masa" por términos más abstractos, no definibles en la propia teoría, como el de "cuerda" y los atributos que permiten considerar una cuerda como una vibración dotada de los atributos propios de una cuerda vibrante.)

Los matemáticos no tienen ningún nombre estándar para referirse a la totalidad de los conjuntos, porque este concepto presenta muchos problemas técnicos, pero, si en lugar de pensar en la axiomatización de la teoría de conjuntos nos restringimos a la axiomatización de la geometría, entonces podemos comparar el concepto de "mundo" con el de "espacio". Los físicos dicen "en el mundo hay partículas elementales" igual que los geómetras (axiomáticos) dicen "en el espacio hay puntos, rectas y planos". El mundo es simplemente "aquello de lo que habla la física" igual que el espacio es simplemente "aquello de lo que habla la geometría". No es necesario (ni posible) definir el mundo a la hora de fundamentar la física, igual que no es necesario (ni posible) definir el espacio a la hora de fundamentar la geometría.

En resumen, afirmamos que la física, entendida como el producto de la razón cuando trata de interpretar lo más básico de nuestras experiencias, es exactamente el contenido de un libro de física. La física cabe en un libro de física, un libro que grosso modo, empezará explicitando sin definición los conceptos que van a usarse en él para describir el mundo: quarks, fotones, masa, spin, encanto, gravitación, fuerza nuclear fuerte, espacio, tiempo, etc., y a continuación explicitará las leyes que regulan el comportamiento del mundo en términos de estos conceptos básicos y de otros definidos a partir de ellos. Dicho libro también incluirá datos concretos (empíricos) sobre el mundo, como la masa del Sol, la distancia del Sol a la Tierra, etc. Todo hecho empírico que no pueda justificarse a priori en el seno de la teoría física, será formalmente un axioma dentro de dicha teoría.

Naturalmente, es posible escribir libros de "física" mutuamente contradictorios entre sí. Así como la geometría tridimensional euclídea se distingue de las demás geometrías formales en que es la única a la que podemos dar un contenido intuitivo, es decir, es la única tal que a todas sus afirmaciones, en principio formales, se les puede atribuir un contenido intuitivo de forma que resultan verdaderas, la física es (o pretende ser) la única teoría física formal, no susceptible de que todas sus afirmaciones formales admitan una interpretación empírica que resulte verdadera, sino susceptible de que algunas de sus afirmaciones formales admitan una interpretación empírica que resulte verdadera, pero de tal modo que todas las afirmaciones empíricas (todas las de naturaleza física, o todas en general si cambiamos "física" por "ciencia") puedan obtenerse como interpretaciones empíricas de afirmaciones físicas, en principio formales, adecuadas. (El matiz "o pretende ser" sólo hace referencia a lo que ya hemos discutido sobre qué es racional y qué no lo es.)

Del mismo modo que sólo una estrecha franja de frecuencias del espectro electromagnético tiene una interpretación intuitiva (el espectro visible), en general, sólo una parte de los hechos racionales tiene una interpretación empírica. El concepto racional (físico) de Sol es más amplio que lo que cabe en cualquier experiencia, porque es una síntesis de todas las experiencias relativas al Sol que incorpora además los hechos a priori necesarios para que dicha síntesis pueda realizarse. Como afirmaciones físicas, "Hoy a las doce del mediodía el Sol brilla en el cielo", "el Sol contiene helio" y "el Sol broncea la piel" son de la misma naturaleza: son tres afirmaciones formales que se deducen de las leyes de la física, pero empíricamente son muy distintas: la primera tiene un contenido empírico, puedo comprobarla empíricamente; la segunda carece de contenido empírico directo, su relación con la experiencia es que puede deducirse de ciertas experiencias e implica a su vez otras experiencias; la tercera está a mitad de camino entre las otras dos: puede comprobarse empíricamente en casos particulares, si bien contiene una componente a priori (su universalidad, el hecho de que el Sol siempre broncea la piel expuesta al mismo) que no puede "leerse" de ninguna experiencia.

Sin embargo, no tendría ningún fundamento que, en algún sentido, consideráramos "más verdadera" la primera afirmación que cualquiera de las otras dos. Insistimos en que, desde el punto de vista de la física (desde un punto de vista racional), las tres afirmaciones son de la misma naturaleza. Tan cierto es que estoy viendo brillar el Sol sobre mi cabeza como que el Sol contiene helio. Podemos comparar esta situación con la información que obtenemos en la representación de una obra de teatro: conocemos ciertos hechos porque los vemos suceder en la escena, mientras que otros los conocemos indirectamente, porque los personajes afirman que han sucedido fuera de la escena, pero todos ellos son igual de reales en relación con el argumento de la obra.

Del mismo modo que una afirmación racional (física) puede carecer de un contenido empírico directo o tener sólo parcialmente contenido empírico, lo mismo sucede con los conceptos racionales. Ya hemos explicado que un concepto como el de "Sol" es no meramente un concepto empírico, es decir, unas reglas que permiten a nuestro entendimiento aplicarlo como parte de la descripción de ciertas experiencias (lo que hacemos cuando decimos "eso es el Sol"), sino que, en toda su generalidad, es un concepto racional, un concepto integrado en una teoría formal sobre el mundo algunas de cuyas afirmaciones admiten una interpretación empírica que puede confirmarlas o refutarlas; sin embargo, también puede haber conceptos racionales que carezcan completamente de interpretación empírica.

Aquí podemos distinguir grados. Por ejemplo, el concepto de "dinosaurio" podría considerarse empírico en el sentido de que nuestro entendimiento podría aplicarlo para describir una experiencia (si estuviéramos ante un dinosaurio, nuestro entendimiento podría decir "eso es un dinosaurio"); pero la ciencia nos dice que los dinosaurios se han extinguido, por lo cual, en la práctica, nunca tendremos una experiencia susceptible de ser descrita con el concepto de dinosaurio, y todas las afirmaciones racionales sobre dinosaurios serán necesariamente inferidas de otras afirmaciones empíricas en las que no aparecerá el concepto "dinosaurio", aunque sí otros conceptos relacionados, como el de "hueso de dinosaurio". El mero hecho de aplicar el concepto de "hueso de dinosaurio" a un objeto presupone ya una inferencia desde un hecho empírico "esto es un hueso" hasta un hecho racional formal "el hueso perteneció a un dinosaurio".

No obstante, la razón, en su descripción del mundo, puede manejar conceptos puramente formales, en el sentido de que no queden fuera de la experiencia por el mero hecho de haber nacido en el momento inadecuado. Es el caso, por ejemplo, de las llamadas partículas virtuales: la mecánica cuántica afirma que el producto del tiempo necesario para detectar una partícula por la energía que ésta contiene ha de ser mayor o igual que una cierta constante, de modo que si una partícula se crea de la nada y desaparece en la nada en un tiempo suficientemente breve, será imposible detectarla empíricamente; sin embargo, esto no significa que no exista; al contrario, las interacciones entre partículas se explican en términos de intercambios de partículas virtuales. Los físicos usan "virtual" como opuesto a "real", pero aquí usan "virtual" en un sentido distinto al que nosotros damos a la palabra (lo usan en el sentido de "no observable empíricamente"). Para nosotros, las partículas virtuales son tan reales como las partículas reales, en el sentido de que tan pertinente es hablar de unas como de las otras a la hora de describir racionalmente el mundo. (Insistimos en que con esto no contradecimos el criterio de los físicos, sino que únicamente estamos dando a la palabra "real" un sentido técnico adecuado para la teoría del conocimiento distinto del sentido técnico que le dan los físicos.)

Los conceptos de "realidad" o "verdad" son conceptos formales a priori con los que expresamos los contrastes entre una afirmación y los datos que nos proporciona la intuición, el entendimiento o la razón. (Gramaticalmente, usamos "real" cuando el sujeto es un sustantivo y "verdadero" cuando el sujeto es una afirmación, pero el sentido es el mismo. Los adverbios "realmente" y "verdaderamente" son sinónimos.) Según con qué contrastemos, podemos llegar a conclusiones distintas:

En cambio, no podemos explicar qué queremos decir si afirmamos que algo es trascendentalmente real, es decir, que "está realmente ahí fuera" y que el concepto que tenemos de ello se corresponde con lo que realmente es. Yo puedo decir que la mesa que tengo ante mí es intuitivamente real, empíricamente real y racionalmente real, porque la puedo ver y tocar, lo cual garantiza que es intuitivamente real, y mi entendimiento me dice que si puedo ver y tocar una mesa es porque ante mí hay una mesa empíricamente real, y mi razón me dice que si tengo la experiencia de una mesa, es porque en el mundo existe una mesa situada ante mí, luego la mesa es racionalmente real; ahora bien, si estuviera conectado a Matrix, esa mesa no sería trascendentalmente real. Seguiría siendo intuitiva, empírica y racionalmente real, en el sentido de que mi intuición, mi entendimiento y mi razón estarían actuando correctamente, sin errores, pero la mesa sólo sería ese concepto que me he formado a partir de mis percepciones, existiría, ciertamente, una realidad trascendente, a la que pertenece el ordenador gigante que contiene a Matrix, pero en esa realidad trascendente no habría ninguna mesa. Es fácil explicar lo que significa que algo empíricamente real no sea trascendentalmente real, lo cual basta para que afirmar que algo es trascendentalmente real significa algo, a pesar de que no estemos en condiciones, no ya de saber si es así o no, sino siquiera de explicar lo que significa.

Podemos expresar esto diciendo que el mundo, el mundo racionalmente real que conocemos, es trascendentalmente ideal, es decir, que, en principio, es únicamente una construcción mental, una teoría formal construida a priori a partir de nuestras experiencias. Ahora bien, nada de esto niega la posibilidad (metafísica) de que ese mismo mundo trascendentalmente ideal se corresponda con (describa) una realidad trascendentalmente real. En otras palabras, es posible que la ciencia esté describiendo realmente, fielmente, "lo que hay", a pesar de que ni siquiera seamos capaces de explicar qué entendemos por "lo que hay". Más adelante hemos de volver sobre esto.

El entendimiento y la razón

Índice

Sobre el concepto de sustancia