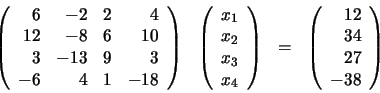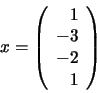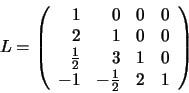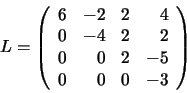6.1.3 Eliminación gaussiana básica

Next: 6.1.4 Método de Gauss-Jordan Up: 6.1 Métodos de resolución Previous: 6.1.2 La factorización LU

6.1.3 Eliminación gaussiana básica

Ilustraremos el método de Gauss aplicando el procedimiento a un sistema de cuatro ecuaciones con cuatro incógnitas:

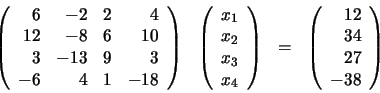$\begin{displaymath}\begin{array}{llll} \left( \begin{array}{rrrr} 6 & -2 & 2 ... ...ay}{r} 12 \\ 34 \\ 27 \\ -38 \end{array} \right) \end{array}\end{displaymath}$

(58)

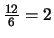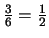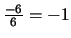En el primer paso, multiplicamos la primera ecuación por $\frac{12}{6}=2$ y la restamos a la segunda, después multiplicamos la primera ecuación por $\frac{3}{6}=\frac{1}{2}$ y la restamos a la tercera y finalmente multiplicamos la primera ecuación por $\frac{-6}{6}=-1$ y la restamos a la cuarta. Los números 2, 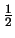$\frac{1}{2}$ y -1 son los multiplicadores del primer paso del proceso de eliminación. El número 6 es el elemento pivote de este primer paso y la primera fila, que no sufre modificación alguna, se denomina fila pivote. El sistema en estos momentos tiene el siguiente aspecto:

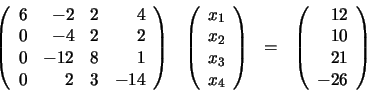$\begin{displaymath}\begin{array}{llll} \left( \begin{array}{rrrr} 6 & -2 & 2 ... ...ay}{r} 12 \\ 10 \\ 21 \\ -26 \end{array} \right) \end{array}\end{displaymath}$

(59)

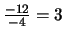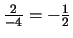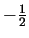En el siguiente paso del proceso, la segunda fila se emplea como fila pivote y -4 como elemento pivote. Aplicamos del nuevo el proceso: multiplicamos la segunda fila por $\frac{-12}{-4}=3$ y la restamos de la tercera y después multiplicamos la segunda fila por $\frac{2}{-4}=-\frac{1}{2}$ y la restamos a la cuarta. Los multiplicadores son en esta ocasión 3 y $-\frac{1}{2}$ y el sistema de ecuaciones se reduce a:

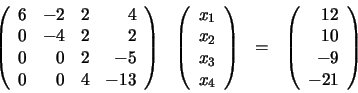$\begin{displaymath}\begin{array}{llll} \left( \begin{array}{rrrr} 6 & -2 & 2 ... ...ay}{r} 12 \\ 10 \\ -9 \\ -21 \end{array} \right) \end{array}\end{displaymath}$

(60)

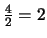El último paso consiste en multiplicar la tercera ecuación por $\frac{4}{2}=2$ y restarla a la cuarta. El sistema resultante resulta ser:

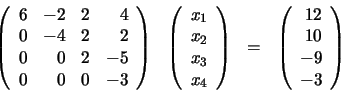$\begin{displaymath}\begin{array}{llll} \left( \begin{array}{rrrr} 6 & -2 & 2 ... ...ray}{r} 12 \\ 10 \\ -9 \\ -3 \end{array} \right) \end{array}\end{displaymath}$

(61)

El sistema resultante es triangular superior y equivalente al sistema original (las soluciones de ambos sistemas coinciden). Sin embargo, este sistema es fácilmente resoluble aplicando el algoritmo de sustitución regresiva explicado en el apartado 6.1.1. La solución del sistema de ecuaciones resulta ser:

$\begin{displaymath}x = \left( \begin{array}{r} 1 \\ -3 \\ -2 \\ 1 \end{array} \right) \end{displaymath}$

Si colocamos los multiplicadores utilizados al transformar el sistema en una matriz triangular inferior unitaria (L) ocupando cada uno de ellos la posición del cero que contribuyó a producir, obtenemos la siguiente matriz:

$\begin{displaymath}L = \left( \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 2 & 1 & 0... ...& 3 & 1 & 0 \\ -1 & -\frac{1}{2} & 2 & 1 \end{array}\right) \end{displaymath}$

Por otra parte, la matriz triangular superior (U) formada por los coeficientes resultantes tras aplicar el algoritmo de Gauss (ecuación 61), es:

$\begin{displaymath}L = \left( \begin{array}{rrrr} 6 & -2 & 2 & 4 \\ 0 & -4 &... ... 2 \\ 0 & 0 & 2 & -5 \\ 0 & 0 & 0 & -3 \end{array}\right) \end{displaymath}$

Estas dos matrices nos dan la factorización LU de la matriz inicial de coeficientes, A, expresada por la ecuación (58):

$\begin{displaymath}\begin{array}{llll} \left( \begin{array}{rrrr} 6 & -2 & 2 ... ...0 & 2 & -5 \\ 0 & 0 & 0 & -3 \end{array} \right) \end{array}\end{displaymath}$

**Figure:** Implementación del algoritmo de eliminación gaussiana.
$\begin{figure} \begin{center} \begin{tabular}{\vert l\vert} \hline \\ ~~~~~... ...$a_{ij}$ ) \\ ~ \\ \hline \end{tabular} \end{center} \protect\end{figure}$

En la figura (12) se muestra un algoritmo en pseudocódigo para llevar a la práctica el proceso básico de eliminación gaussiana que acabamos de describir. En este algoritmo se supone que todos los elementos pivote son distintos de cero.

Next: 6.1.4 Método de Gauss-Jordan Up: 6.1 Métodos de resolución Previous: 6.1.2 La factorización LU

Wladimiro Diaz Villanueva
1998-05-11