

Next: 6.1.2 La factorización LU
Up: 6.1 Métodos de resolución
Previous: 6.1 Métodos de resolución
6.1.1 Sistemas fáciles de resolver
Analizaremos previamente un sistema que sea fácil de
resolver. Por ejemplo, supongamos que la matriz A de
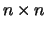 presenta estructura diagonal, es decir, todos los componentes
distintos de cero se encuentran sobre la diagonal principal. El
sistema de ecuaciones (43) toma por tanto la forma:
presenta estructura diagonal, es decir, todos los componentes
distintos de cero se encuentran sobre la diagonal principal. El
sistema de ecuaciones (43) toma por tanto la forma:
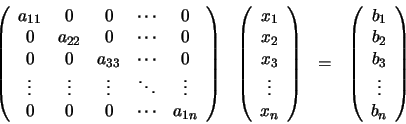 |
(45) |
En este caso el sistema se reduce a n ecuaciones simples y la
solución es:
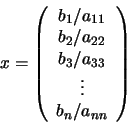 |
(46) |
Continuando con la búsqueda de sistemas con soluciones
fáciles, supongamos ahora que A tiene una estructura
triangular inferior, es decir, todos los elementos de Adistintos de cero se sitúan bajo la diagonal principal:
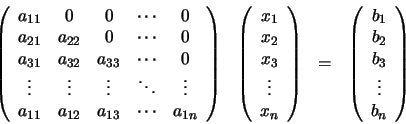 |
(47) |
Es fácil ver que el valor de x1 se obtiene directamente a partir
de la primera ecuación. Sustituyendo el valor conocido de x1 en
la segunda ecuación es posible obtener el valor de x2.
Procediendo de la misma forma para el resto de las ecuaciones, es
posible obtener todos los valores x1 , x2, x3, ...,
xn uno tras otro y en ese orden. El algoritmo formal para
encontrar la solución se denomina sustitución progresiva y se
puede expresar como:
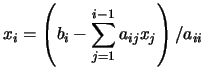 |
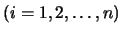 |
|
(48) |
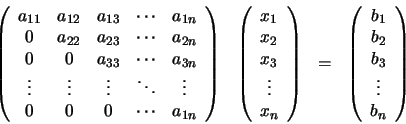
Se puede emplear el mismo razonamiento para el caso en que la
estructura de la matriz A sea triangular superior. En este
caso el sistema matricial adopta la forma:
 |
(49) |
y es posible obtener las soluciones en el orden xn, xn-1,
..., x1, empleando en este caso una modificación del algoritmo
expresado por la ecuación (48) y que denominados
algoritmo de sustitución regresiva:
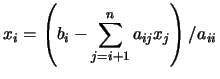 |
 |
|
(50) |
Como es lógico, los métodos descritos se pueden aplicar a todos
aquellos sistemas que se pueden convertir en un sistema triangular
permutando filas y columnas de forma adecuada.


Next: 6.1.2 La factorización LU
Up: 6.1 Métodos de resolución
Previous: 6.1 Métodos de resolución
Wladimiro Diaz Villanueva
1998-05-11
![]() presenta estructura diagonal, es decir, todos los componentes
distintos de cero se encuentran sobre la diagonal principal. El
sistema de ecuaciones (43) toma por tanto la forma:
presenta estructura diagonal, es decir, todos los componentes
distintos de cero se encuentran sobre la diagonal principal. El
sistema de ecuaciones (43) toma por tanto la forma: