Figure:
Caso subsónico: La perturbación se propaga, respecto del sistema de referencia laboratorio,
con una velocidad 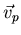 (
(
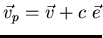 ). Dicha perturbación
se puede propagar en todas direcciones y, eventualmente, alcanzará cualquier punto de la región que
contiene el gas.
). Dicha perturbación
se puede propagar en todas direcciones y, eventualmente, alcanzará cualquier punto de la región que
contiene el gas.
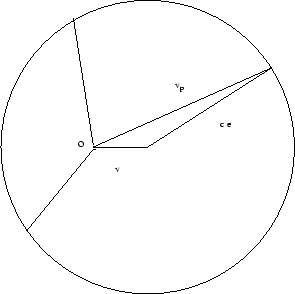 |
Figure:
Caso supersónico: La perturbación se propaga, respecto del sistema de referencia laboratorio,
con una velocidad 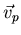 (
(
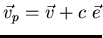 ). Dicha perturbación
se propaga dentro de un cono de semiapertura
). Dicha perturbación
se propaga dentro de un cono de semiapertura 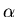 :
:
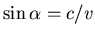 .
.
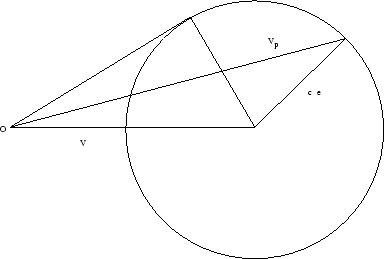 |
Figure 6:
Dominio de dependencia de P (izquierda) y rango de influencia de Q (derecha)
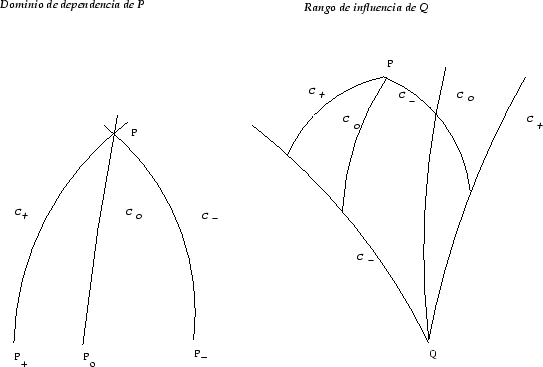 |
Figure 7:
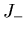 de compresión:
de compresión: 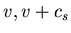 aumentan.
(Forward-facing compression wave)
aumentan.
(Forward-facing compression wave)
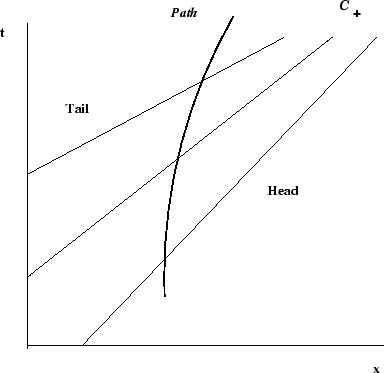 |
Figure 8:
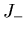 de rarefacción:
de rarefacción: 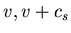 disminuyen.
(Forward-facing expansion wave)
disminuyen.
(Forward-facing expansion wave)
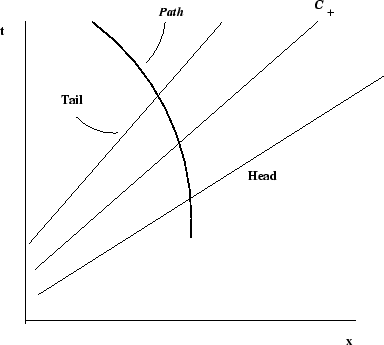 |
Figure 9:
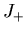 de compresión:
de compresión: 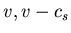 disminuyen.
(Backward-facing compression wave)
disminuyen.
(Backward-facing compression wave)
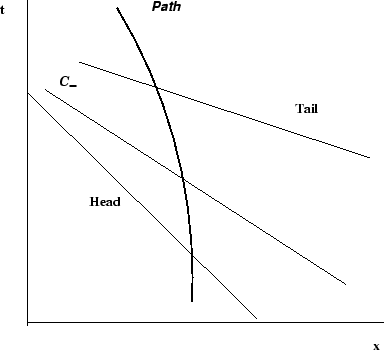 |
Figure 10:
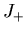 de rarefacción:
de rarefacción: 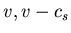 aumentan.
(Backward-facing expansion wave)
aumentan.
(Backward-facing expansion wave)
 |

