2.1 Dinámica de fluidos: Introducción

$\Longrightarrow$ Un fluido simple (a diferencia de un sólido) es un material en el que las posiciones relativas de sus elementos cambian mucho al aplicar una fuerza, aunque ésta sea pequeña en magnitud.

Rango interacción molecular (que no forman un enlace químico): $d_0 \approx 3-4 \times 10^{-8} cm.$

En sustancias compuestas por moléculas simples, la distancia intermolecular promedio, en la fase gaseosa, es del orden de $10 d_0$.

$\Longrightarrow$ La dinámica de fluidos $\Longrightarrow$ Evolución de magnitudes macroscópicas, i.e., magnitudes promediadas en elementos de volumen de tamaño $l \gg d_0$.

Supondremos que el comportamiento macroscópico del fluido es el mismo que si éste fuera perfectamente continuo $\Longrightarrow$ Las magnitudes que caracterizan el fluido serán funciones de $(\vec{r}, t)$

$\Longrightarrow$ Descripción euleriana: Cómo varian las propiedades del fluido, con el paso del tiempo, en un punto fijo del espacio.

$\Longrightarrow$ Descripción lagrangiana: Cómo varian las propiedades de una partícula del fluido en su movimiento.

$\Longrightarrow$ Líneas de corriente: $\vec{r}=\vec{r}(\lambda)$

$\Longrightarrow$ Curvas integrales del campo de velocidades:

$${ \frac{d\vec{r}}{d\lambda} = \vec{v} \left( \vec{r}(\lambda),t \right) }$$ $\Longleftrightarrow$ $${ \frac{d x}{v_x (\vec{r},t)} = \frac{d y}{v_y (\vec{r},t)} = \frac{d z}{v_z (\vec{r},t)} (= d\lambda) }$$

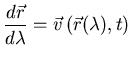
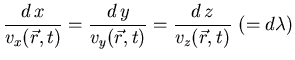
$\Longrightarrow$ Flujo estacionario $\Longrightarrow$ El campo de velocidades no depende del tiempo

$\Longrightarrow$ Las líneas de corriente son las mismas en todo instante.

$\Longrightarrow$ Las líneas de corriente coinciden con las trayectorias

de las partículas de fluido.