3.3.3 Physical solutions

The class of all weak solutions is too wide in the sense that there is no uniqueness for the IVP

The numerical methods should guarantee convergence to the physically admisible solution. This is the limit solution, when $\varepsilon\rightarrow 0$ of the ``viscous version" of system (84)

$$\frac{\partial {\bf u}}{\partial t} + \sum_{j=1}^{d} \frac{\... ...silon \sum_{j=1}^{d} \frac{\partial^2 {\bf u}}{\partial x_j^2}$$ (93)

Mathematically, it is characterized by the so-called entropy condition (in the language of fluids, the condition that the entropy of any fluid element should increase when running into a discontinuity)

The characterization of the entropy-satisfying solutions for scalar equations follows Oleinik (1963), whereas for systems of conservation laws it has been developed by Lax (1972).

Entropy condition (for scalar equations): $u(x,t)$ is the entropy solution if all discontinuities have the property that

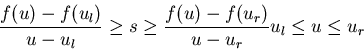$$\frac{f(u)-f(u_l)}{u-u_l}\ge s \ge \frac{f(u)-f(u_r)}{u-u_r} u_l \le u \le u_r$$ (94)